Cohomologie de De Rham - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, la cohomologie de de Rham est un outil de topologie différentielle, c'est-à-dire adapté à l'étude des variétés différentielles. Il s'agit d'une théorie cohomologique basée sur des propriétés algébriques des espaces de formes différentielles sur la variété. Elle porte le nom du mathématicien Georges de Rham. Le théorème de de Rham affirme que la cohomologie de de Rham d'une variété différentielle est la cohomologie à coefficients réels de l'espace topologique sous-jacent.
Définitions
Soit M une variété différentielle, et Ωp(M) l'ensemble des formes différentielles ω de degré p sur M. Cet ensemble a une structure de fibré vectoriel sur M.
Soit dp l'opérateur de différentiation extérieure sur les formes différentielles de degré p :

qui associe à la forme différentielle ω de degré p sa dérivée extérieure dω, forme différentielle de degré p + 1.
On note dω la dérivée extérieure de ω quand on ne veut pas préciser son degré; il faut alors sous-entendre dpω où p est le degré de ω.
Formes fermées, formes exactes
Lorsque dω = 0, on dit que la forme différentielle ω est fermée.
Lorsque ω = dα, on dit que la forme différentielle ω est exacte.
Théorie globale
U n lemme de Poincaré global n'existe pas. Par exemple, sur le plan
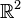
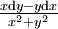
Dans le cas général, le p-ème groupe de cohomologie de de Rham mesure l'obstruction pour une forme fermée à être exacte.
Notations
- Zp(M) l'espace des p-formes fermées.
- Bp(M) le sous-espace des p-formes exactes.
Définition : groupes de cohomologie (de de Rham)
On définit le p-ème groupe de cohomologie de De Rham Hp(M) comme étant l'espace quotient de Zp(M) par Bp(M) :
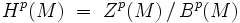
c'est-à-dire l'espace des p-formes fermées modulo le sous-espace des p-formes exactes.
Exemples
-
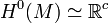
- Si M est une variété lisse compacte connexe et orientable de dimension n, alors Hn(M) est de dimension 1.
- Si M., n'est pas orientable (les autres hypothèses restant les mêmes), Hn(M) = 0
- Hk(Sn) = 0 pour 0 < k < n
Théorie locale (Lemme de Poincaré)
On a pour tout p la relation
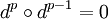
Théorème — Toute forme différentielle exacte est fermée.
Le lemme de Poincaré permet de montrer que la réciproque est vraie localement :
Lemme de Poincaré — Toute forme différentielle fermée est localement exacte.
Plus précisément pour toute forme fermée définie sur un ouvert U de M contenant x, il existe un voisinage de x contenu dans U sur lequel la restriction de la forme est exacte.
En effet si