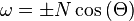Fréquence de Brunt-Väisälä - Définition

Bibliographie

• Holton, James R., An Introduction to Dynamic Meteorology, 4^e édition, Academic Press, New York, décembre , 535 p. , p. 50-53 
• Lighthill, J., Waves in Fluids, Cambridge University Press, 1978 
• Mowbray,D.E. et B.S.H.Rarity, « A theoretical and experimental investigation of the phase configuration of internal waves of small amplitude in a density stratified liquid », dans Journal of Fluid Mechanics, n^o 28, 1967, p. 1-16 
• Rogers, R. R. et Yau, M. K., Short Course in Cloud Physics, 3^e édition, Butterworth-Heinemann, 1^e janvier 1989, 304 p. , p. 30-35.
  EAN 9780750632157
   
• Tritton, D.J., Physical Fluid Dynamics. 2^e édition, Oxford University Press, 1988 

Propriétés

Les ondes de gravité ont plusieurs propriétés qui s'interprètent à partir de leur fréquence, parmi lesquelles on remarque :

• la direction de propagation de ces ondes dépend de la fréquence du forçage et aussi de la fréquence de Brunt-Väisälä locale (stratification de densité locale) ;
• la vitesse de phase (vitesse de propagation des fronts d'onde) et la vitesse de groupe (vitesse avec laquelle l'énergie des ondes est transmise) des ondes internes sont perpendiculaires.

En utilisant l'approximation de Boussinesq, on peut trouver la relation de dispersion des ondes générées par :

où ω est la fréquence d'excitation utilisée, N est la fréquence de Brunt-Väisälä et Θ est l'angle des fronts d'ondes par rapport à la verticale.