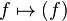Géométrie algébrique - Définition
La liste des auteurs de cet article est disponible ici.
Balbutiements
L'introduction des coordonnées par René Descartes permet de faire un lien entre certains objets géométriques et certaines équations algébriques, ne faisant intervenir que les quatre opérations élémentaires. Cette propriété ne dépend pas du choix du système de coordonnées, car cela revient à effectuer une transformation affine qui ne change pas l'éventuelle nature algébrique des équations satisfaites par les points du-dit objet. C'est par exemple le cas :
- des droites (ax + by + c = 0 dans le plan), des plans et plus généralement des sous-espaces affines d'un espace affine ;
- des coniques : cercles, ellipses, paraboles (y − x2 = 0 par exemple), hyperboles (xy − 1 = 0 par exemple).
Mais, par exemple, ce n'est pas le cas de la sinusoïde (elle rencontre une infinité de fois la droite y = 0 ce qui est impossible : supposons qu'elle soit donnée par une seule équation polynomiale f(x,y) = 0. Comme le polynôme en une variable f(x,0) s'annule une infinité de fois, il est identiquement nul et f s'annule donc sur l'axe y = 0, ce qui n'est pas le cas).
Étant donné un corps algébriquement clos k, on appellera plus généralement sous-variété algébrique affine de kn tout sous ensemble de kn qui soit le lieu d'annulation commun d'un certain nombre de polynômes à n variables et à coefficients dans k. Ce qu'on notera ici
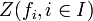
![f_i\in k[\mathrm{X}_1,\dots,\mathrm{X}_n]](https://static.techno-science.net/illustration/Definitions/autres/1/1c3470460a2b462bb03836a96100f906_95e6d9b141ea6f429bc49a830caa5eda.png)
![k[\mathrm{X}_1,\dots,\mathrm{X}_n]](https://static.techno-science.net/illustration/Definitions/autres/3/37d08829fe65dc3cad21ce052e2d4489_cd78489de3a3f57b1db1c5c96caa1d51.png)
Il est courant pour étudier un objet, d'étudier certaines bonnes fonctions partant de cet objet (dual d'un espace vectoriel, caractères d'un groupe...). Il s'agit ici des fonctions dites régulières : elles partent de la variété et atterrissent dans k en s'exprimant polynomialement en les coordonnées. L'ensemble des fonctions régulières est isomorphe à la k-algèbre réduite de type fini
![k[\mathrm{X}_1,\dots,\mathrm{X}_n]/I](https://static.techno-science.net/illustration/Definitions/autres/0/036496e7469d5d16c980c8836afca708_5b5d63902db12d70e997d989a95b10fd.png)
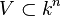
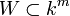
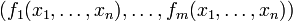
Aspects globaux
A l'instar de ce qu'on fait en géométrie différentielle, on pourrait définir nos objets globaux comme étant des espaces topologiques, mais qui ressemblent localement à une variété affine en imposant en outre des changements de cartes polynomiaux. Ce n'est pas ce point de vue que l'on choisit, mais celui des faisceaux. On appelle alors schéma tout espace annelé en anneau locaux qui admet un recouvrement par des ouverts Ui, qui munit du faisceau induit, sont isomorphes à des spectres d'anneaux Ai. Un morphisme entre schémas n'est rien d'autre qu'un morphisme d'espaces annelés en anneaux locaux.
Pour étudier un tel schéma X, on peut s'intéresser à l'ensemble des bonnes fonctions Γ(X), celles qui sont localement régulières ; ceci souffre de deux défauts :
- Un défaut d'exactitude, ce qui donne lieu à une cohomologie des faisceaux, autrement dit une suite de groupes Hn mesurant le défaut d'exactitude de H0 = Γ(X). Lorsque X est une k-variété, les Hn sont des k-espaces vectoriels de dimension finie et même nuls pour tout indice plus grand que la dimension du schéma ;
- Une trop grande rigidité . On peut alors élargir la classe des bonnes fonctions aux fonctions rationnelles en inversant les fonctions régulières non identiquement nulles. Ce ne sont plus des fonctions à proprement parler car « le dénominateur peut s'annuler ».
Dans le cas d'une courbe lisse irréductible, le corps des fonctions rationnelles s'identifiant aux corps des fractions de l'anneau des fonctions régulières, il contient tous les anneaux de germes qui en sont des localisés. Comme ils sont de plus réguliers et de dimension 1, ils sont de valuation discrète. Une telle valuation s'étend aux fonctions rationnelles et mesure précisément la multiplicité du point : dans le cas positif, c'est un zéro, dans le cas négatif, un pôle et sauf pour un nombre fini de point c'est nul. On étudie alors des espaces de fonctions rationnelles astreintes à avoir des zéros en P de multiplicité au moins nP > 0 et des pôles d'ordre au plus nP < 0. Le théorème de Riemann-Roch relie la dimension d'un tel espace au genre de la courbe.
Plus généralement, on appelle diviseur sur une courbe (cela peut s'étendre en dimension plus grande) toute somme finie de points fermés de la courbe P
| ∑ | nP |
| fini |
. On appelle degré d'un tel diviseur l'entier relatif
| ∑ | nP[k(P):k] |
| fini |
où [k(P):k] désigne « le degré du point » : typiquement, les points réels d'un schéma réel sont de degré 1 et les points complexes de degré 2 (cf.
![x^2+1\in spec \mathcal{R}[x]](https://static.techno-science.net/illustration/Definitions/autres/3/3ade55a06e17003ce584bae77bcf2d86_19699288516b998f620a526492122ab2.png)