Grafcet - Définition

Séquence unique et séquences multiples

1. Séquence unique : un automatisme est décrit par un grafcet à séquence unique lorsqu'il peut être représenté par un ensemble de plusieurs étapes formant une suite dont le déroulement s'effectue toujours dans le même ordre. (Le grafcet ci-dessus en est un exemple)

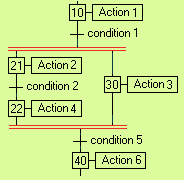
2. Séquences multiples simultanées : lorsque le franchissement d'une transition conduit à activer plusieurs étapes, les séquences issues de ces étapes sont dites « séquences simultanées ». Les séquences simultanées débutent toujours sur une réceptivité unique et se terminent toujours sur une réceptivité unique. En effet, les différentes séquences « démarrent » en même temps puis évoluent ensuite indépendamment les unes des autres. Ce n'est donc que lorsque toutes les étapes finales de ces séquences sont actives simultanément (ce qui se produit souvent après attente réciproque) que l'évolution peut se poursuivre par le franchissement simultané d'une même transition. Le début et la fin des séquences simultanées sont représentés par deux traits parallèles (en rouge, fig. ci-contre), qui ne constituent pas des entités spécifiques du grafcet, mais qui doivent être compris comme l'élargissement de l'entrée ou de la sortie de la transition. (On parle parfois de « divergence » et de « convergence en ET » pour cette représentation.)

3. Séquences multiples exclusives : Lorsque, à partir d'une étape, on peut effectuer un choix entre plusieurs séquences possibles conditionnées par plusieurs réceptivités exclusives, c'est une « sélection de séquences » ou « aiguillage ». Pour une meilleure lisibilité, les différentes séquences possibles sont installées sous un trait horizontal (en rouge fig. ci-contre) qui représente l'élargissement de la sortie de l'étape, et se retrouvent par un trait analogue représentant l'entrée de l'étape à nouveau commune. D'une façon analogue au double trait vu ci-dessus, on parle de « divergence » et de « convergence en OU » pour cette représentation.

Deux cas particuliers de sélection de séquences se rencontrent fréquemment dans la plupart des automatismes séquentiels. Ce sont le saut d'étape et la reprise de séquence :

1. Le saut d'étapes permet de sauter un certain nombre d'étapes si une condition logique est réalisée (c'est le cas général, avec une branche vide d'action).
2. La reprise de séquence permet de répéter une même séquence jusqu'à ce que la réceptivité de fin de séquence soit vraie.

Si les réceptivités ne sont pas exclusives (par exemple, si c12 et c13 peuvent être vraies au même moment), la suite est indéterminée ; le grafcet est fautif ou pas.

Nature des réceptivités

Il s'agit toujours du résultat d'une expression booléenne unique pouvant faire intervenir

1. Des états de variables booléennes (état direct, front, fin de temporisation...)
2. Des comparaisons sur des valeurs numériques.
3. Des tests sur les états actifs d'étapes (permis mais à éviter pour une meilleure lisibilité).
4. etc.

Nature des actions

Le critère de classification des actions les plus utilisées est : la durée de l'action comparativement à la durée de l'étape :

• Action continue : l'action se poursuit tant que l'étape à laquelle elle est associée est active. Cela se traduit par le diagramme temporel (chronogramme 1) ci-contre.
• Action conditionnelle : l'action est exécutée si, en plus de l'activité de l'étape à laquelle elle est associée, une condition logique spécifiée est vraie (voir chronogramme 2 ci-contre). Ces actions conditionnelles sont particulièrement importantes car elles permettent, dans une étape, de réaliser une combinatoire locale en vue, par exemple, d'exécuter l'action seulement pendant un certain temps, ou après un certain temps d'activité de l'étape (voir les chronogrammes 3 et 4 ci-contre).
• Action : pour maintenir la continuité d'une action devant se prolonger pendant l'activité de plusieurs étapes, il est possible :
  • de répéter l'action continue dans toutes les étapes concernées ;
  • de mémoriser l'action par des fonctions mises à 1 (SET) et mises à zéro (RESET).

La figure ci-dessous présente ces différentes méthodes équivalentes de maintien d'une action sur plusieurs étapes :