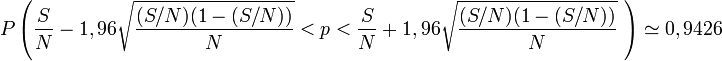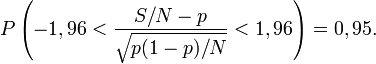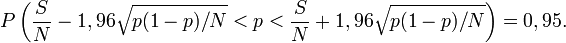Intervalle de confiance - Définition
La liste des auteurs de cet article est disponible ici.
Exemple II : le sondage d'opinion
On cherche à estimer le pourcentage de personnes ayant une voiture verte. Pour cela on effectue un sondage. Comme on ne sonde pas toute la population on a de bonnes chances de ne pas tomber exactement sur la bonne valeur mais de faire une erreur. On veut alors donner un intervalle qui a 95% de chances de contenir la vraie valeur.
Pour cela on effectue un sondage sur 1 000 personnes. Les résultats sont les suivants: 150 personnes ont une voiture verte, 850 n'en ont pas.
On appelle p la « vraie » proportion de personnes dans la population totale qui ont une voiture verte. On cherche à estimer p. On appelle N le nombre de personnes ayant été sondées, ici N = 1000. On appelle S le nombre de personnes ayant une voiture verte parmi les N personnes sondées. L’idée est de présenter comme estimation de p la valeur
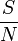
On applique le théorème central limite à la variable aléatoire Xi qui vaut 1 si la i-ème personne sondée a une voiture verte et 0 sinon. Cette variable a une moyenne p et une variance p(1 − p). Alors:
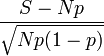
Pour une loi normale de moyenne 0 et de variance 1 on a : P(−1,96 < Z < 1,96) = 0,95. La valeur 1,96 est le quantile d'ordre 1-2,5% de la loi normale. Ces valeurs peuvent se trouver dans des tables de quantiles ou être calculées à partir de la fonction d'erreur réciproque:
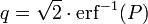
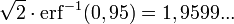
Soit encore
En estimant
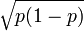
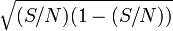
En fait si on appelle
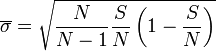
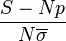
-
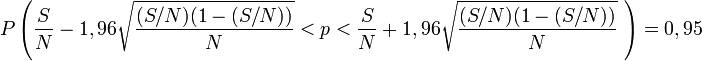
L'intervalle de confiance à 95 % vaut alors [0,127;0,172]. On est sûr à 95% qu'entre 12,7% et 17,2% de personnes ont une voiture verte avec ce sondage.
Pour avoir une plus grande précision, il faudrait sonder plus de personnes. On remarque en effet l'existence d'un N apparaissant au dénominateur des deux racines carrées. Si on sonde plus de personnes (N plus grand), ces deux termes auront tendance à devenir plus petits et l'intervalle sera plus petit.
Remarque. Suite aux diverses approximations du raisonnement, le résultat d'une confiance à 95% n'est pas toujours assuré. On arrive à un résultat inférieur à 95% pour certaines valeurs de p et N, par exemple
- si N = 100 et p = 0,5, alors
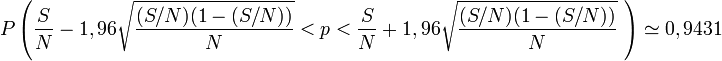
- si N = 100 et p = 0,37, alors
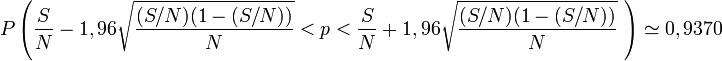
- si N = 150 et p = 0,4245, alors