Lemme de Schur - Définition
La liste des auteurs de cet article est disponible ici.
Cas des groupes finis
Corollaire 3
-
- Soient (E, ρ1) et (F, ρ2) deux représentations de G irréductibles sur un corps K de caractéristique soit nulle soit première avec g l'ordre du groupe et contenant le corps de décomposition du polynôme Xg - 1 et ψ une application linéaire de E dans F, on définit l'application linéaire φ de E dans F par :
-
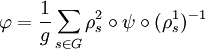
- (1) Si les représentations ne sont pas isomorphes, φ est nulle.
- (2) Si le corps K est de caractéristique nulle et algébriquement clos et si E est égal à F, alors φ est une homothétie de rapport 1/n.Tr(ψ), où n désigne de degré des représentations.
- Vérifions dans un premier temps que φ vérifie la propriété suivante :
Remarquons tout d'abord que l'application de G dans G qui à s associe ts est une permutation de G, si t est un élément de G. On en déduit que :
- (1) Comme les représentations ne sont pas isomorphes φ ne peut être à la fois injective et surjective. Le lemme de Schur montre que, comme φ n'est pas un automorphisme, φ est l'application nulle.
- (2) Si E est égal à F, les hypothèses du corollaire 1 sont vérifiées ce qui montre que φ est une homothétie. Dans ce cas, les deux représentations sont identiques et l'expression définissant φ est la moyenne de g applications toutes semblables à ψ et donc ayant la même trace que ψ. Les traces de φ et ψ sont donc égales. Comme pour toute homothétie, φ est de rapport 1/n.Tr(φ), comme les traces de φ et de ψ sont égales, nous avons démontré que le rapport de l'homothétie est égal à 1/n.Tr(φ).
Corolaire 4
C'est un quatrième corolaire qui est utilisé dans la théorie des caractères. Elle correspond à la traduction en termes de matrice du corolaire précédent. Utilisons les notations suivantes, soit A et B deux représentations sous forme matricielle d'un groupe fini G d'ordre g sur un même corps K de caractéristique soit nulle soit première avec la dimension de A et g et tel que le polynôme Xg - 1 soit scindé. Les dimensions respectives de E et F sont notées n et m. L'image d'un élément s de G par A (resp. B) est noté aij(s) (respbij(s))
On a alors le corolaire suivant avec les hypothèses du corolaire précédent :
-
- (1) Si les représentations R1 et R2 ne sont pas isomorphes, alors :
- (2) Si les deux représentations sont isomorphes, alors :
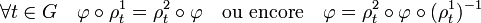
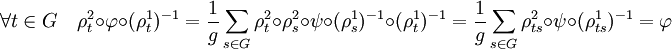
![\forall i,j \in [1,n] \; \forall k,l \in [1,m] \quad \sum_{s\in G} a_{ij}(s).b_{kl}(s^{-1})=0](https://static.techno-science.net/illustrationWebp/Definitions/autres/8/845f3fba1e203334196fd4c2271b4aa8_8e46b2e567704599f6f75ad397fa572c.png)
![\forall i,j,k,l \in [1,n] \quad \frac{1}{g}\sum_{s\in G} a_{ij}(s).b_{kl} (s^{-1})=\frac{1}{n}\delta_{il}\delta_{jk}](https://static.techno-science.net/illustrationWebp/Definitions/autres/6/66e00978d20f713f0e473c1bd04ea4fb_efb92cdebe070fcec4114b823a1e56d3.png)
Où δij désigne le symbole de Kronecker.
- Montrons la proposition (1) :
Si C une matrice de dimension mxn de coefficients (cjk), la traduction du point (1) du corollaire précédent montre que :
![\sum_{s\in G} A_s.C.B_{s^{-1}} = 0 \quad donc \quad \forall i\in [1,n] \; \forall l\in [1,m] \quad \sum_{jk} \sum_{s\in G} a_{ij}(s).c_{jk}.b_{kl}(s^{-1})= \sum_{jk} \left(\sum_{s\in G} a_{ij}(s).b_{kl}(s^{-1})\right).c_{jk}=0](https://static.techno-science.net/illustrationWebp/Definitions/autres/9/9330ef33525210dbf56f82ea8271f80b_8ae6baac004f71a945b7795cd5ff354a.png)
Cette égalité est vraie pour toute matrice C, donc pour toute valeur de cjk, ce qui démontre la proposition (1).
- Montrons la proposition (2) :
Avec les mêmes notations (maintenant m est égal à n), on obtient d'après le point (2) du corollaire précédent :
![\frac{1}{g}\sum_{s\in G} A_s.C.B_{s^{-1}} = \frac{1}{n}Tr(C).Id \quad donc \quad \forall i,j\in [1,n] \quad \frac{1}{g}\sum_{jk} \sum_{s\in G} a_{ij}(s) .c_{jk} .b_{kl}(s^{-1})= \frac{1}{n}\sum_k c_{kk}.\delta_{il}](https://static.techno-science.net/illustrationWebp/Definitions/autres/2/2e1b6ce8f99be35630ccd400658c205c_d5fae0d53b73c1249278a5bacddad6fa.png)
On en déduit :
Et la proposition (2) est démontrée.
