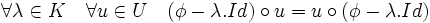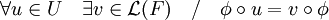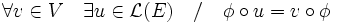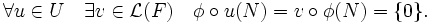Lemme de Schur - Définition

Corollaires

Corollaire 1

• Soient E un espace vectoriel de dimension finie sur un corps K algébriquement clos et U une partie irréductible de L(E). Si un endomorphisme Φ de E commute avec tout élément de U, alors Φ est une homothétie.

En effet,on peut écrire, si Id désigne l'application identité :

On en déduit par application du lemme de Schur que Φ - λ.Id est un automorphisme ou est nulle. Soit λ^* une valeur propre de Φ, alors Φ - λ^*.Id est l'application nulle, ce qui démontre le corollaire.

Dans le cas de la représentation d'un groupe fini d'ordre g, alors tout automorphisme de l'image possède pour polynôme annulateur P[X] = X^g - 1. En conséquence, si K contient le corps de décomposition de P[X] le corollaire s'applique encore.

Corollaire 2

• Toute représentation irréductible dans un espace de dimension finie d'un groupe abélien G sur un corps algébriquement clos est de dimension 1.

En effet, soit ρ le morphisme de la représentation. Quel que soit l'élément s de G ρ_s commute avec tous les endomorphismes de la représentation. D'après le corolaire 1 ρ_s est une homothétie. Si la dimension de l'espace de représentation était strictement supérieure à 1, chaque sous-espace de dimension 1 étant ainsi invariant on aboutirait à une contradiction.

Lemme

Énoncé

Soient E et F deux K espaces vectoriels et Φ une application linéaire non nulle de E dans F.

• (1) S'il existe une partie irréductible U de L(E) telle que :

Alors Φ est injective.

• (2) S'il existe une partie irréductible V de L(F) telle que :

Alors est surjective.

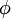
Démonstration

(1) Si Φ n'est pas injective, son noyau N est non nul (et non égal à E puisque Φ est non nulle). On a alors :

Il en résulte que u(N) est inclus dans N, ce qui est contradictoire avec l'hypothèse d'irréductibilité de U.
(2) Les propriétés suivantes sont vérifiées :

.

L'image de Φ est donc stable par tous les éléments de V. Il en résulte par irréductibilité de V (et le fait que Φ est non nulle) que l'image de Φ est égale à F.

Applications

Caractère

C'est la première application historique du lemme. Soient G un groupe fini d'ordre g, (E, ρ¹) et (F, ρ²) deux représentations de G irréductibles. On suppose ici que le corps K est celui des nombres complexes. On note χ₁ et χ₂ les caractères des deux représentations. Les caractères sont éléments de l'espace vectoriel noté C des applications de G dans le corps de complexes de dimension. Sa dimension est égale à g. On munit C du produit hermitien < | > suivant :

Si y désigne un nombre complexe, y^* désigne ici son conjugué.

• Les caractères irréductibles d'un groupe fini, si le corps possède forment famille orthonormale de C.

En effet, c'est une conséquence directe du corollaire 4. L'article associé démontre que la trace de l'inverse de s est égale au conjugué de la trace de s, si s est un élément de G. En utilisant les notations du paragraphe précédent, on obtient :

Si les deux représentations ne sont pas isomorphes, alors la proposition (1) du corollaire permet de conclure à l'orthogonalité. Si les deux représentations sont isomorphes,d'après la proposition (2) on obtient :

Ce qui démontre la proposition. Ce résultat est un des fondements de la théorie des caractères.
La remarque sur la clôture algébrique au début du paragraphe sur les groupes finis permet d'étendre ce résultat à tout les corps commutatifs de caractéristique nulle.

Groupe abélien fini

D'autres applications existent. Le lemme de Schur permet de démonter directement que tout groupe abélien fini est un produit de cycles. La démonstration se fonde essentiellement sur l'algèbre linéaire et est donnée dans l'article Diagonalisation.

Ce résultat se démontre aussi directement (cf article détaillé), ou par l'analyse des caractères.