Lentille optique - Définition
La liste des auteurs de cet article est disponible ici.
Caractéristiques d’une lentille
On considère ici que l’on est dans les conditions de Gauss, et que le système est stigmatique : tous les rayons issus d’un point A convergent — après traversée de la lentille — en un point A′, ou semblent provenir d'un point A′ situé en amont de la lentille. A est appelé point objet, et A′ est le point image de A.
Un système optique est un ensemble de milieux transparents et homogènes ou réflecteurs, séparés par des dioptres. Un système optique centré possède une symétrie de révolution autour d’un axe appelé axe optique. Une lentille seule possède donc un tel axe. On appelle centre optique le point de cet axe situé au milieu de la lentille.
Foyers objet et image
- On appelle foyer image F′ l’image d’un objet situé à l’infini : c’est donc le point où focalisent des rayons qui se propagent parallèlement à l’axe optique.
- On appelle foyer objet F le point dont l’image est située à l’infini : les rayons issus de ce point se propagent — après traversée de la lentille — parallèlement à l’axe optique.
Le plan perpendiculaire à l’axe optique et passant par F′ est appelé plan focal image, et ses points sont des foyers image secondaires.
Distances focales
En optique, on utilise des distances algébriques, marquées par une barre au-dessus de la quantité considérée, le sens de propagation de la lumière étant par convention le sens positif. On discerne deux distances focales :
- ƒ′ = SF′
et
- ƒ = SF,
où S est le centre optique de la lentille.
La distance algébrique ƒ′ est positive si F′ est situé en aval de la lentille (lentille convergente) et négative si F′ est en amont de la lentille (lentille divergente).
La détermination expérimentale de la distance focale ƒ′ d'une lentille optique s’appelle la focométrie.
Espaces objet et image
On considère une onde lumineuse se propageant selon un sens donné. Le demi-espace situé en amont de la lentille par rapport à ce sens de propagation est appelé espace objet. Le demi-espace situé en aval de la lentille est appelé espace image.
Si A est un objet situé en aval de la lentille, A est un objet virtuel et S2A est positif ; si A est un objet réel situé en amont de la lentille, cette distance est négative. Pour une image réelle A′ située en aval de la lentille, S1A′ est positif, et pour une image virtuelle située en amont de la lentille, S1A′ est négatif (pour une lentille divergente, en prenant les notations des images ci-dessus, il faut inverser S1 et S2).
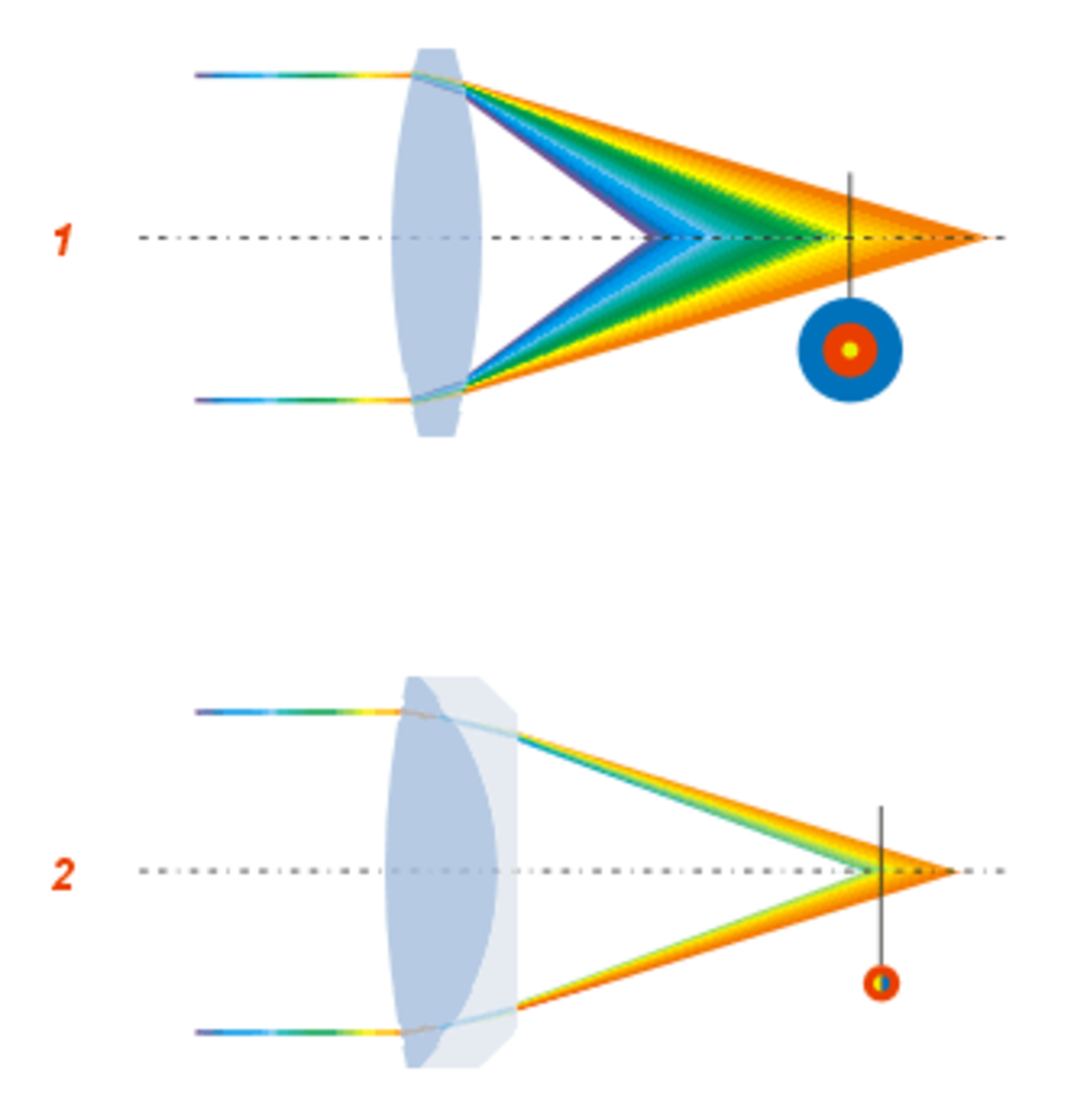
Aberrations
Les lentilles optiques ne forment pas des images parfaites : l’image d’un point n’est généralement pas un point, mais une tache (astigmatisme). Ces aberrations affectent la qualité des images, mais peuvent cependant être minimisées par l’association de deux lentilles de verres optiques différents qui agissent en correction.
On classe les aberrations en 2 grandes familles :
- aberrations chromatiques : l’image se forme différemment selon la couleur de la lumière.
- aberrations géométriques, qui caractérisent les écarts à l’optique géométrique, écarts d’autant plus grands que l’on s’éloigne des conditions de Gauss, donc de l’axe optique.