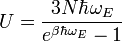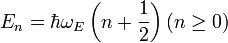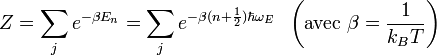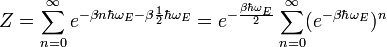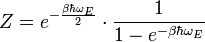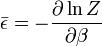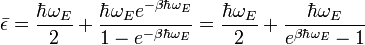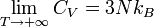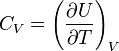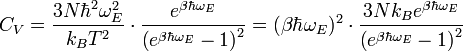Modèle d'Einstein - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En physique statistique et en physique du solide, le modèle d’Einstein est un modèle permettant de décrire la contribution des vibrations du réseau à la capacité calorifique d’un solide cristallin. Il est basé sur les hypothèses suivantes :
- chaque atome de la structure est un oscillateur harmonique quantique 3D,
- les atomes vibrent à la même fréquence, contrairement au modèle de Debye.
Ce modèle est nommé d’après Albert Einstein, qui l'a proposé en 1907.
Énergie interne
Les vibrations du réseau cristallin sont quantifiées, c’est-à-dire que les énergies de chaque mode normal de vibration ne peuvent prendre que des valeurs discrètes
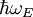
L’énergie interne U du solide est donnée par la formule :
où ℏ est la constante de Planck réduite, ω est la pulsation d’un oscillateur, N le nombre d’atomes qui constituent le système et
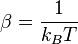
L’énergie d’un oscillateur harmonique à une dimension vibrant à la fréquence
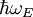
où n est un nombre quantique
On calcule la fonction de partition d’un oscillateur harmonique quantique qui est donnée par la relation :
où kB est la constante de Boltzmann, T la température absolue et j est un état de l’oscillateur. Il y a un seul état par niveau d’énergie ; la somme devient donc :
En appliquant la formule de la somme d’une suite géométrique, on simplifie la fonction de partition :
On obtient alors l’énergie d’un oscillateur :
avec
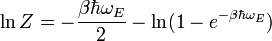
On remarque au passage que
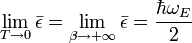
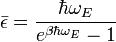
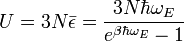
Résultats du modèle
Le modèle d’Einstein retrouve la loi de Dulong et Petit, pour les hautes températures :
Cependant, à basse température, ce modèle concorde moins avec les mesures expérimentales que celui de Debye :
Lorsque
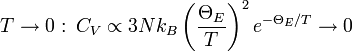
Cette discordance avec l’expérience peut s’expliquer en abandonnant l’hypothèse selon laquelle les oscillateurs harmoniques vibrent à la même fréquence.
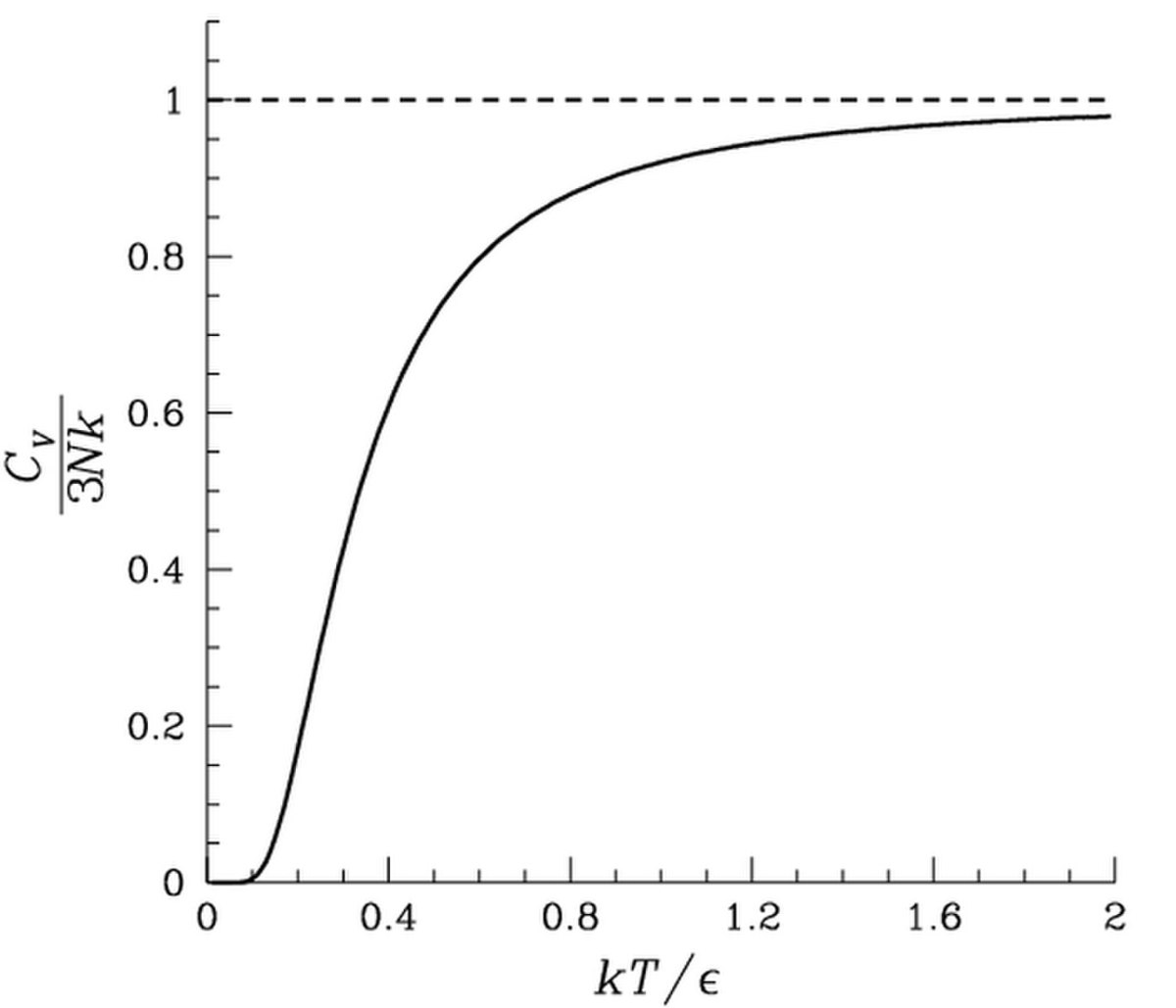
Capacité calorifique
La capacité calorifique CV est définie par :
avec
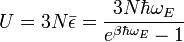
On peut définir la température d’Einstein comme
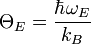
![C_V\left(T\right) = 3Nk_B\cdot\left(\frac{\Theta_E}{T}\right)^2\cdot\frac{\exp\left(\frac{\Theta_E}{T}\right)}{\left[\exp\left(\frac{\Theta_E}{T}\right)-1\right]^2}](https://static.techno-science.net/illustration/Definitions/autres/c/c49cda319d9278b01ec813164c1e3142_699bc8af6605af60dc67d9b53ff7bd2f.png)