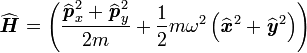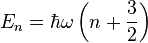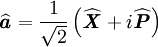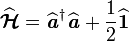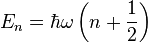Oscillateur harmonique quantique - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - L'oscillateur harmonique classique à une dimension - Généralisation à trois dimensions - L'oscillateur harmonique quantique à une dimension - Oscillateur anharmonique

Introduction

Un oscillateur est un système périodique dans le temps. L'harmonicité indique que l'on considère le potentiel associé comme une parabole. Cette approximation est justifiée dans la plupart des cas, à condition que l'amplitude de l'oscillation ne soit pas trop élevée. C'est pour cela que le concept d'oscillateur harmonique joue un rôle majeur dans de nombreuses applications de la physique.
La mécanique quantique a révolutionné un grand nombre de concepts fondamentaux. L'oscillateur harmonique a aussi subi une reformulation dans ce cadre quantique, ce qui a permis d'élucider plusieurs résultats expérimentaux, notamment en physique de la matière condensée.

L'oscillateur harmonique classique à une dimension

Un oscillateur harmonique classique à une dimension est modélisé par un potentiel parabolique, typiquement :

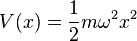
$V(x) = \frac{1}{2}m\omega^2 x^2$

On prouve alors facilement qu'une particule de masse $m$ dans ce potentiel a un mouvement sinusoïdal de pulsation $ω$ .

Généralisation à trois dimensions

Ces calculs pour une seule dimension se généralisent très bien à 3 dimensions. L'hamiltonien est alors simplement sous la forme d'une somme de trois hamiltoniens indépendants, qui sont donc étudiables séparement exactement comme nous l'avons fait précédemment.

Les énergies accessibles par l'oscillateur sont :

avec $n = n x + n y + n z$ : l'énergie dépend de trois nombres quantiques indépendants. Pour une même énergie, il va donc être possible d'imaginer des configurations différentes : les niveaux d'énergie sont dégénérés.

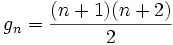
On calcule le nombre de dégénérescences pour le n-ième niveau d'énergie : $g_{n} = \frac{(n+1)(n+2)}{2}$

L'oscillateur harmonique quantique à une dimension

Position du problème

Pour faire une étude quantique de ce type d'oscillateurs, il faut écrire l'opérateur hamiltonien correspondant :

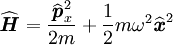
$\widehat{\textbf{\textit{H}}}=\frac{\widehat{\textbf{\textit{p}}}_{x}^2}{2m} + \frac{1}{2}m \omega^2 \widehat{\textbf{\textit{x}}}^2$

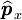
où $\widehat{\textbf{\textit{p}}}_{x}$ est la composante sur l'axe $x$ de l'opérateur impulsion de la particule.

Il faut alors résoudre l'équation de Schrödinger indépendante du temps associée à cet hamiltonien :

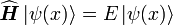
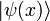
$\widehat{\textbf{\textit{H}}}\left | \psi (x) \right \rangle = E\left | \psi (x) \right \rangle$ où $E$ est l'énergie associée à une fonction d'onde $\left | \psi (x) \right \rangle$ .

On peut déjà formuler quelques remarques :

Comme V est positif ou nul, alors les valeurs propres $E$ seront positives ou nulles.
Le confinement de la particule dans ce potentiel indique que le spectre de ces énergies sera discret.
Le système ne fait apparaître qu'un seul degré de liberté, il y aura donc un seul nombre quantique.

Simplification de l'hamiltonien

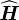
Pour simplifier l'écriture de $\widehat{\textbf{\textit{H}}}$ , on pose les opérateurs suivants :

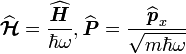
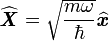
$\widehat{\boldsymbol{\mathcal{H}}}=\frac{\widehat{\textbf{\textit{H}}}}{\hbar\omega}, \widehat{\textbf{\textit{P}}}=\frac{\widehat{\textbf{\textit{p}}}_{x}}{\sqrt{m\hbar\omega}}$ , et $\widehat{\textbf{\textit{X}}}=\sqrt{\frac{m\omega}{\hbar}} \widehat{\textbf{\textit{x}}}$

( $\hbar$ est la constante de Planck réduite).

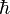
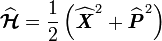
Cela nous permet de réécrire l'hamiltonien sous la forme simple : $\widehat{\boldsymbol{\mathcal{H}}}=\frac{1}{2}\left(\widehat{\textbf{\textit{X}}}^2+\widehat{\textbf{\textit{P}}}^2 \right)$ .

On définit alors un nouvel opérateur :

Remarques :

$\left[ \widehat{\textbf{\textit{X}}},\widehat{\textbf{\textit{P}}} \right] = \frac{1}{\hbar}\left[ \widehat{\textbf{\textit{x}}} , \widehat{\textbf{\textit{p}}}_{x} \right] = i\widehat{\textbf{1}}$
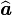
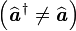
$\widehat{\textbf{\textit{a}}}$ n'est pas un opérateur hermitien $\left( \widehat{\textbf{\textit{a}}}^{\dagger} \ne \widehat{\textbf{\textit{a}}} \right)$ .
Cependant, on a le commutateur : $\left[ \widehat{\textbf{\textit{a}}},\widehat{\textbf{\textit{a}}}^{\dagger} \right]=\widehat{\textbf{1}}$ .
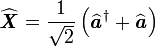
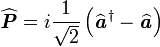
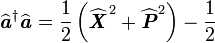
On démontre facilement : $\widehat{\textbf{\textit{X}}}=\frac{1}{\sqrt{2}}\left(\widehat{\textbf{\textit{a}}}^\dagger+\widehat{\textbf{\textit{a}}} \right)$ , $\widehat{\textbf{\textit{P}}}=i\frac{1}{\sqrt{2}}\left(\widehat{\textbf{\textit{a}}}^{\dagger}-\widehat{\textbf{\textit{a}}}\right)$ et $\widehat{\textbf{\textit{a}}}^{\dagger} \widehat{\textbf{\textit{a}}}= \frac{1}{2}\left(\widehat{\textbf{\textit{X}}}^2+\widehat{\textbf{\textit{P}}}^2\right) -\frac{1}{2}$ .

Cela donne finalement l'écriture simplifiée de l'hamiltonien :

Calcul des valeurs propres

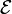
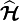
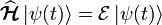
Les valeurs propres $\mathcal{E}$ de l'hamiltonien $\widehat{\boldsymbol{\mathcal{H}}}$ vérifient, par définition, l'équation : $\widehat{\boldsymbol{\mathcal{H}}}\left | \psi (t) \right \rangle = \mathcal{E}\left | \psi (t) \right \rangle$ .
On développe plusieurs points :

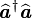
Les valeurs propres $n$ de l'opérateur $\widehat{\textbf{\textit{a}}}^\dagger \widehat{\textbf{\textit{a}}}$ sont positives ou nulles.
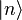
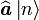
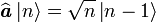
Si $n$ est une valeur propre associée au vecteur propre $\left | n \right \rangle$ , alors $n - 1$ est aussi valeur propre associée au vecteur $\widehat{\textbf{\textit{a}}} \left | n \right \rangle$ . Cela donne alors $\widehat{\textbf{\textit{a}}} \left | n \right \rangle=\sqrt{n}\left | n-1 \right \rangle$ .
De même, $\widehat{\textbf{\textit{a}}}^\dagger\left | n \right \rangle=\sqrt{n+1}\left | n+1 \right \rangle$ .
$n$ doit être entier.

Les résultats précédents donnent alors :

Les énergies accessibles par l'oscillateur sont :

Ainsi, les énergies accessibles par l'oscillateur sont quantifiées. Ce résultat a de nombreuses répercussions en physique statistique par exemple.

Calcul des états propres

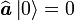
On vérifie que pour l'état fondamental on a l'équation suivante : $\widehat{\textbf{\textit{a}}} \left | 0 \right \rangle = 0$
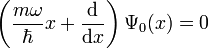
On repasse par la définition de $a$ pour trouver $\left(\frac{m \omega}{\hbar} x + \frac{\mathrm{d}}{\mathrm{d}x}\right)\Psi_{0}(x) = 0$
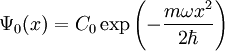
On résout cette équation différentielle : $\Psi_{0}(x) = C_{0} \exp\left(- \frac{m \omega x^{2}}{2 \hbar}\right)$
En normalisant ce résultat, on trouve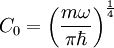 $C_{0} = \left(\frac{m \omega}{\pi \hbar}\right)^{\frac{1}{4}}$
Les solutions étant proportionnelles entre elles, on en déduit que cet état fondamental est non dégénéré.
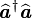
Une démonstration par récurrence montre que les états propres de $\widehat{\textbf{\textit{a}}}^\dagger \widehat{\textbf{\textit{a}}}$ s'écrivent : $|n>=\frac{1}{\sqrt{n!}}\left(\widehat{\textbf{\textit{a}}}^\dagger \right)^n |0>$ .
Ce qui nous donne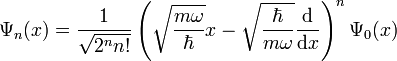 $\Psi_{n}(x) = \frac{1}{\sqrt{2^{n} n!}} \left( \sqrt{\frac{m \omega}{\hbar}} x - \sqrt{\frac{\hbar}{m \omega}}\frac{\mathrm{d}}{\mathrm{d}x} \right) ^{n} \Psi_{0}(x)$

Cette dernière équation nous permet de retrouver explicitement autant de fonctions d'ondes que l'on désire. Par exemple pour $n=1\,$ on obtient :
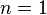
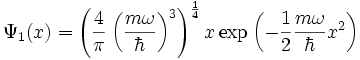
$\Psi_{1}(x) = \left( \frac{4}{\pi} \left( \frac{m \omega}{\hbar} \right )^{3} \right )^{\frac{1}{4}} x \exp \left( -\frac{1}{2} \frac{m \omega}{\hbar} x^{2} \right)$

Représentation matricielle

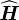
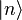
La matrice représentative de l'hamiltonien $\widehat{\textbf{\textit{H}}}$ sur la base des $\vert n \rangle$ est, par construction, diagonale.

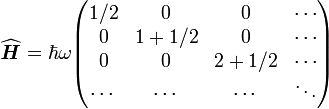
On a $\widehat{\textbf{\textit{H}}}= \hbar \omega \begin{pmatrix} 1/2 & 0 & 0 &\cdots \\ 0 & 1+1/2 & 0 &\cdots \\ 0 & 0 & 2+1/2 &\cdots \\ \cdots & \cdots & \cdots &\ddots \end{pmatrix}$

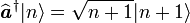
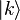
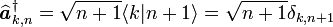
Sachant que $\widehat{\textbf{\textit{a}}}^{\dagger} \vert n \rangle = \sqrt{n+1} \vert n+1 \rangle$ , en multipliant à gauche par $\vert k \rangle$ il vient $\widehat{\textbf{\textit{a}}}^{\dagger}_{k,n}=\sqrt{n+1} \langle k \vert n+1 \rangle = \sqrt{n+1} \delta_{k,n+1}$

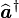
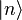
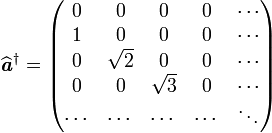
La matrice représentative de $\widehat{\textbf{\textit{a}}}^{\dagger}$ sur la base des $\vert n \rangle$ est donc $\widehat{\textbf{\textit{a}}}^{\dagger}= \begin{pmatrix} 0 & 0 & 0 & 0 & \cdots \\ 1 & 0 & 0 & 0 & \cdots \\ 0 & \sqrt{2} & 0 & 0 &\cdots \\ 0 & 0 & \sqrt{3} & 0 & \cdots \\ \cdots & \cdots & \cdots & \cdots &\ddots \end{pmatrix}$

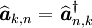
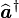
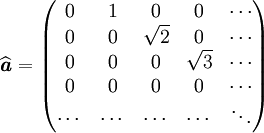
Puisque $\widehat{\textbf{\textit{a}}}_{k,n}=\widehat{\textbf{\textit{a}}}^{\dagger}_{n,k}$ , la matrice $\widehat{\textbf{\textit{a}}}$ est construite en transposant $\widehat{\textbf{\textit{a}}}^{\dagger}$ : $\widehat{\textbf{\textit{a}}}= \begin{pmatrix} 0 & 1 & 0 & 0 & \cdots \\ 0 & 0 & \sqrt{2} & 0 & \cdots \\ 0 & 0 & 0 & \sqrt{3} &\cdots \\ 0 & 0 & 0 & 0 & \cdots \\ \cdots & \cdots & \cdots & \cdots &\ddots \end{pmatrix}$

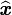
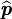
Il est alors facile de construire les matrices représentatives des observables $\widehat{\textbf{\textit{x}}}$ et $\widehat{\textbf{\textit{p}}}$ puisque :

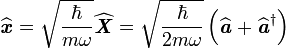
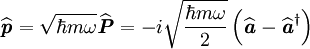
$\widehat{\textbf{\textit{x}}}=\sqrt{\dfrac{\hbar}{m\omega}} \widehat{\textbf{\textit{X}}}= \sqrt{\dfrac{\hbar}{2m\omega}} \left(\widehat{\textbf{\textit{a}}} + \widehat{\textbf{\textit{a}}}^{\dagger}\right)$ et $\widehat{\textbf{\textit{p}}}=\sqrt{\hbar m\omega}\widehat{\textbf{\textit{P}}}=-i\sqrt{\dfrac{\hbar m\omega}{2}}\left(\widehat{\textbf{\textit{a}}} - \widehat{\textbf{\textit{a}}}^{\dagger}\right)$

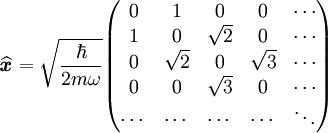
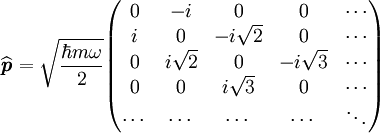
donc $\widehat{\textbf{\textit{x}}}= \sqrt{\dfrac{\hbar}{2m\omega}} \begin{pmatrix} 0 & 1 & 0 & 0 & \cdots \\ 1 & 0 & \sqrt{2} & 0 & \cdots \\ 0 & \sqrt{2} & 0 & \sqrt{3} &\cdots \\ 0 & 0 & \sqrt{3} & 0 & \cdots \\ \cdots & \cdots & \cdots & \cdots &\ddots \end{pmatrix}$ et $\widehat{\textbf{\textit{p}}}= \sqrt{\dfrac{\hbar m\omega}{2}} \begin{pmatrix} 0 & -i & 0 & 0 & \cdots \\ i & 0 & -i\sqrt{2} & 0 & \cdots \\ 0 & i\sqrt{2} & 0 & -i\sqrt{3} &\cdots \\ 0 & 0 & i\sqrt{3} & 0 & \cdots \\ \cdots & \cdots & \cdots & \cdots &\ddots \end{pmatrix}$

Interprétation

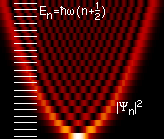
Densité de probabilité |ψ_n(x)|² pour les premières valeurs de l'énergie, en commençant par le fondamental (n = 0) en bas puis en augmentant la valeur de l'énergie en montant. L'axe horizontal correspond à la coordonnée x, les couleurs plus claires indiquent une densité de probabilité plus forte.

En analysant ces fonctions d'ondes, on retrouve de nombreux résultats classiques : la particule dans le puits de potentiel a une probabilité de présence plus élargie si elle a une énergie plus haute (une bille au fond d'un puits va monter plus haut sur les bords si elle a plus d'énergie), la particule a plus de chance de se retrouver sur ces positions éloignées du centre du puits (la bille a une vitesse d'autant plus petite qu'elle est haut dans le puits : elle va donc passer beaucoup plus de temps en hauteur qu'au fond du puits).

États cohérents

D'autres états présentent un intérêt physique. Voir à État cohérent.

Applications

Pour tous les calculs où des particules sont dans un puits de potentiel, l'approximation harmonique est très intéressante (en effet, on remarque que le développement limité à l'ordre 2 d'un puits nous donne une parabole). Par exemple si l'on souhaite étudier un "piège harmonique" à deux dimensions (condensation de Bose-Einstein à 2D) on pourra poser le hamiltonien suivant pour débuter l'étude: $\widehat{\textbf{\textit{H}}} = \left( \frac{\widehat{\textbf{\textit{p}}}_{x}^2+\widehat{\textbf{\textit{p}}}_{y}^2}{2m} + {1\over 2} m \omega^2 \left(\widehat{\textbf{\textit{x}}}^2+\widehat{\textbf{\textit{y}}}^2 \right) \right)$

Oscillateur anharmonique

- Introduction - L'oscillateur harmonique classique à une dimension - Généralisation à trois dimensions - L'oscillateur harmonique quantique à une dimension - Oscillateur anharmonique

Découverte d'une forme de vie étrange sous la glace de l'Antarctique ❄️

Comment les récepteurs olfactifs discriminent-ils les odeurs ? 🌸

Cette batterie au carbone-14 possède une autonomie de plusieurs milliers d'années ! 🔋

Climat: bientôt des températures critiques en Afrique du Nord et au Moyen-Orient 🔥

Des particules de lumière "filmés" dans leur déplacement 🎬

Montre moi tes mains, je te dirai quel buveur d'alcool tu es 🍺

Ces papillons interprètent les "cris" des plantes pour choisir où pondre 🦋

Le nombre d'articles scientifiques rétractés est en hausse ❌

Une nouvelle manière de lire les mémoires magnétiques 🧲

Vous êtes né avant 1986 ? Voici pourquoi vous risquez de développer des troubles psychiques ⚠️

Ce nouveau modèle relie matière noire et inflation cosmique 🌀

Ils ont rendu ce bois bioluminescent: vers un nouveau mode d'éclairage ? 💡

Des mouches dans la station spatiale chinoise Tiangong 🛰️

Cette main-robot nanométrique est capable de saisir des virus (exemple avec la COVID-19) 🖐️

Une étoile dévorée à pleine vitesse par... un trou noir ? 🌟

Cette astuce simple réduit la consommation d'alcool... des femmes 🍷

Découverte: la lumière transforme un isolant en métal 💡

Cet aliment à bannir nourrit les cancers 🍽️

Cette tablette de 3000 ans dévoile une écriture jusqu'alors inconnue ✍️

Découverte d'une chimie des océans refroidissant le climat 🌊

Le télescope James Webb, poussé à ses limites, découvre ces structures incroyablement anciennes 🔭

Le rôle surprenant de la grossesse contre la grippe A 🦠

Découverte d'une nouvelle espèce éteinte grâce à... un accélérateur de particules ⚛️

Une avancée prometteuse pour le déploiement des batteries sodium-ion 🔋

Voici comment et pourquoi le risque de cancer augmente... puis diminue avec l'âge 🧬

Le Soleil bientôt en "zone de combat": une période de turbulences extrêmes ☀️

Les rhumatismes plus douloureux par temps humide: vrai ou faux ? 🌧️

Ce nouveau type de moteur repousse les limites du vol supersonique ✈️

Poster sur les réseaux sociaux peut nuire à votre santé mentale 🧠

Une super-Terre entre Mars et Jupiter ? 🌎

Découverte impressionnante d'un fossile de crocodile géant 🐊

Cet accident en laboratoire pourrait transformer drastiquement la mémoire numérique ⚡

Un virage technologique révèle l'impact du diabète gestationnel 🩺

Insolite: ces loups butinent des fleurs ! Des grands carnivores pollinisateurs ? 🌼

Ce fin gilet robotisé soulage les tâches répétitives 🦾

Les équations d'Einstein invalidées ? 👀

Ce tatouage électronique se connecte à votre cerveau 🧠

Cette IA de Google prédit la météo mieux que jamais, et sur 15 jours ! 🌦️

Des plats au bœuf... sans bœuf ? 🥩

Ce moteur de recherche d'un nouveau genre bouscule nos habitudes 🔍

Pourquoi les cheveux bouclent-ils en fonction de la météo ? 🌦️

Découverte: d'autres univers plus propices à la vie que le notre 👽

Ces sons urbains qui minent notre santé mentale 🚗

La testostérone impacte-t-elle vraiment le désir sexuel des hommes ? 🔥

Des microalgues éliminent les métaux lourds: voici comment 🧪

Et voici un qubit mécanique ! 🖥️

Les lentilles de contact sont-elles vraiment sans danger ? 👁️

Dans la course à l'IA générative, Google lance son générateur de vidéos 🎥

Une zone oubliée du cerveau permet aux paralysés de marcher à nouveau 🧠

Cette astuce quotidienne ajoute 11 ans à votre vie 🕒

Page générée en 0.273 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales | Partenaire: HD-Numérique
Version anglaise | Version allemande | Version espagnole | Version portugaise