Modèle d'Ising - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - État fondamental - Deux dimensions - Une dimension - Quatre dimensions et plus - Trois dimensions - Fonction de partition d'une chaine de spins d'Ising en champ moyen avec interaction entre premiers voisins - Fonction de partition d'un ensemble de spins d'Ising en champ moyen sans interaction entre premiers voisins - Intérêt du modèle

Introduction

Le modèle d'Ising (parfois aussi appelé modèle de Lenz-Ising), dénommé d'après le physicien Ernst Ising, est un modèle de physique statistique. Il a été utilisé pour modéliser différents phénomènes dans lesquels des effets collectifs sont produits par des interactions locales entre particules à deux états, comme le ferromagnétisme.

Le modèle d'Ising est un modèle sur réseau de moments magnétiques de particules ayant pour propriétés spécifiques d'être toujours orientés suivant le même axe spatial et de ne prendre que deux valeurs possibles, +M et -M. Ce modèle permet de décrire relativement simplement le magnétisme des matériaux ferromagnétiques présentant une anisotropie très forte avec une direction privilégiée très marquée. Une autre application du modèle d'Ising est la description des alliages binaires. Dans ce cas, les moments magnétiques +M représentent une des espèces atomiques, et les moments magnétiques -M représentent l'autre espèce atomique. L'ordre à longue distance du modèle d'Ising peut décrire une séparation de phase entre les deux espèces (dans le cas où la phase de basse température à tous les moments égaux à -M ou +M) ou bien une phase ordonnée dans laquelle l'un des sous réseaux porte des atomes d'une espèce (moments +M) et l'autre sous réseau des atomes de l'autre espèce. La phase désordonnée du modèle d'Ising décrit respectivement un état où les deux espèces se mélangent ou un état où les sous-réseaux sont équivalents. Le second cas est appelé transition ordre-désordre. Cette version du modèle d'Ising est appelée modèle de Bragg et Williams (1936). Une troisième application de ce modèle est la description d'une transition liquide gaz. Dans cette version, les sites portant un moment +M représentent les sites occupés par un atome, et ceux portant un moment -M les sites inoccupés. Le champ magnétique devient dans cette description le potentiel chimique des atomes. La transition de phase se produisant en présence du champ magnétique, c'est une transition du premier ordre entre un état liquide de forte densité et un état gazeux de faible densité. Cette version du modèle d'Ising est appelée modèle du gaz sur réseau.

Le Hamiltonien de ce modèle s'écrit:

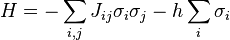
$H=-\sum_{i,j} J_{ij}\sigma_i \sigma_j -h \sum_{i}\sigma_i~$

$J i j$ est l'interaction d'échange du modèle, et $h$ le champ magnétique. En général, on considère le modèle d'Ising avec interaction entre premier voisins seulement.

État fondamental

Dans le cas $J i j > 0$ , l'état fondamental pour $h = 0$ est celui où tous les moments ont la même valeur. Dans le cas $J i j < 0$ sur un réseau bipartite, le fondamental est également facile à trouver, tous les moments ayant sur l'un des sous réseau la valeur $M$ et $- M$ sur l'autre sous réseau. Dans le cas d'un réseau non bipartite, et pour $J i j < 0$ , la situation est plus compliquée toutes les énergies d'interaction entre les moments ne pouvant être minimisées simultanément. Dans ce cas, on dit que le modèle d'Ising est frustré. Pour un modèle d'Ising frustré, le fondamental peut ne pas être unique et peut même avoir une dégénérescence macroscopique (c'est le cas du modèle d'Ising frustré sur le réseau triangulaire en deux dimensions). Dans certains cas, il est possible de calculer exactement la dégénérescence du fondamental (G.H. Wannier, 1950).

Il est également possible de considérer des modèles d'Ising avec des interactions aléatoires (modèle d'Edwards-Anderson si les interactions sont à courte portée, modèle de Sherrington et Kirkpatrick si les interactions sont à longue portée). Ces modèles décrivent des matériaux dans lesquels des impuretés magnétiques ont été diluées dans un métal. La frustration empêche ces modèles de développer un ordre à longue portée conventionnel, et joue un rôle important dans la formation d'un état verre de spin.