Modèle d'Ising - Définition

Une dimension

À une dimension, le modèle d'Ising est exactement soluble par la méthode de la matrice de transfert. Historiquement, cette solution remonte à la thèse d'Ising (1925) sous la direction de Lenz. Cette solution montre que l'énergie libre est analytique pour toute température, ce qui signifie que ce modèle ne possède pas de transition de phase. Un argument physique très général, exposé dans Landau et Lifshitz, permet de montrer que tout modèle unidimensionel avec des interactions à courte portée ne peut pas posséder de transition de phase à température positive, l'énergie nécessaire pour créer des défauts étant toujours largement contrebalancée par le gain d'entropie. F. J. Dyson a étudié des modèles d'Ising avec interaction à longue portée en une dimension, tels que J_ij = | i − j | ^{− σ}. Il a montré que pour σ < 2 ces modèles étaient ordonnés à toute température et pour σ > 2 ces modèles étaient désordonnés à toute température. Seul le cas σ = 2 pouvait éventuellement donner lieu à une transition de phase. Le travail ultérieur de P.W. Anderson, A. Yuval et D. R. Hamman sur l'effet Kondo a montré qu'il existait une relation entre le modèle d'Ising à longue portée avec σ = 2 et l'effet Kondo. Le modèle avec σ = 2 peut donc présenter une transition de phase, qui présente des analogies avec la transition de Berezinsky, Kosterlitz et Thouless.

Quatre dimensions et plus

Bien que ce cas soit non physique, les exposants critiques du modèle d'Ising sont alors ceux de la théorie de champ moyen. Dans le langage du groupe de renormalisation, quatre est la dimension critique supérieure du modèle d'Ising. Il est également intéressant de noter que la théorie de champ moyen est la solution exacte d'un modèle d'Ising à portée infinie défini par le hamiltonien:

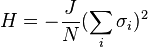
Formellement, ce modèle décrit un moment magnétique interagissant avec un nombre de voisins qui tend vers d'infini. Il peut donc être vu comme la limite de dimension infinie du modèle d'Ising. Si au lieu de définir le modèle d'Ising en dimension infinie à l'aide d'une interaction de portée infinie, on fixe le nombre de voisins en considérant un modèle sur un arbre de Cayley (appelé aussi réseau de Bethe), on trouve que la solution exacte est donnée par l'approximation de Bethe-Peierls. Cette approximation donne une meilleure estimation de la température comparée au champ moyen, mais comme il s'agit aussi d'une méthode autocohérente, elle reproduit les exposants de champ moyen.

Trois dimensions

Pour le modèle d'Ising à trois dimensions, on n'a pas encore trouvé de solution analytique. Cependant, il est possible de calculer les exposants critiques du modèle d'Ising près de la transition en utilisant le groupe de renormalisation. Une table de ces exposants peut être trouvée dans le livre de Claude Itzykson et J. M. Drouffe.

On a pu calculer sa température critique via des simulations sur ordinateur (Monte Carlo):

Fonction de partition d'une chaine de spins d'Ising en champ moyen avec interaction entre premiers voisins

La forme la plus simple d'interaction entre les premiers voisins est du type JM_iM_{i + 1} ou J est la constante de couplage. Dans un tel cas, l'énergie impliquée dans l'interaction prend dans le cas de spins d'Ising la valeur JM² ou − JM².L'énergie de l'ensemble de la chaine prend la forme

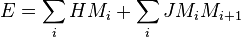
et la fonction de partition prend alors la forme

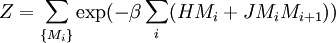
On peut dans ce cas se réduire au problème de spins sans interaction par l'astuce suivante: On remplace les variables M_i par les variables . Il en résulte une factorisation possible de Z:

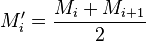
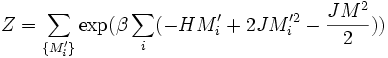
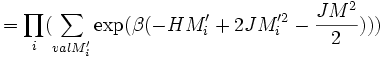
soit encore:

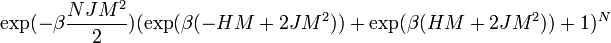
De cette façon on peut encore calculer avec une relative simplicité les diverses variables thermodynamiques.