Modèle d'Ising - Définition
La liste des auteurs de cet article est disponible ici.
Fonction de partition d'un ensemble de spins d'Ising en champ moyen sans interaction entre premiers voisins
Il s'agit du modèle le plus simple. L'énergie de chaque moment ne peut prendre pour valeur que +MH ou -MH, H étant le champ moyen. La fonction de partition prend donc la valeur:
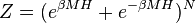
d'où on peut déduire facilement l'aimantation, la susceptibilité magnétique, les grandeurs thermodynamiques, etc.
Intérêt du modèle
Malgré la simplicité du calcul à une dimension, le calcul à deux dimensions nécessite déjà un très gros investissement intellectuel (Onsager !). Quant au calcul exact à trois dimensions par les méthodes traditionnelles, il est impossible. L'extrême simplicité de l'interaction élémentaire permet donc de faire apparaître d'une façon très élégante toute la complexité due à la géométrie du matériau étudié. Si nous ajoutons que le spin d'Ising est un modèle très adapté aux simulations numériques sur ordinateur, nous ne nous étonnerons pas de la popularité d'un modèle apparemment si simple.

















































