Modèle d'Ising - Définition

Deux dimensions

Solution exacte

Dans le cas bidimensionnel, Rudolf Peierls a pu montrer en 1936 que le modèle d'Ising possédait une transition de phase. Des arguments théoriques (dualité) dus à Kramers et Wannier ont permis de prédire en 1941 la température à laquelle se produit cette transition de phase. La solution du modèle, en champ nul, au sens du calcul exact de l'énergie libre est due à Lars Onsager en 1944. La méthode d'Onsager généralise la méthode des matrices de transfert au cas bidimensionnel. Elle exige l'étude d'une algèbre de matrices (voir le livre de Kerson Huang). Cette méthode étant très compliquée, d'autres physiciens ont cherché à mettre au point des techniques de résolutions plus simples pour ce modèle. Une approche due à Kauffmann à conduit à mettre le modèle d'Ising à deux dimensions en relation avec un modèle de fermions unidimensionnels sans interactions. Cette approche a été développée par la suite à l'aide de méthodes d'algèbres de Grassmann par Samuel. Elle est décrite dans le livre de C. Itzykson et J. M. Drouffe. Une autre approche due a Kac et Ward (1952) consiste à ramener le calcul de la fonction de partition à une énumération de graphes. Cette approche est décrite dans le livre de Landau et Lifchitz.

Le comportement du paramètre d'ordre en dessous de la température de transition a été conjecturé par Onsager en 1949. La conjecture d'Onsager a été démontrée par C. N. Yang en 1952. Une méthode plus simple, qui utilise les matrices de Toeplitz et le lemme de Szego a été introduite par E. W. Montroll, J. C. Ward et Renfrey B. Potts en 1963. Les fonctions de corrélations ont été obtenues par Tracy, McCoy et Wu en 1976 en termes de fonctions de Painlevé III. Les résultats de Tracy, MacCoy et Wu ne sont pas limités au point critique du modèle d'Ising, mais sont également valables pour le modèle d'Ising non-critique.

D'autre part, la dualité de Kramers-Wannier a été étendue par L. Kadanoff et H. Ceva en 1971, qui ont introduit l' opérateur de désordre μ. Dans la phase de haute température, et . La situation est renversée dans la phase de haute température. La dualité de Kramers-Wannier échange les opérateurs d'ordre et de désordre (et évidemment échange aussi leurs fonctions de corrélation).

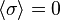
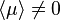
Importance du modèle d'Ising pour le développement de la théorie des phénomènes critiques

L'intérêt du modèle d'Ising vient de ce que ce modèle exactement soluble possède des exposants critiques qui sont différents de ceux donnés par les théories de champ moyen. Par exemple, l'exposant critique de la longueur de corrélation dans le champ moyen est ν=1/2 alors qu'il vaut ν=1 dans le modèle d'Ising. Un autre exemple est l'exposant du paramètre d'ordre qui vaut β=1/8 dans le cas du modèle d'Ising et β=1/2 dans le cas d'une théorie de champ moyen. La solution du modèle d'Ising bidimensionnel a ainsi permis de montrer que la mécanique statistique était capable de prédire les transitions de phase et de décrire des comportements critiques plus complexes que celui des théories de champ moyen. Cela a ouvert la voie aux travaux ultérieurs de M. E. Fisher, L. P. Kadanoff et H. Widom sur l'hypothèse d'universalité et l'invariance d'échelle près du point critique dans les années 1960. En particulier, le modèle d'Ising satisfait aux relations entre exposants critiques résultant de l'hypothèse d'homogénéité de Widom ainsi qu'à la relation d'hyperscaling. La mise au point du groupe de renormalisation pour les transitions de phases dans les années 1970 a ensuite permis de justifier ces hypothèses.

Invariance conforme du modèle d'Ising

Comme de nombreux autres modèles bidimensionnels, le modèle d'Ising au point critique possède la propriété d'invariance conforme, avec la charge centrale c = 1 / 2.

Cette propriété permet de calculer exactement au point critique toutes les fonctions de corrélation à n-points (et non uniquement les fonctions à deux points). Par ailleurs, l'invariance conforme permet aussi de construire un algèbre d'opérateurs faisant intervenir l'aimantation σ de poids conforme (1/16,1/16), l'opérateur de désordre de Kadanoff et Ceva μ de poids conforme (1/16,1/16), les opérateurs de Fermions de Kauffmann ψ de poids conformes (1/2,0) et (0,1/2) et l'opérateur de densité d'énergie ε de poids conforme (1/2,1/2). On a les relations:

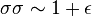
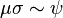
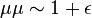
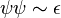
où les produits sont compris comme des développements de produits d'opérateurs. Cet algèbre peut se généraliser pour conduire aux théories conformes parafermioniques. Le modèle d'Ising peut aussi être obtenu à partir des modèles de Wess-Zumino-Witten par une procédure de quotient. Le modèle d'Ising est le quotient .

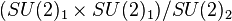
La théorie conforme du modèle d'Ising peut être perturbée par un opérateur de la forme hσ(x). A.B. Zamolodchikov a pu montrer que cette théorie perturbée était intégrable, et il a pu conjecturer la matrice S de la théorie des champs massive décrivant le modèle perturbé.

Le fait que le modèle d'Ising possède la charge centrale c = 1 / 2 permet de ramener le modèle d'Ising double à une théorie de charge centrale c = 1 qui peut être décrite comme un orbifold de théorie de boson libre.