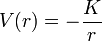Moment angulaire - Définition

Exemples d'application

Mouvement à force centrale : cas général

Un cas particulier très important d'utilisation du moment cinétique est celui du mouvement à force centrale, où le point matériel M est soumis à une seule force dont la direction passe par un point fixe dans (R), appelé centre de force. Par suite en prenant ce centre de force pour origine O, le théorème du moment cinétique (3) implique que le moment cinétique est une intégrale première du mouvement : , soit , puisque et sont colinéaires.

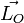
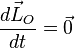
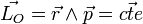
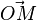
Par conséquent le vecteur position et la quantité de mouvement du corps sont à tout instant perpendiculaires à un vecteur de direction constante : la trajectoire est donc plane, entièrement contenue dans le plan perpendiculaire à (l'indice "0" désigne les valeurs initiales des grandeurs).

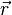
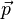
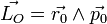
Le mouvement ne comportant que deux degrés de liberté on se place en coordonnées polaires (r,θ) dans le plan de la trajectoire. Il vient ainsi :

, avec constante.

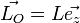
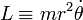
Compte tenu de en coordonnées polaires, l'énergie cinétique du point matériel peut se séparer en une partie radiale et une partie angulaire. Elle s'écrit alors .

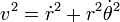
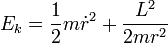
Mouvement à force centrale : cas où la force dérive d'une énergie potentielle

Si la force centrale dérive d'une énergie potentielle V(r), l'énergie mécanique du corps se met sous la forme: avec , énergie potentielle effective.

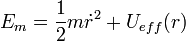
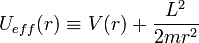
On se ramène à un mouvement unidimensionnel d'une particule fictive dans un potentiel U_eff(r). Le terme étant positif et croissant à courte distance, il joue le rôle de "barrière de potentiel centrifuge".

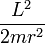
Quelques remarques et références additionnelles

1. De nombreux auteurs supposent qu'une force centrale dérive toujours d'une énergie potentielle : ceci est faux en général. Par exemple, pour le pendule simple, la force de tension du fil est une force centrale car elle passe toujours par le point de fixation O du pendule, MAIS elle ne dérive pas d'une énergie potentielle (à moins de considérer l'état microscopique des atomes composant le fil, dont l'énergie potentielle augmente bel et bien).
2. Une application importante des développements précédents est dans l'étude du mouvement keplerien des planètes et des satellites. Les trajectoires sont alors des courbes fermées — des ellipses.
3. Il convient de souligner qu'en général les trajectoires obtenues pour une énergie potentielle V(r) quelconque ne sont pas des courbes fermées : seuls le potentiel coulombien attractif (K constante) et le potentiel harmonique V(r) = αr² en donneront (Théorème de Bertrand). Cela provient de l'existence, pour ces potentiels, d'une intégrale première additionnelle ( démonstration ? ) (pour le potentiel coulombien, il s'agit du vecteur de Runge-Lenz), associé à une symétrie supplémentaire (par transformation du groupe O(4)).