Nicolas Bourbaki - Définition

Héritage et influence

En mathématique

Ce que les mathématiques doivent à Bourbaki est essentiellement :

• un style, une façon d'écrire les mathématiques ;
• la vulgarisation en France des symboles ∀ et ∃ (l'un venant de Gentzen et l'autre de Peano) ;
• la vulgarisation du symbole ∅ introduit par André Weil et Claude Chevalley ;
• l'utilisation des symboles ⇐, ⇒ et ⇔ en logique ;
• la vulgarisation du lemme de Zorn ;
• la notion de structure ;
• la vulgarisation du symbole pour désigner le produit tensoriel et l'introduction du terme « algèbre multilinéaire » ;
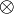
• les termes partition, surjectif, injectif, boule, noethérien, artinien, factoriel ;
• les notions de « filtre » et d'« ultrafiltre » ;
• le terme « forme sesquilinéaire »
• l'introduction des termes « chambre » et « appartement » en théorie des immeubles de Tits et l'introduction des BN-paires en théorie des groupes de Lie ;
• une certaine attention à l'histoire des mathématiques développée dans quelques « notes » accompagnant la parution des Éléments.

On est redevable à Bourbaki d'un travail de clarification des concepts, de précision dans la formulation, d'une recherche — parfois aride — de structure, de classification systématique et exhaustive des mathématiques.

Dans d'autres disciplines

En littérature, l'Oulipo copie indéniablement la « méthode » Bourbaki de travail collectif et de mise en évidence systémique des structures profondes de la création littéraire. À noter qu'un membre important de l'Oulipo, Jacques Roubaud est un mathématicien qui a été très marqué par Bourbaki. C'est par exemple lui qui a écrit l'avis de décès de Bourbaki, sous forme de canular.

Le structuralisme lacanien ou celui de Lévi-Strauss en ethnologie, à la même époque, dénote d'une quête de structures fondamentales dont on peut débattre s'il s'agit de l'influence de Bourbaki ou d'un certain « air du temps ».

Le philosophe des sciences Jules Vuillemin fut influencé par Bourbaki (La philosophie de l'algèbre).

Note critique

Il est inutile d'imaginer un groupe qui ait influencé les autres groupes. André Weil (1906) est sensiblement de la même génération qu'André Breton (1896), Jacques Lacan (1900), ou Claude Lévi-Strauss (1908). Tous ces groupes avaient atteint leur apogée en 1964.

Une rencontre s'est opérée géographiquement au mois de janvier 1964 lorsque le directeur de l'École normale, Robert Flacelière a mis à la disposition de Jacques Lacan une salle dans les locaux de son école. (Séminaire Livre XI, Les Quatre concepts fondamentaux de la psychanalyse).

D'un côté Jacques Lacan souhaitait la venue des mathématiciens pour formuler les structures algébriques et topologiques qu'il considérait à l'œuvre dans la psychanalyse ; de l'autre les mathématiciens voyaient là, peut-être avec un certain amusement, une application concrète des mathématiques fondamentales.

C'est sensiblement à cette époque que le groupe Bourbaki fit paraître la Théorie des ensembles dont Lacan fit un très grand usage.

Ce qui distinguerait le groupe des mathématiciens des autres groupes, ce serait son côté fermé et réservé aux mathématiciens de haut niveau de l'École normale supérieure, alors que le structuralisme prétendrait intéresser tous les praticiens des sciences humaines : littérature, politique, psychanalyse, ethnologie, linguistique.

Il y a bien sûr un point commun, qui est le retour aux sources, la recherche des fondements et la rupture épistémologique.

Mais les deux groupes sont néanmoins restés sur leur quant-à-soi.