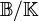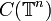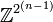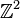K-théorie - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématique, la K-théorie est un outil utilisé dans plusieurs disciplines. En topologie algébrique, la K-théorie topologique (en) sert de théorie de cohomologie. Une variante est utilisée en algèbre sous le nom de K-théorie algébrique (en).
Les premiers résultats de la K-théorie ont été dans le cadre de la topologie algébrique, comme une théorie de cohomologie extraordinaire (elle ne vérifie pas l'axiome de dimension). Après ses méthodes ont été utilisées dans beaucoup de sujets comme la géométrie algébrique, l'algèbre, théorie des nombres, théorie des opérateurs, etc.
Histoire
C'est Alexandre Grothendieck qui a fait la première construction d'un groupe de K-théorie dans son travail sur le théorème maintenant connu comme théorème de Grothendieck-Riemann-Roch. Il a introduit la complétion du monoïde de faisceaux de groupes abéliens avec la somme directe en utilisant des inverses formels. Cette idée a été reprise par Michael Atiyah et Friedrich Hirzebruch (en) pour définir le groupe K(X) d'un espace topologique, en faisant la même construction pour les classes d'isomorphisme de fibrés vectoriels. Cette construction a été la première théorie cohomologique extraordinaire en topologie algébrique. Son utilisation a été fondamentale pour la démonstration du célèbre « théorème de l'indice » de M. F. Atiyah et I. Singer, travail qui a fait obtenir à ses auteurs la Médaille Fields en 1966.
Par ailleurs, Jean-Pierre Serre s'est appuyé sur l'analogie entre fibrés vectoriels et modules projectifs sur un anneau pour fonder la K-théorie algébrique en 1959. Ceci l'a conduit à énoncer la conjecture de Serre : Tout module projectif sur un anneau de polynômes d'un corps est un module libre. Cette conjecture a été prouvée en 1976, par Daniel Quillen et Andrei Suslin (en) en utilisant des méthodes de K-théorie algébrique. Quillen a ensuite donné une définition satisfaisante des foncteurs Kn, en utilisant de la théorie homotopique.
Catalogue de groupes élémentaires de K-théorie topologique
| A | K0(A) | K1(A) |
|---|---|---|
|
|
| 0 |
|
|
| 0 |
|
|
| 0 |
|
| 0 | 0 |
|
| 0 |
|
|
|
| 0 |
| 0 |
| |
|
|
|
|
| C(S2n) |
| 0 |
| C(S2n + 1) |
|
|
| Aθ |
|
|
où
-
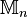
-

-
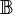
-
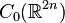
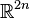
-
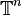
- Sn est la sphère de dimension n ;
- Aθ est le tore non-commutatif associé au nombre irrationnel θ.
Notons que le tore non-commutatif et le tore (commutatif) de dimension 2 ont la même K-théorie.
La notion de tore non-commutatif se généralise facilement aux dimensions supérieures. Ces tores non-commutatifs de dimensions supérieures ont la même K-théorie que leurs analogues commutatifs.
Périodicité de Bott
-
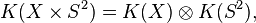
![K(S^2)=\mathbb Z[H]/(H-1)^2;](https://static.techno-science.net/illustration/Definitions/autres/5/58479c3c2a7574c5ca84b747a02fe3cb_5105cd864fb2d8d8536953a1baf30ad5.png)
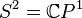
-
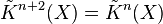
-
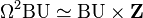
K-théorie et physique
En théorie des cordes, la K-théorie a fourni une bonne description des charges permises de D-branes.
Fondateurs
- Alexandre Grothendieck
- Michael Atiyah
- Friedrich Hirzebruch (en)
- Jean-Pierre Serre
- Max Karoubi
- Daniel Quillen