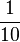Nombre p-adique - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En théorie des nombres, si p est un nombre premier, un nombre p-adique est un objet mathématique qui peut se concevoir comme une suite de chiffres en base p, éventuellement infinie à gauche de la virgule (mais toujours finie à droite de la virgule). Avec une addition et une multiplication qui se calculent comme pour les nombres décimaux usuels, l'ensemble des nombres p-adiques forme un corps noté

Chaque corps


La principale motivation ayant donné naissance aux corps des nombres p-adiques était de pouvoir utiliser les techniques des séries entières dans la théorie des nombres, mais leur utilité dépasse maintenant largement ce cadre. De plus, la norme p-adique sur le corps

Construction
Approche analytique
Les nombres réels sont définis comme des classes d'équivalence des suites de Cauchy des nombres rationnels. Cependant, cette définition repose sur la métrique choisie et, en en choisissant une autre, d'autres nombres que les nombres réels peuvent être construits. La métrique utilisée pour les nombres réels est appelée métrique euclidienne.
Pour un nombre premier donné p, on définit la norme p-adique sur
- on appelle valuation p-adique d'un entier a non nul (et l'on note vp(a)) l'exposant de p dans la décomposition de a en produit de facteurs premiers.
- on peut alors construire une valuation pour tout nombre rationnel non nul en posant :
-
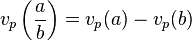
-
- On prouve aisément que cette définition est indépendante du représentant du rationnel choisi.
- La norme p-adique | r | p d'un rationnel r non nul vaut
- Si r est nul, on pose | r | p = 0. Ce prolongement est compatible avec l'idée que 0 est divisible par pk pour toute valeur de k, donc que la valuation de 0 serait infinie.
En quelque sorte, plus r est divisible par p, plus sa norme p-adique est petite (c'est un cas particulier de valuation discrète, un outil algébrique).
Par exemple, pour
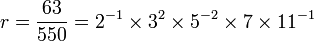
-
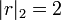
-
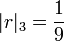
-
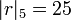
-
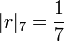
-
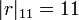
-
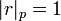
On démontre que cette application a toutes les propriétés d'une norme. On peut montrer que toute norme (non-triviale) sur
- dp(x,y) = | x − y | p
Le corps

Cette construction permet de comprendre pourquoi


Quelques différences analytiques entre




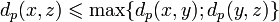
pour tous x,y,z dans

- tout triangle est isocèle,
- toute boule est centrée en n'importe lequel de ses points,
- deux boules sont soit incluses l'une dans l'autre, soit disjointes,
- dans

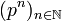
- si dans

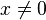
- une suite (un) est de Cauchy si et seulement si
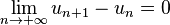
- une série Σ(an) converge si et seulement si
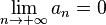
- il n'y a pas d'ordre de corps sur

-

- etc.
Approche algébrique
Dans cette approche algébrique, on commence par définir l'anneau des entiers p-adiques, puis par construction le corps des fractions de cet anneau pour obtenir le corps des nombres p-adiques.
On définit l'anneau des entiers p-adiques
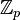
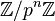
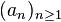
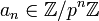
Par exemple, 35 en tant que nombre 2-adique serait la suite
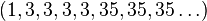
Explication : 35 = 1 + 21 + 25 qu'on peut écrire aussi
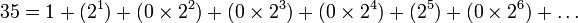
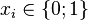
a1 = 1,
a2 = 1 + 2 = 3,
a3 = 1 + 2 + 0 = 3,
a4 = 1 + 2 + 0 + 0 = 3,
a5 = 1 + 2 + 0 + 0 + 0 = 3,
a6 = 1 + 2 + 0 + 0 + 0 + 0 + 25 = 35, etc.
On a bien, pour tout n,
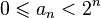
![a_n = a_{n+1}\ [2^n]](https://static.techno-science.net/illustration/Definitions/autres/4/4b7d6378813810e0dd507094534ff553_5f0cca34a6e09320fdd0c41df7cc2947.png)
L'addition et la multiplication de telles suites sont bien définies, puisqu'elles commutent avec l'opérateur modulo (voir arithmétique modulaire). De plus, toute suite (an) dont le premier élément n'est pas nul a un inverse.
L'anneau des entiers p-adiques ne possédant pas de diviseurs de zéro, il est possible de considérer son corps des fractions pour obtenir le corps

On montre facilement que

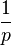
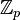
![\mathbb Q_p = \mathbb Z_p [{ \frac{1}{p}}]](https://static.techno-science.net/illustration/Definitions/autres/5/53ea1c25bfda27fb3b1bd47e3d4ddac7_01adf1d3da8af48330528ef8eb4bf47b.png)