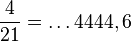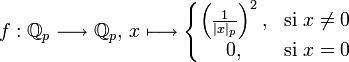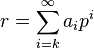Nombre p-adique - Définition

Propriétés

Dénombrabilité

L'ensemble des entiers p-adiques n'est pas dénombrable.

Les nombres p-adiques contiennent les nombres rationnels et forment un corps de caractéristique nulle. Il n'est pas possible d'en faire un corps ordonné.

Topologie

La topologie sur l'ensemble des entiers p-adiques est celle de l'ensemble de Cantor ; la topologie sur l'ensemble des nombres p-adiques est celle de l'ensemble de Cantor privé d'un point (qui serait naturellement appelé infini). En particulier, l'espace des entiers p-adiques est compact, tandis que l'espace des nombres p-adiques ne l'est que localement. En tant qu'espaces métriques, les entiers et les nombres p-adiques sont complets.

Les nombres réels n'ont qu'une seule extension algébrique propre, les nombres complexes. En d'autres termes, cette extension quadratique est algébriquement close. En revanche, la clôture algébrique des nombres p-adiques est de degré infini : les corps ont une infinité d'extensions algébriques non équivalentes. De plus, la clôture algébrique d'un n'est pas complète. Sa complétion métrique est appelée Ω^p et elle est algébriquement close.

Le corps Ω^p, aussi noté , est abstraitement isomorphe au corps des nombres complexes et il est possible de considérer le premier comme le dernier, muni d'une métrique exotique. Cependant, l'existence d'un tel isomorphisme est une conséquence de l'axiome du choix et il n'est pas possible d'en expliciter un.

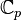
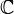
Les nombres p-adiques contiennent le n^e corps cyclotomique si et seulement si n divise p − 1. Par exemple, les 1^er, 2^e, 3^e, 4^e, 6^e et 12^e corps cyclotomiques sont des sous-corps de .

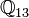
Le nombre e (défini par la série ) n'est élément d'aucun des corps p-adiques. Cependant, e^p (défini par la série ) est un nombre p-adique (sauf si p = 2, mais e⁴ est un nombre 2-adique), aussi e, défini comme une racine p-ème de e^p, est un élément de la clôture algébrique de n'importe quel corps p-adique ; ainsi quel que soit p, e appartient à .

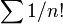
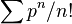
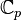
Sur les nombres réels, les seules fonctions dont les dérivées sont nulles sont les fonctions constantes. Ceci n'est pas vrai sur les nombres p-adiques. Par exemple, la fonction

possède une dérivée nulle en tous points, mais n'est même pas constante localement en 0.

Si on se donne les éléments respectivement membres de , il est possible de trouver une suite (x_n) de telle que la limite des x_n dans soit r et, pour tout p premier, elle soit r_p dans .

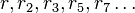
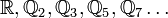
Rationalité

Un nombre positif γ₀ est rationnel si, et seulement si, son développement p-adique est périodique à partir d'un certain rang, c'est-à-dire, s'il existe 2 entiers et k > 0 tel que (La suite a_n représentant le développement p-adique du nombre γ₀)

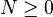
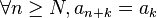
Décomposition canonique de Hensel

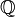
Soit p un nombre premier. Tout élément non nul r de (et en particulier tout élément de ) s'écrit de manière unique sous la forme :

où et les a_i sont des nombres entiers compris entre 0 et p − 1. Cette écriture est la décomposition canonique de r comme nombre p-adique.

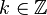
Cette série est convergente suivant la métrique p-adique.

On note l'ensemble des éléments de tels que et on l'appelle ensemble des entiers p-adiques. est un sous-anneau de . On peut représenter un entier p-adique par une suite infinie vers la gauche de chiffres en base p, tandis que les autres éléments de , eux, auront un nombre fini de chiffres à droite de la virgule. Cette écriture fonctionne en somme à l'inverse de ce qu'on a l'habitude de rencontrer dans l'écriture des nombres réels.

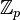
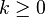
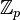
Par exemple, avec p = 2 :

• (le 2 en indice indiquant qu'il s'agit du développement 2-adique de 1)
•  : on peut vérifier que, puisque , ajouter 1 à cette écriture conduit à décaler une retenue tout le long de l'écriture, pour finalement donner 0.
• 
•  : en multipliant ce résultat par , on retrouve 1. On remarque que est un entier 2-adique (i.e. ), mais on le savait déjà en regardant sa valuation : .
• représente un élément de (et même de ) qui n'est pas dans .
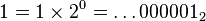
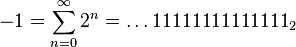
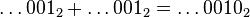
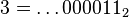
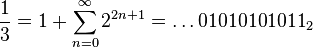
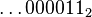
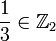
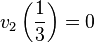
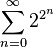
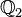
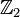
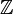
• Le polynôme 2X² + X + 2 se factorise dans sous la forme (X − a)(2X − b) avec et , alors qu'il est irréductible dans ou . On a 2a + b = − 1 et ab = 2.

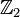
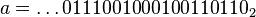
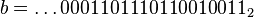
Un autre exemple, avec p = 7 :

2 n'a pas de racine carrée dans mais en possède deux dans , à savoir : et son opposé :

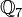
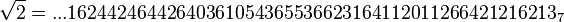
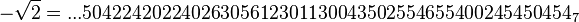
Comment calculer dans

• L'addition est tout à fait similaire à celle de , avec le même système de retenues :

Exemple : dans

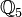
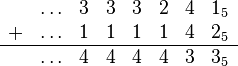
• La multiplication se fait de façon analogue :

Exemple : dans

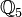
• La division de deux entiers dans .

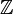
Exemple 1 : Ecrivons dans . Remarquons tout d'abord que car sa valuation 7-adique est 0. Ainsi avec .

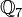
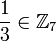
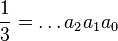
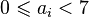
3 est inversible modulo 7 puisque . Ceci permet d'ailleurs d'écrire la relation de Bézout suivante :

d'où :

et à ce stade on a :

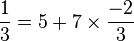
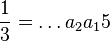
Continuons et multiplions ( * ) par -2 :

et arrangeons pour obtenir des coefficients entre 0 et 6 :

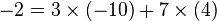
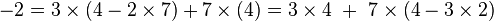
d'où :

et on observe une périodicité puisqu'on retombe sur .

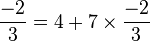
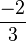
Au bilan : c'est-à-dire : d'où l'écriture 7-adique :

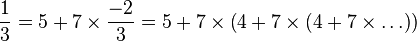
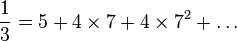
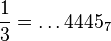
Exemple 2 : Ecrivons dans . Remarquons tout d'abord que car sa valuation 7-adique est -1 : ce sera donc un nombre 7-adique "à virgule".

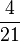
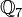
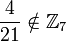
On écrit :

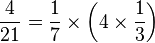
Or on sait que donc en multipliant par 4 :

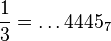
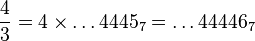
Il ne reste plus qu'à diviser par 7, mais ceci revient à décaler la virgule vers la gauche (on est en base 7) :