Noyau de la chaleur - Définition

Extension aux variétés riemanniennes compactes

Toutes les définitions précédentes s'étendent assez naturellement au cas de l'opérateur de Laplace-Beltrami sur une variété riemannienne compacte, qui possède alors également un spectre discret. Sur une variété compacte, la fonction constante est normalisable à l'unité, de telle sorte que l'état fondamental est associé à la valeur propre nulle, qui est non dégénérée.

Il est alors commode de poser : λ₀ = 0, et on a :

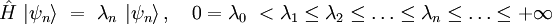
On peut également associer à ce spectre une fonction zêta à la condition de supprimer la valeur propre nulle « à la main ».

Bibliographie

Ouvrages de références

• Marcel Berger, Paul Gauduchon & Edmond Mazet ; Le spectre d'une variété Riemanienne, Lecture Notes in Mathematics 194, Springer-Verlag (1971).
• Isaac Chavel ; Eigenvalues in Riemannian Geometry, Pure and Applied Mathematics 115, Academic Press (2^e édition-1984), ISBN 0121706400.

Quelques articles

• S Minakshisundaram & A Pleijel ; Some properties of the eigenfunctions of the Laplace-operator on Riemannian manifolds, Canadian Journal of Mathematics 1 (1949), 242--256.
• H. P. McKean & I. M. Singer ; Curvature and the eigenvalues of the Laplacian, Journal of Differential Geometry 1 (1) (1967), 43-69.
• Peter B. Gilkey ; The spectral geometry of a Riemannian manifold, Journal of Differential Geometry 10(4) (1975), 601-618.
• Yves Colin de Verdière ; Propriétés asymptotiques de l'équation de la chaleur sur une variété compacte, d'après P. Gilkey, Séminaire Bourbaki (Novembre 1973).
• Yves Colin de Verdière ; Spectre du laplacien et longueurs des géodésiques périodiques (I), Compositio Mathematica 27 (1) (1973), p 83-106. Numdam.
• Yves Colin de Verdière ; Spectre du laplacien et longueurs des géodésiques périodiques (II), Compositio Mathematica, 27 (2) (1973), p 159-184. Numdam.
• Maria Teresa Arede ; Géométrie du noyau de la chaleur sur les variétés, Thèse de troisième cycle, Université de Marseille (1983).
• Teresa Arede ; Manifolds for which the heat kernel is given in terms of geodesic lengths, Letters in Mathematical Physics 9 (2) (1985), 121-131.
• Peter B Gilkey ; Heat Equation Asymptotics, Proc. Symp. Pure and Applied Math. V54 (1993), 317-336.
• Klaus Kirsten ; Spectral functions in mathematics and physics, Chapman & Hall/CRC , Boca Raton, FL (2002), ISBN 1-58488-259-X.
• Peter B. Gilkey ; Asymptotic formulae in spectral geometry, Studies in Advanced Mathematics, vol. 43, Chapman & Hall/CRC, Boca Raton, FL (2004), ISBN 1-58488-358-8

Bibliothèque virtuelle

• Claude Bardos & Olivier Laffite ; Une synthèse de résultats anciens et récents sur le comportement asymptotique des valeurs propres du Laplacien sur une variété riemannienne, (1998). PostScript.
• M. van den Berg, S. Desjardins & P B Gilkey ; Heat content asymptotics of Riemannian manifolds, dans : Differential Geometry and its Applications, O. Kowalski & D. Krupka (éditeurs), proceedings of 5th international conference 1992 on differential geometry and its applications at Silesian University (1993), ISBN 80-901581-0-2, p. 61-64. PostScript.
• D. V. Vassilevich ; Heat kernel expansion: user's manual, Physics Report 388 (2003), 279-360. ArXiv : hep-th/0306138.
• Tamás Hausel ; Eigenvalues and the Heat Kernel, pdf.
• Arlo Caine ; The heat kernel on a Riemannian manifold, pdf.
• Daniel Grieser ; Notes on the heat kernel on manifolds with boundary, pdf.

Articles liés

• Laplacien
• Opérateur de Laplace-Beltrami.
• Géométrie spectrale
• Formule sommatoire de Poisson
• Formule des traces de Selberg
• Formule des traces de Gutzwiller
• Chaos quantique
• Régularisation zêta