Noyau de la chaleur - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le noyau de la chaleur est une fonction de Green, ou solution élémentaire, de l'équation de la chaleur.
Expression et propriétés
Définitions générales
Soit Ω un domaine compact de
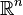
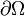
L'opérateur positif
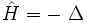
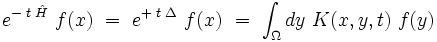
La fonction K(x,y,t) est appelée le « noyau de la chaleur ». En effet, la fonction :
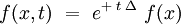
est clairement une solution de l'équation de la chaleur :
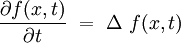
De plus, le semi-groupe tend vers l'identité lorsque le temps t tend vers zéro :
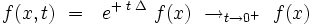
de telle sorte que le noyau de la chaleur K doit avoir le comportement asymptotique :
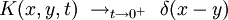
où δ(x) est la distribution de Dirac. Ainsi, le noyau de la chaleur K(x,y,t) apparait comme étant une fonction de Green, ou solution élémentaire, de l'équation de la chaleur.
Théorie spectrale
Lorsque le domaine Ω est compact, l'opérateur positif
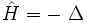
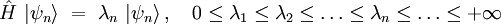
On peut alors écrire en introduisant deux fois la relation de fermeture :
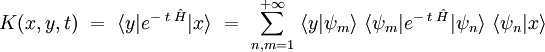
qui devient :
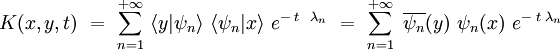
Trace du noyau de la chaleur
La trace du noyau de la chaleur est définie par :
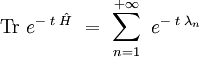
Les états propres étant orthonormés, on remarque que l'on peut écrire :
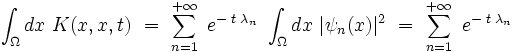
On a donc la relation fondamentale :
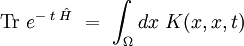
Cette relation est liée à de nombreuses « formules des traces » comme celle de Selberg en géométrie hyperbolique, ou celle de Gutzwiller à l'approximation semi-classique.
Fonctions spectrales
On définit la fonction de comptage des valeurs propres :
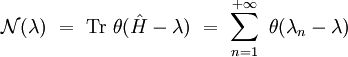
où θ(x) est la distribution de Heaviside. La fonction de comptage est une fonction en escalier positive croissante qui donne le nombre total de valeurs propres inférieures ou égales à λ. Sa dérivée est la densité spectrale de valeurs propres :
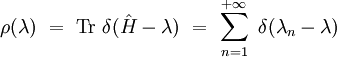
La trace du noyau de la chaleur est reliée à ces fonctions par une transformation de Laplace :
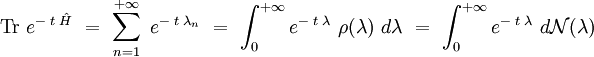
Fonction zeta spectrale
On suppose ici que le fondamental
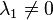
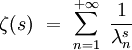
qui converge pour
![\Re \mathrm{e} \left[ \, s \, \right]](https://static.techno-science.net/illustration/Definitions/autres/8/8203ebbccaee87ecdbeb83486dcda8d9_9f85639353df544ad94a78ec206b0523.png)
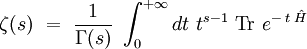
La fonction zêta est notamment utilisée pour régulariser les déterminants d'opérateurs qui apparaissent lors de calculs d'intégrales de chemins en théorie quantique des champs. En effet, le déterminant de l'opérateur H est défini par :
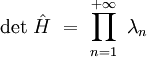
Avec l'identité :
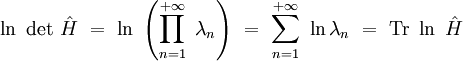
on démontre facilement la relation formelle :
![\mathrm{det} \ \hat{H} \ = \ \exp \, \left[ \, - \ \zeta'(0) \, \right]](https://static.techno-science.net/illustration/Definitions/autres/8/88f67998f9e36e5cfb84cd7e31262a57_a5ed57a6d4a6080e2caa7735d61d0ebe.png)
où la dérivée de la fonction zêta est évaluée en s = 0.
Développement asymtotique du noyau de la chaleur
Le terme diagonal du noyau de la chaleur admet un développement asymptotique en temps petit.
Variété riemannienne compacte sans bord
Pour une variété riemannienne M compacte de dimension d sans bord, on a le développement de Minakshisundaram-Pleijel (1949) :
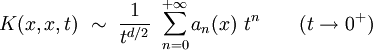
où les coefficients an(x) sont des fonctions lisses sur M, qui dépendent de la métrique et de ses dérivées en x. Par intégration sur tous les points x, on en déduit que la trace du noyau de la chaleur admet également un développement asymptotique en temps petit :
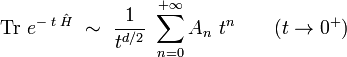
où les constantes An sont définis par :
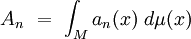
pour le mesure induite par la métrique. Ces constantes font apparaitre certaines caractéristiques géométriques globales de M ; par exemple, la constante A0 est proportionnelle à l'hypervolume de la variété :
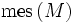
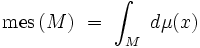
Variétés à bord
L'existence d'un tel développement asymptotique peut être étendu aux variétés à bord suffisamment réguliers. L'opérateur de Laplace-Beltrami doit alors être muni de conditions aux limites appropriées.
Spectre & géométrie
Le développement de la trace du noyau de la chaleur est relié à celui de la fonction de comptage des valeurs propres (ou sa dérivée, la densité spectrale).

















































