Géométrie spectrale - Définition

Introduction

La géométrie spectrale est une branche des mathématiques au carrefour de la géométrie différentielle des variétés riemanniennes et de la théorie spectrale de l'opérateur de Laplace-Beltrami. Plus précisément, il s'agit d'établir des relations entre le spectre des valeurs propres de l'opérateur de Laplace-Beltrami d'une variété riemannienne V compacte avec (ou sans) bords à certaines caractéristiques géométriques (et/ou topologiques) de cette variété.

Cette théorie trouve des applications en physique théorique, notamment pour l'étude de la limite semi-classique de la mécanique quantique, ainsi que pour le chaos quantique.

Peut-on entendre la forme d'un tambour ?

En 1966, Mark Kac a synthétisé un problème typique de géométrie spectrale sous la forme d'une question, devenue célèbre : « Peut-on entendre la forme d'un tambour ? ».

Préhistoire : Debye & Weyl (1911)

Debye

Le physicien Peter Debye s'était intéressé au nombre asymptotique de modes propres de l'équation de Helmholtz pour un « tambourin » Ω rectangulaire de côtés de longueurs respectives a et b, avec des conditions aux limites de Dirichlet :

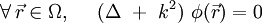
Le problème bidimensionnel admet la solution exacte :

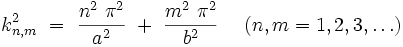
Les valeurs propres inférieures ou égales à λ vérifient :

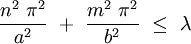
Leur nombre est asymptotique lorsque à :

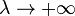
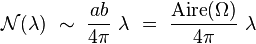
En bon physicien, Debye conjectura que cette formule restait vraie quelle que soit la forme du domaine plan compact, ce que l'expérience semblait confirmer.

Théorème de Weyl (1911)

La conjecture de Debye fût démontré rigoureusement par Weyl en 1911 pour le Laplacien muni de conditions aux limites de Dirichlet. (Le résultat reste vrai avec des conditions aux limites de Neumann.)

Conjecture de Weyl (1911) & théorème d'Ivrii (1980)

Weyl conjectura également que le terme suivant du développement asymptotique de la fonction de comptage des valeurs propres faisait apparaitres le périmètre du bord du domaine :

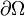
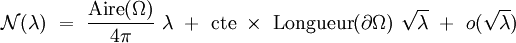
Cette conjecture s'étend en fait naturellement en dimension d quelconque :

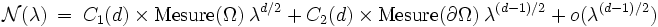
où C₁ et C₂ sont des constantes qui dépendent de la dimension d de l'espace (C₂ dépend aussi des conditions aux limites). Pour une frontière suffisamment régulière, la conjecture de Weyl a été démontrée rigoureusement en 1980 par V. Ja. Ivrii.

Réponse : ça dépend ...

L'exemple de Gordon, Webb et Wolpert (1992) de deux domaines plans non-congruents, pour lesquels les spectres du Laplacien sont identiques. (Les deux domaines possèdent la même aire).

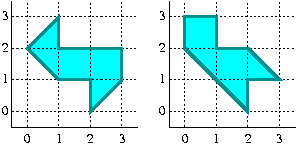
Presque immédiatement après que Kac eut posé sa question, Milnor a exhibé une paire de tores à 16 dimensions ayant le même spectre, mais des formes différentes ! Le problème bidimensionnel n'a été résolu qu'en 1992 par Gordon, Webb et Wolpert. Ils ont construit une paire de domaines plans non-congruents ayant même spectre (cf figure). La démonstration du fait que toutes les valeurs propres sont identiques repose sur l'utilisation des symétries de ces domaines. Cette idée a été généralisée par Buser et al., qui ont construit de nombreux exemples similaires.

La réponse à la question de Kac est donc en général négative : pour la plupart des tambours, on ne peut pas entendre leurs formes complètement, bien que l'on puisse entendre certaines caractéristiques (aire, périmètre, nombre de trous, ...)

En revanche, Zelditch a démontré que la réponse à la question de Kac est positive si l'on se restreint à certaines régions planes convexes dont les frontières sont analytiques. (On ne sait pas si deux domaines non-convexes à frontières analytiques peuvent avoir le même spectre.)

La conjecture de Berry (1979)

Pour un domaine à bord fractal, Berry a conjecturé en 1979 que la correction de bord était proportionnelle à : λ^{D / 2} où D est la dimension de Hausdorff de la frontière. Cette conjecture a été infirmée par J. Brossard et R. A. Carmona, qui ont à leur tour suggéré que la dimension de Hausdorff soit remplacée par la upper box dimension. Sous cette forme, la conjecture a été démontrée en 1993 par Lapidus et Pomerance pour un domaine plan dont la frontière possède une dimension 1, mais infirmée par les mêmes auteurs pour les dimension supérieure en 1996. Des 1993, des contrexemples à cette conjecture ont été démontrés par Jacqueline Fleckinger et Dmitri Vassiliev dans Transactions A.M.S. V337, N.1, may 1993, p.99-116 "An example of a two-term asymptotics for the counting function of a fractal drum". Plusieurs calculs précis ont ensuite été établis par M.Levitin.