Polyèdre quasi-régulier - Définition
La liste des auteurs de cet article est disponible ici.
Définition
Un polyèdre qui possède des faces régulières et qui est transitif sur ses arêtes est dit être quasi-régulier.
Un polyèdre quasi-régulier peut avoir des faces de deux sortes seulement et celles-ci doivent alterner autour de chaque sommet.
On donne un symbole de Schläfli vertical
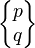
Exemples non-convexes
Coxeter, H.S.M. et.al. (1954) ont classé aussi certains polyèdres étoilés ayant les mêmes caractéristiques et étant quasi-réguliers :
- Deux sont basés sur les solides de Kepler-Poinsot réguliers, de la même manière que les exemples convexes :
- Le grand icosidodécaèdre

- Le dodécadodécaèdre
- Le grand icosidodécaèdre
| Régulier | Dual régulier | Quasi-régulier |
|---|---|---|
 Grand icosaèdre |  Grand dodécaèdre étoilé |

Grand icosidodécaèdre |
 Grand dodécaèdre |  Petit dodécaèdre étoilé |
Dodécadodécaèdre |
- Trois formes ditrigonales, dont les figures de sommet contiennent trois alternements de deux types de faces :
- Le dodécadodécaèdre ditrigonal
- Le petit icosidodécaèdre ditrigonal
- Le grand icosidodécaèdre ditrigonal
| Dodécadodécaèdre ditrigonal | Petit icosidodécaèdre ditrigonal | Grand icosidodécaèdre ditrigonal |
|---|---|---|
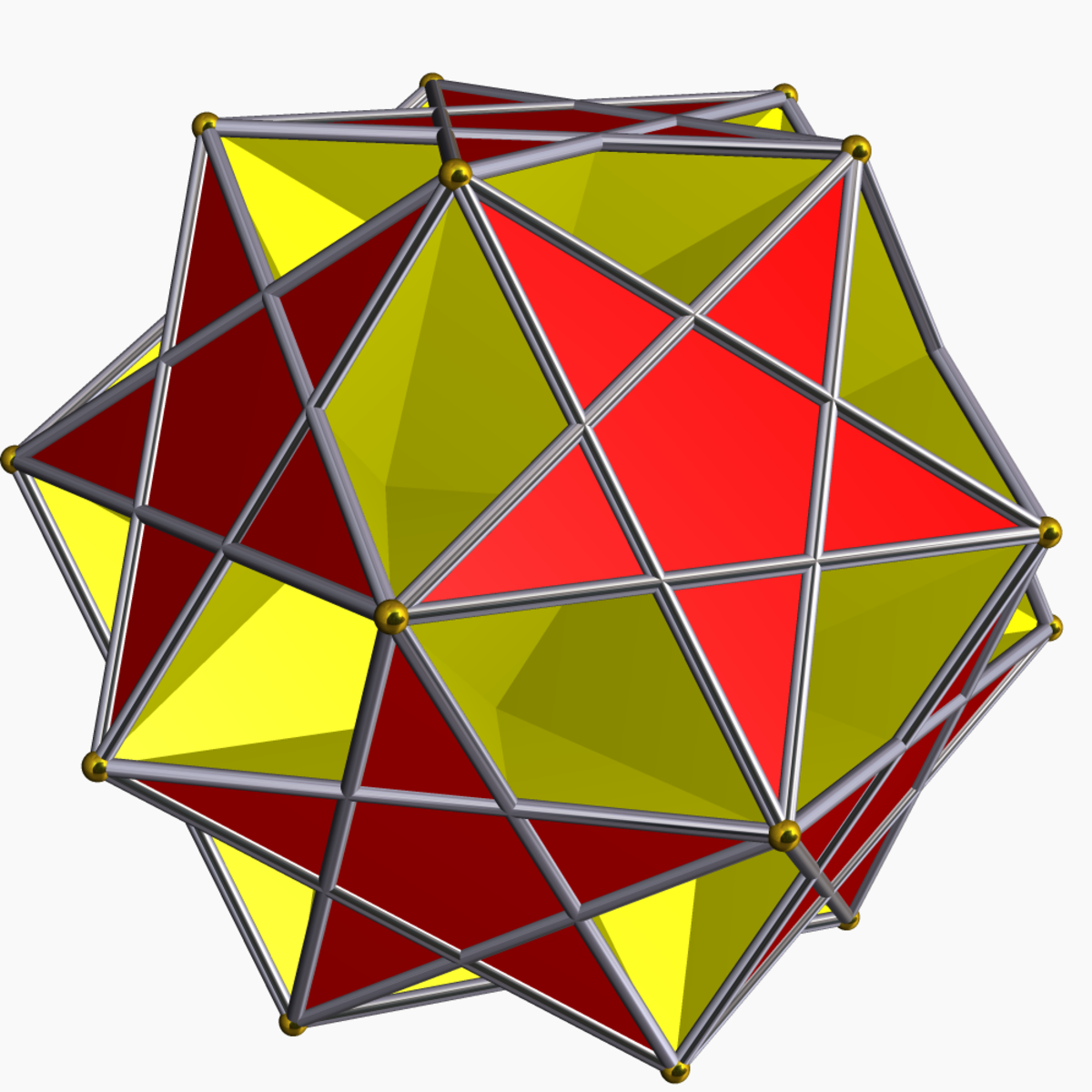
|

|

|
Les polyèdres quasi-réguliers convexes
Il existe trois polyèdres quasi-réguliers convexes :
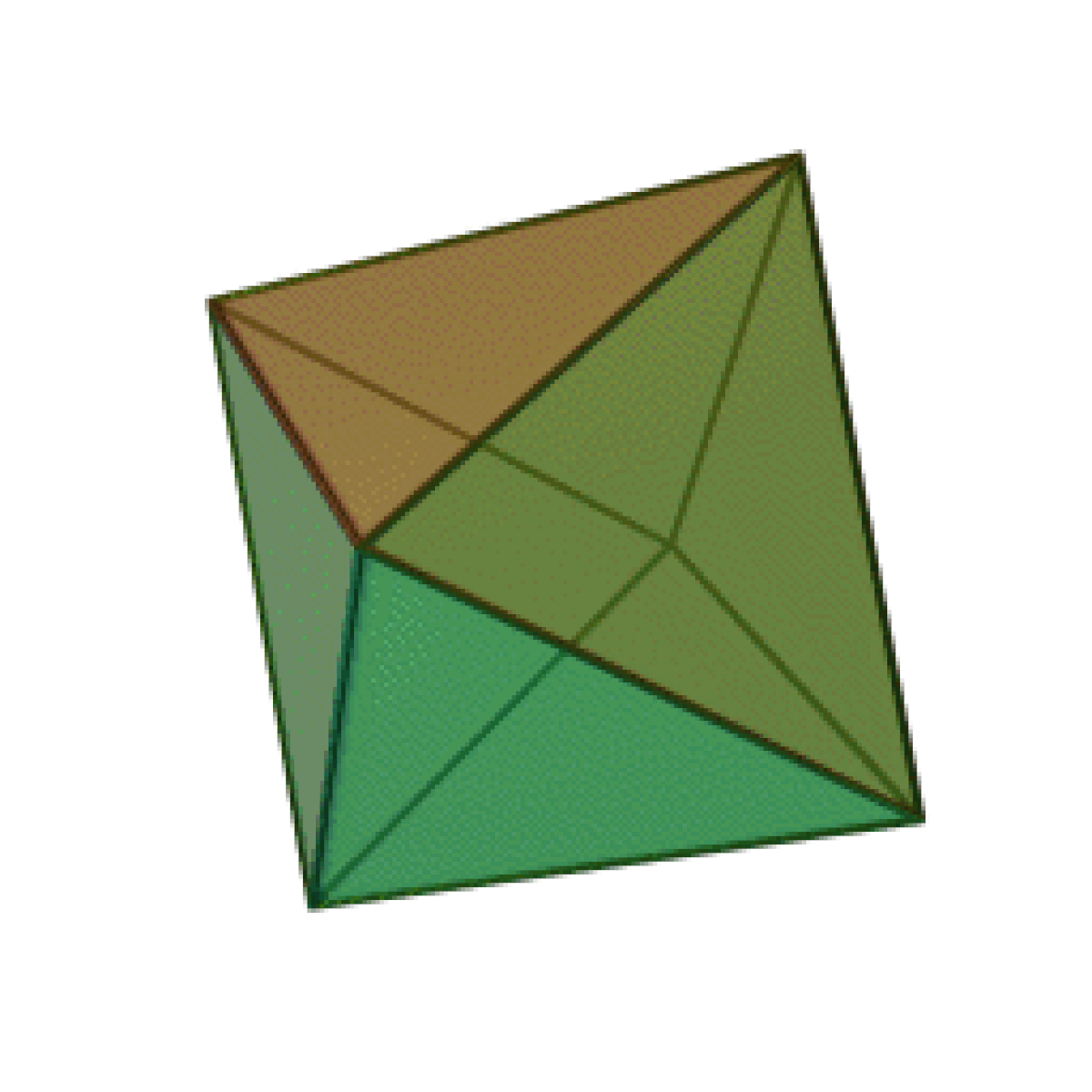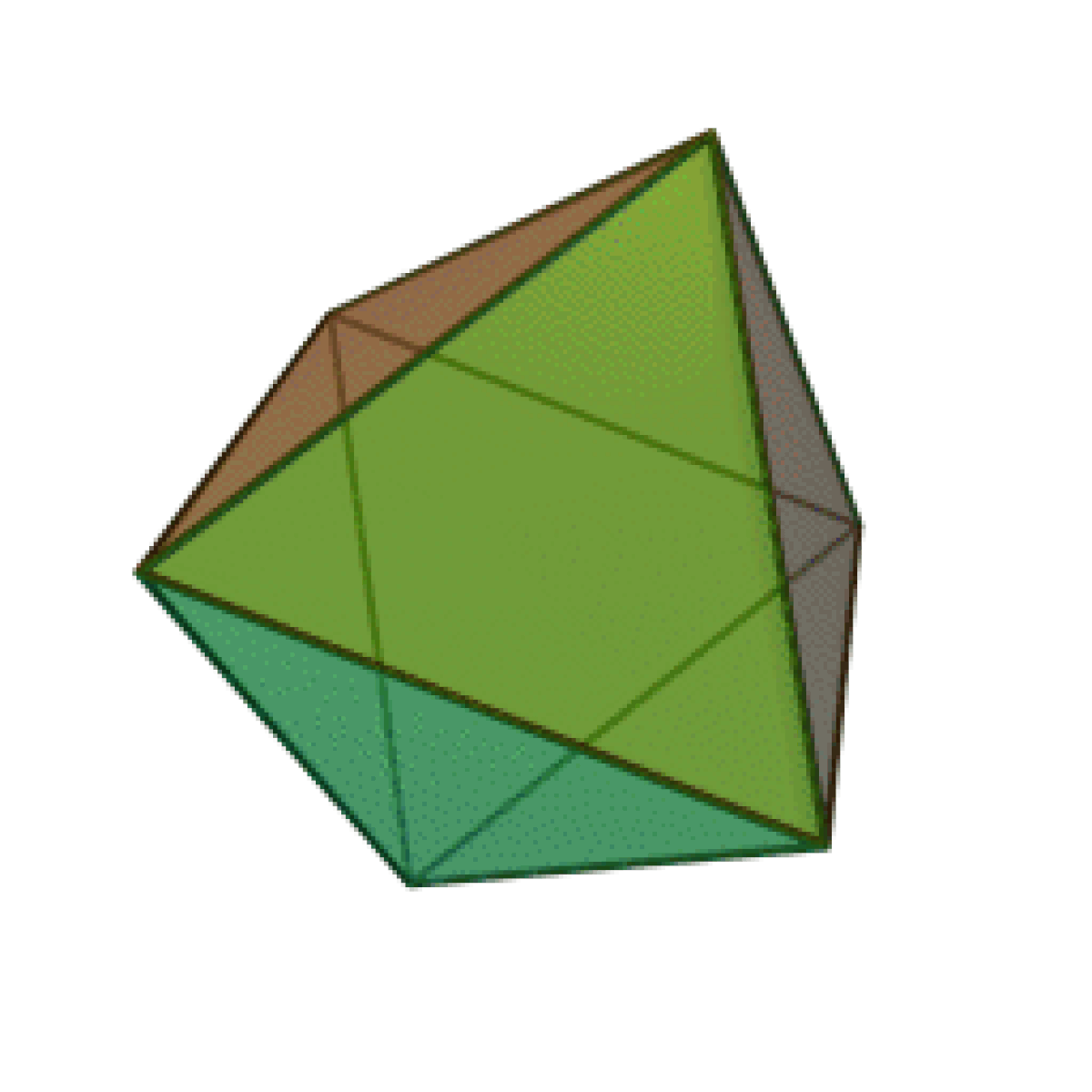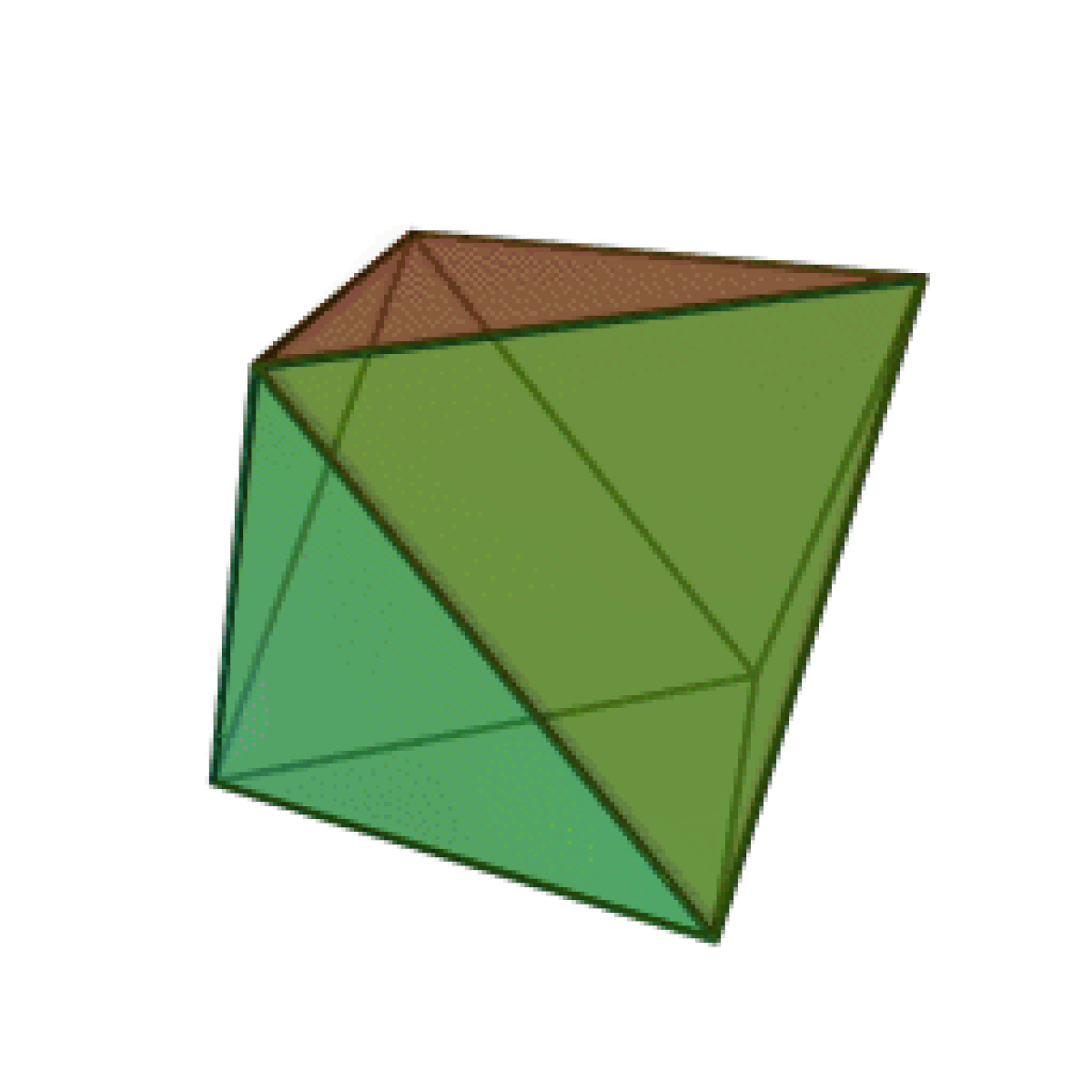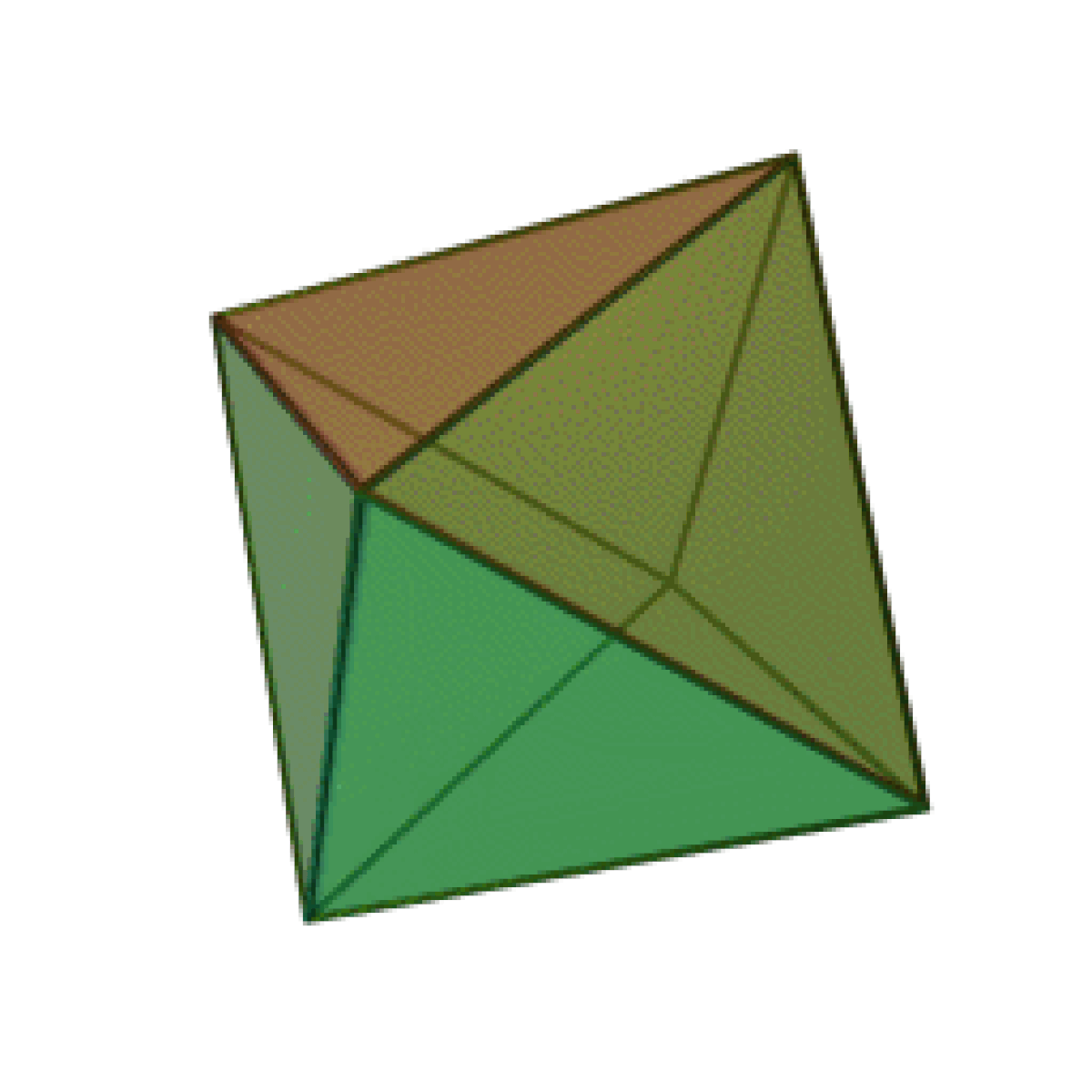
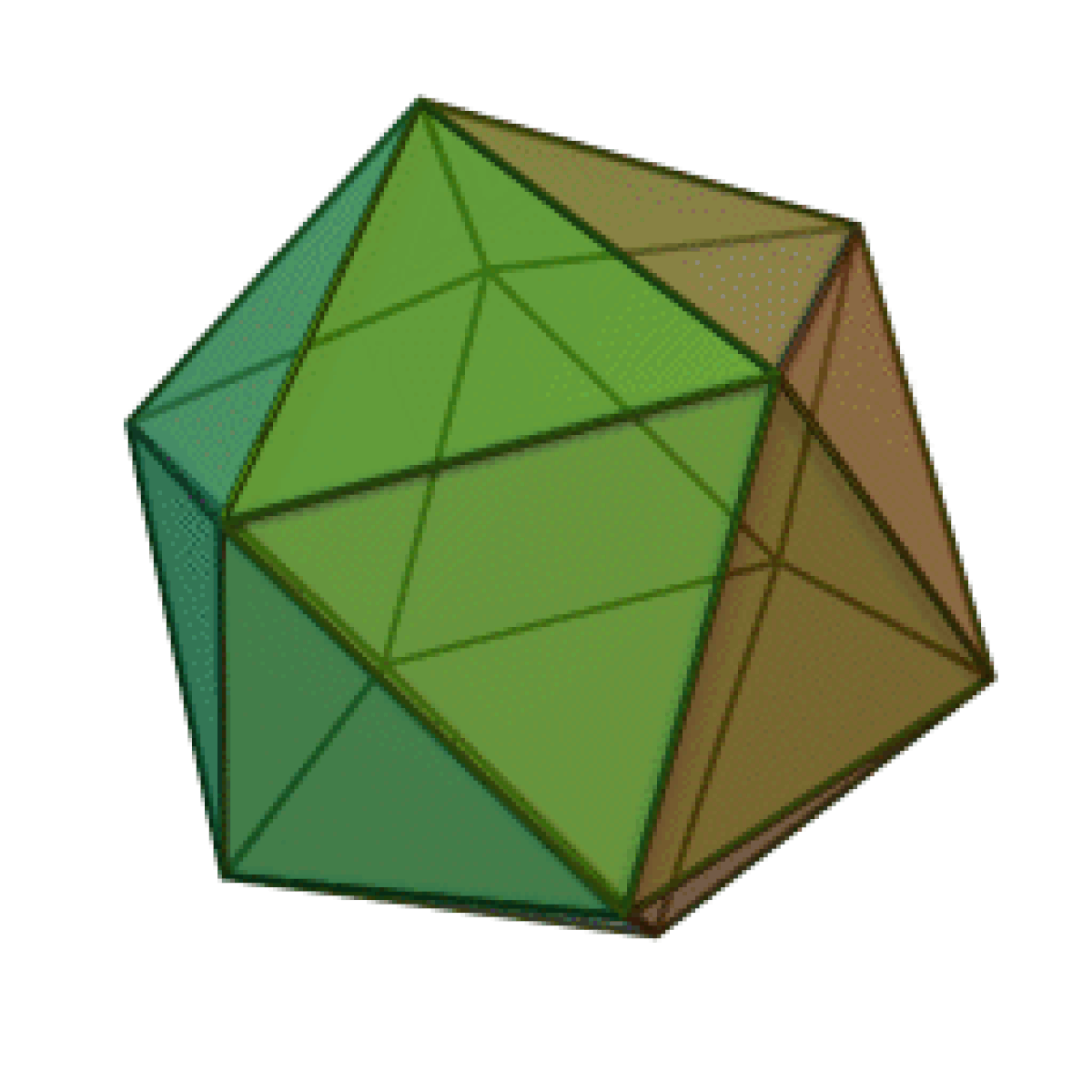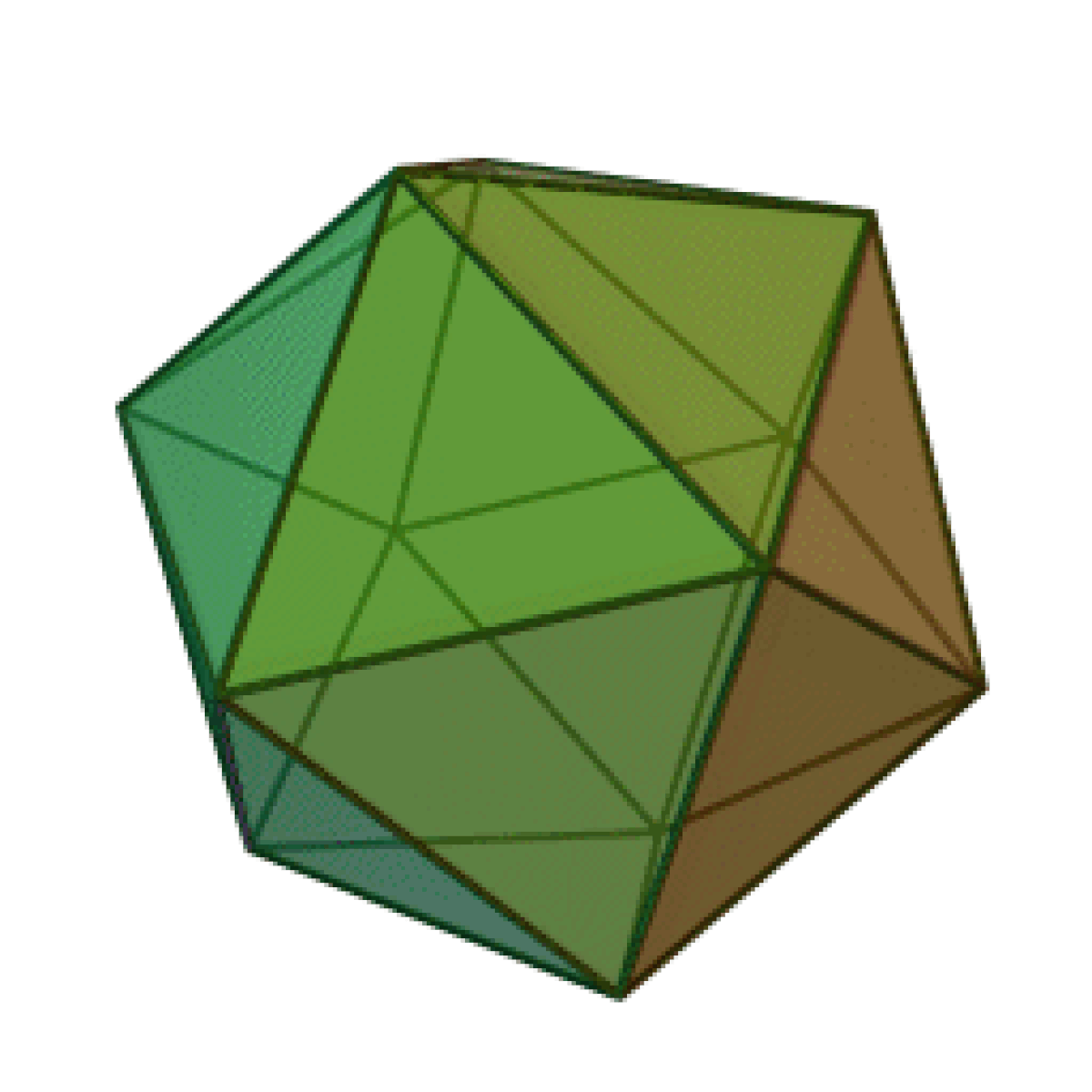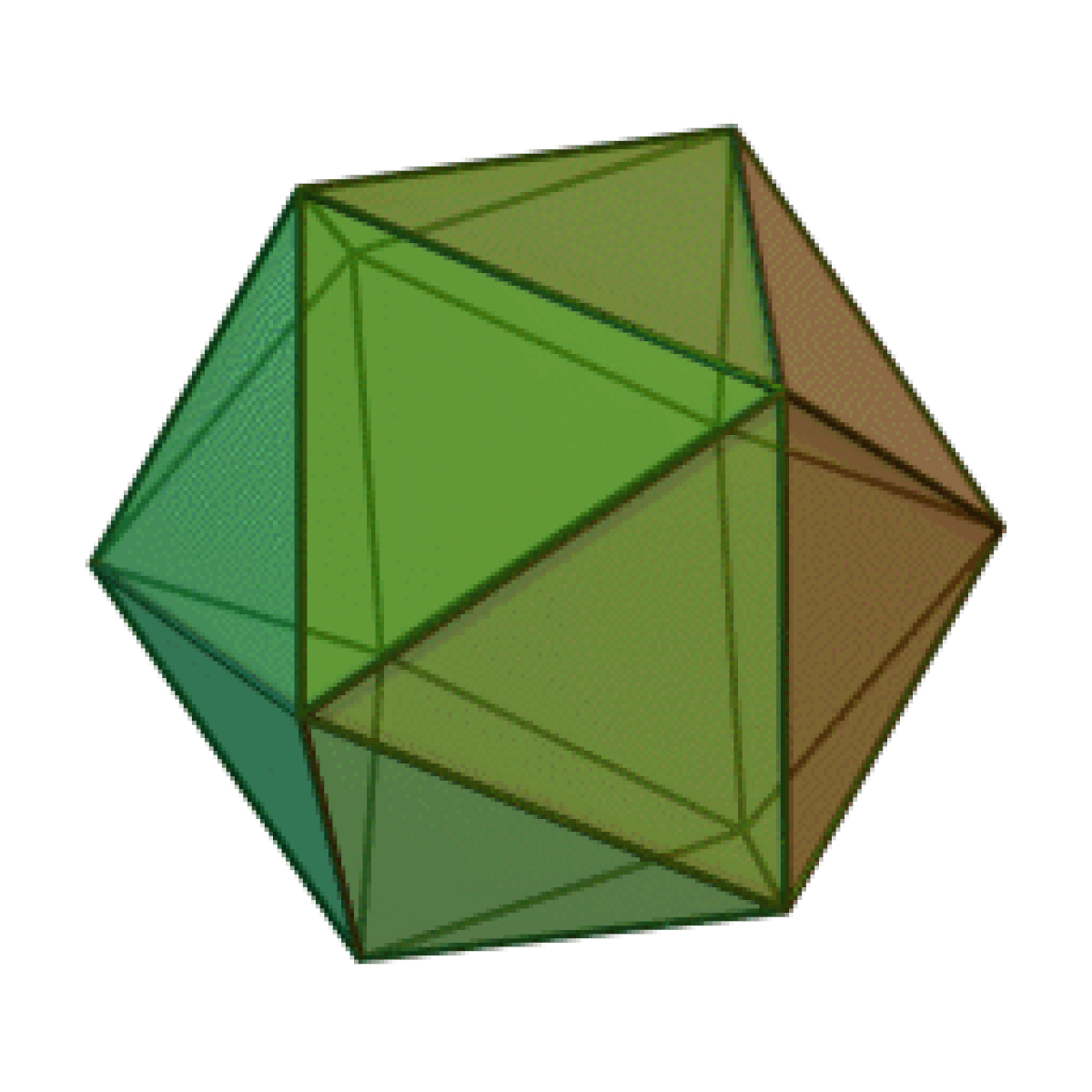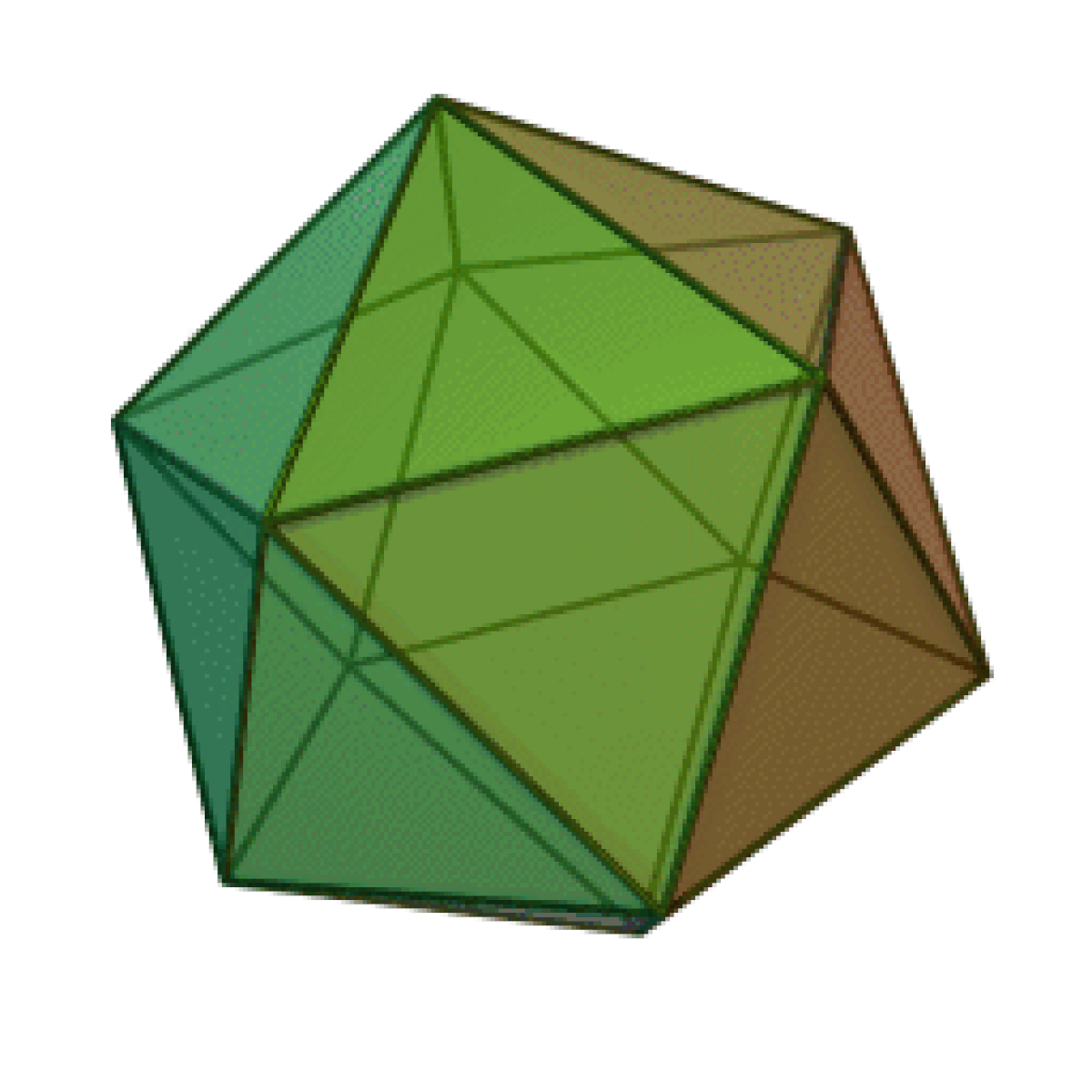
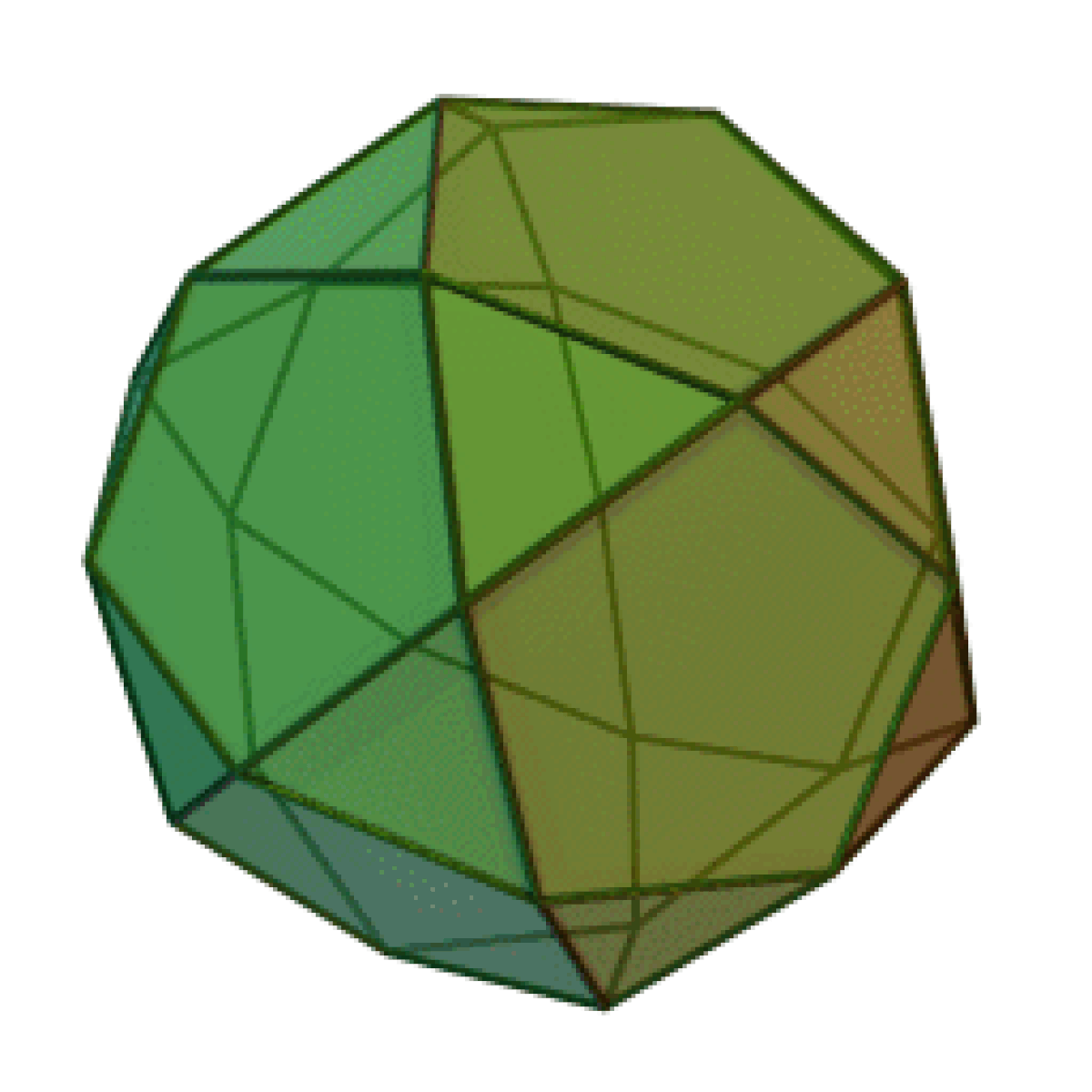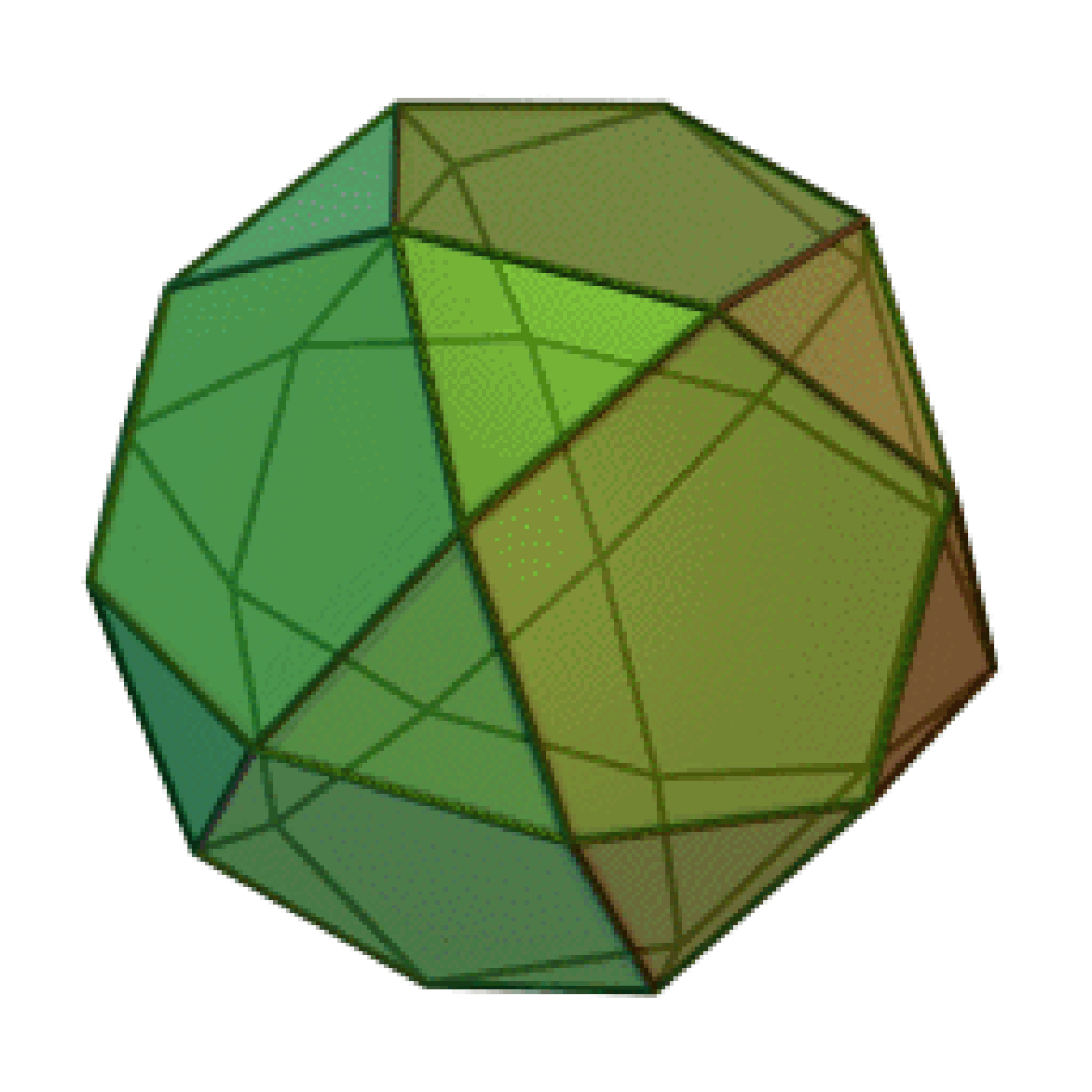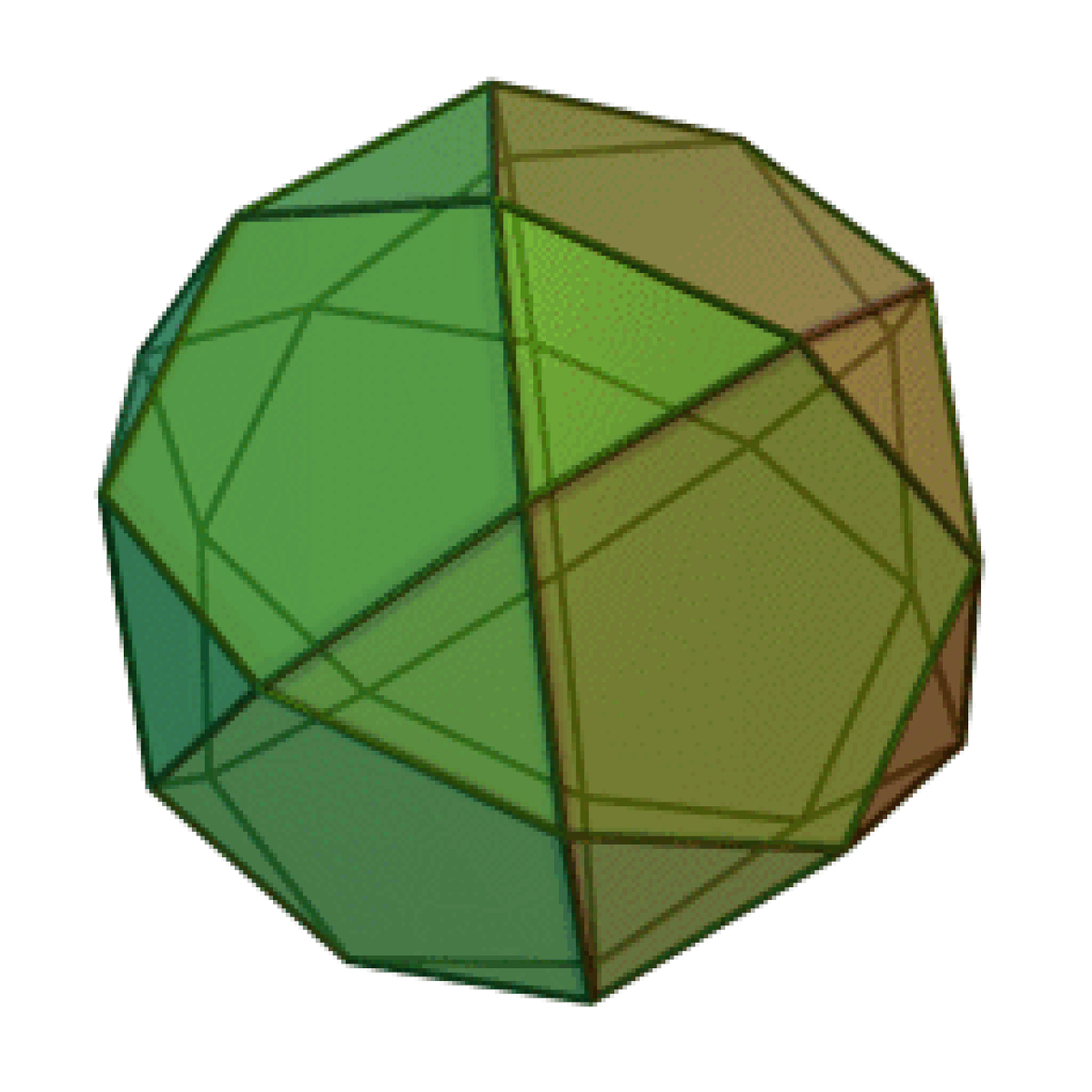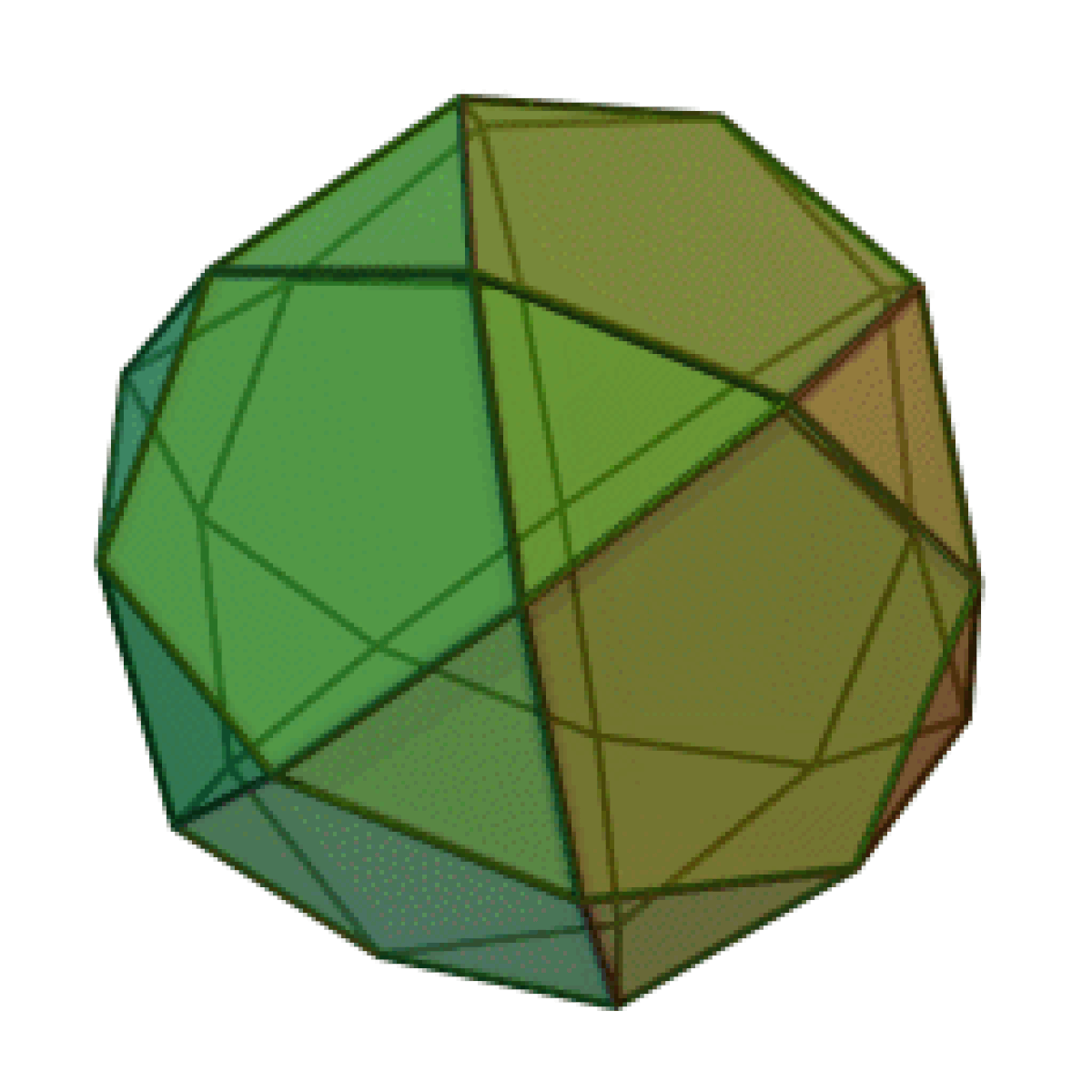
- L'octaèdre, qui est aussi un polyèdre régulier,
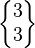
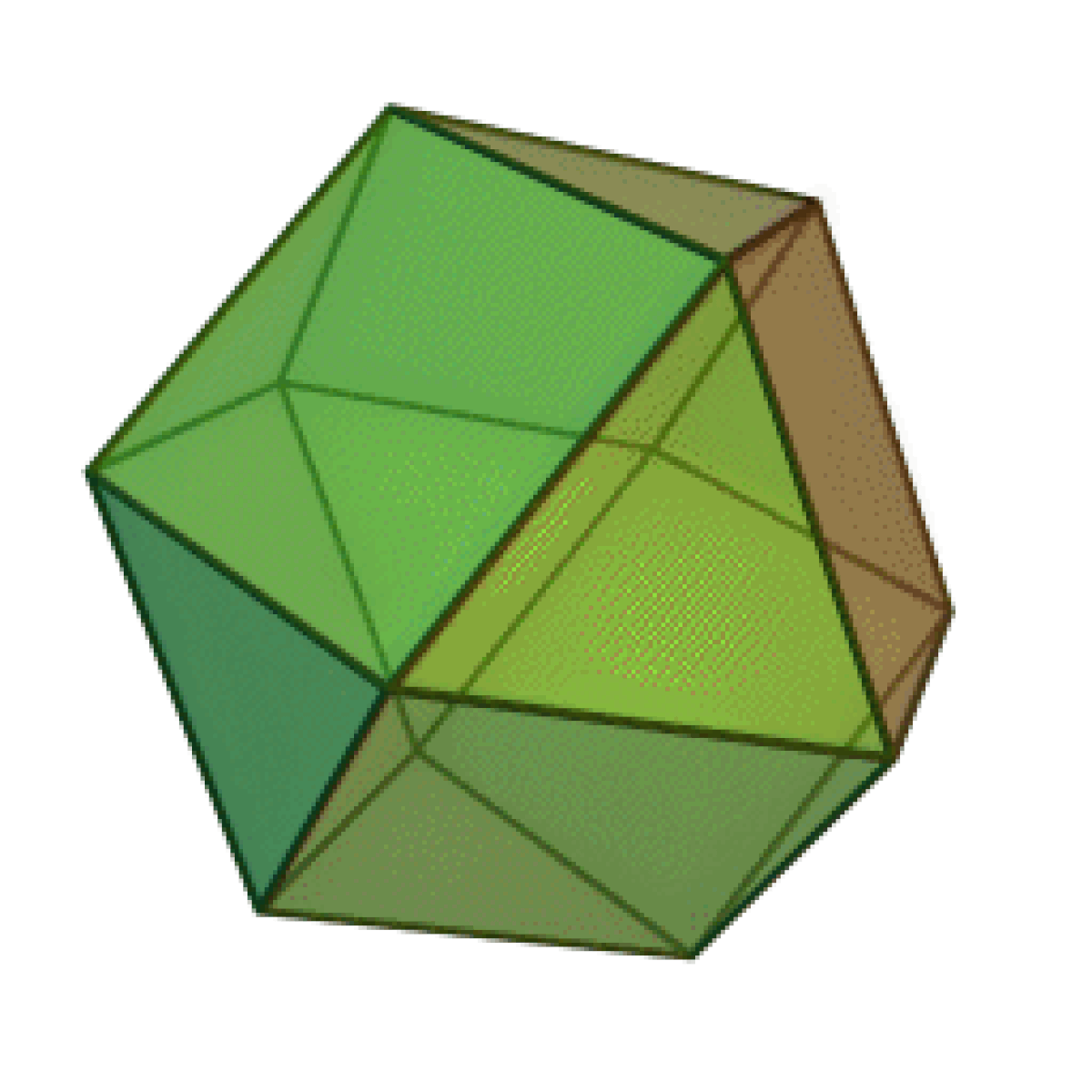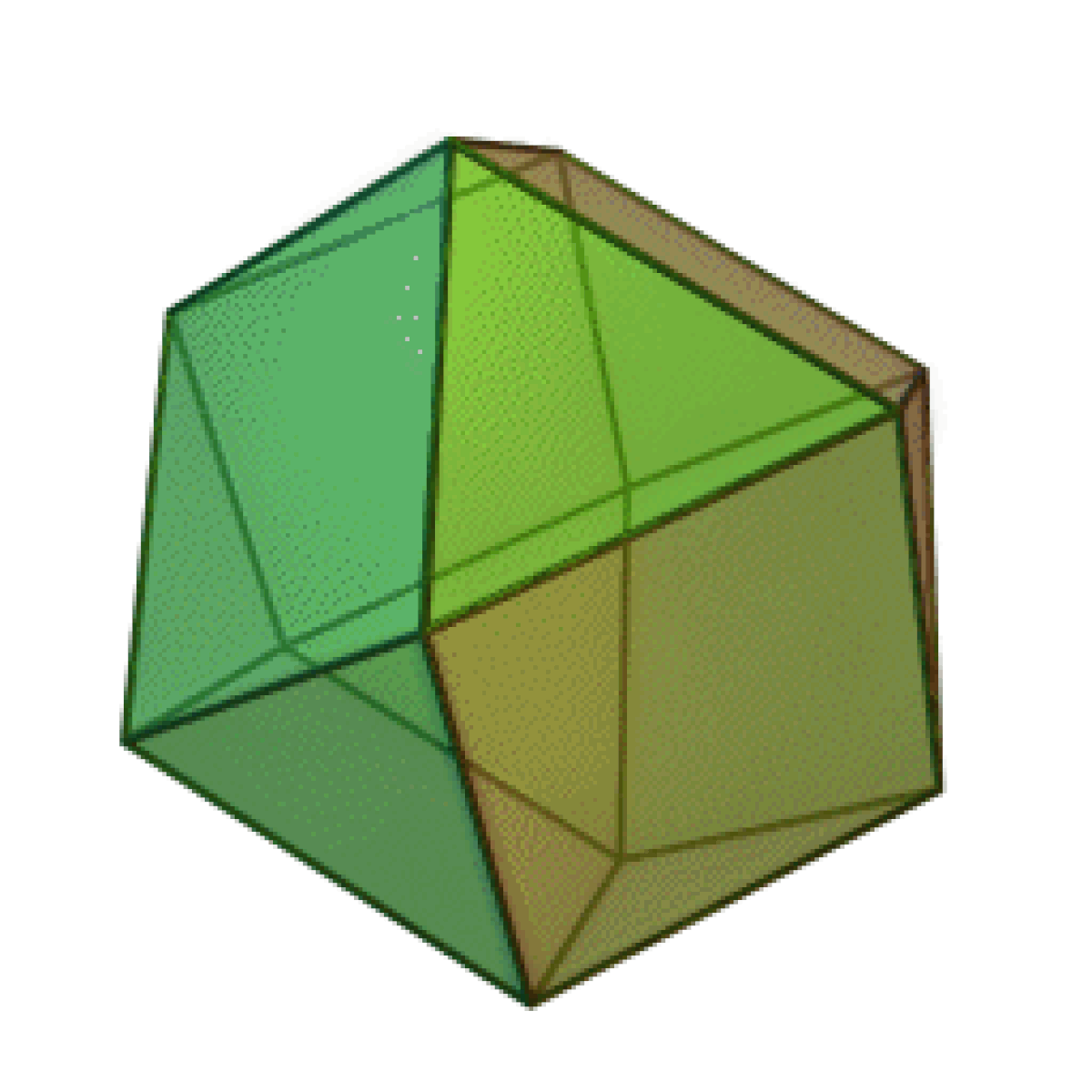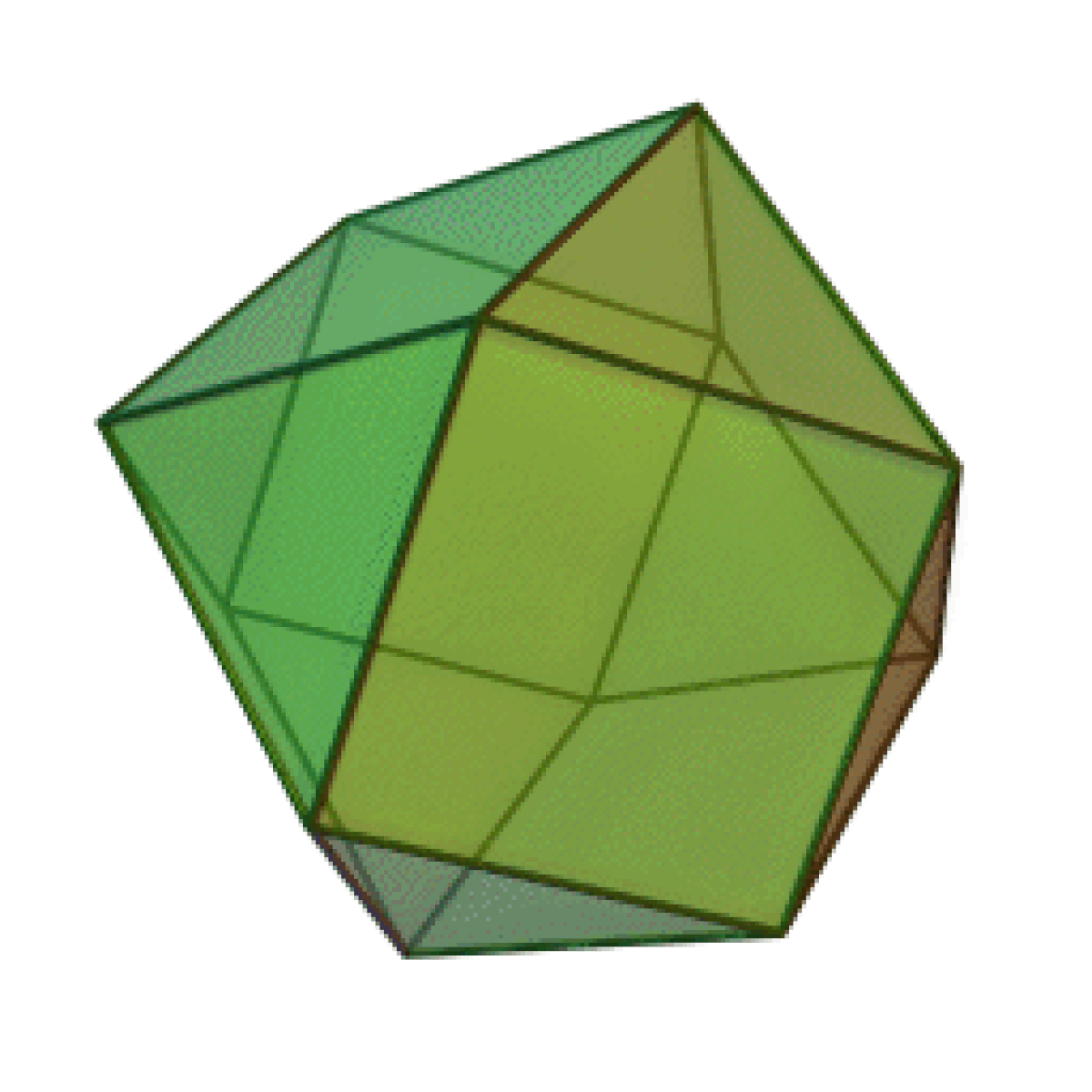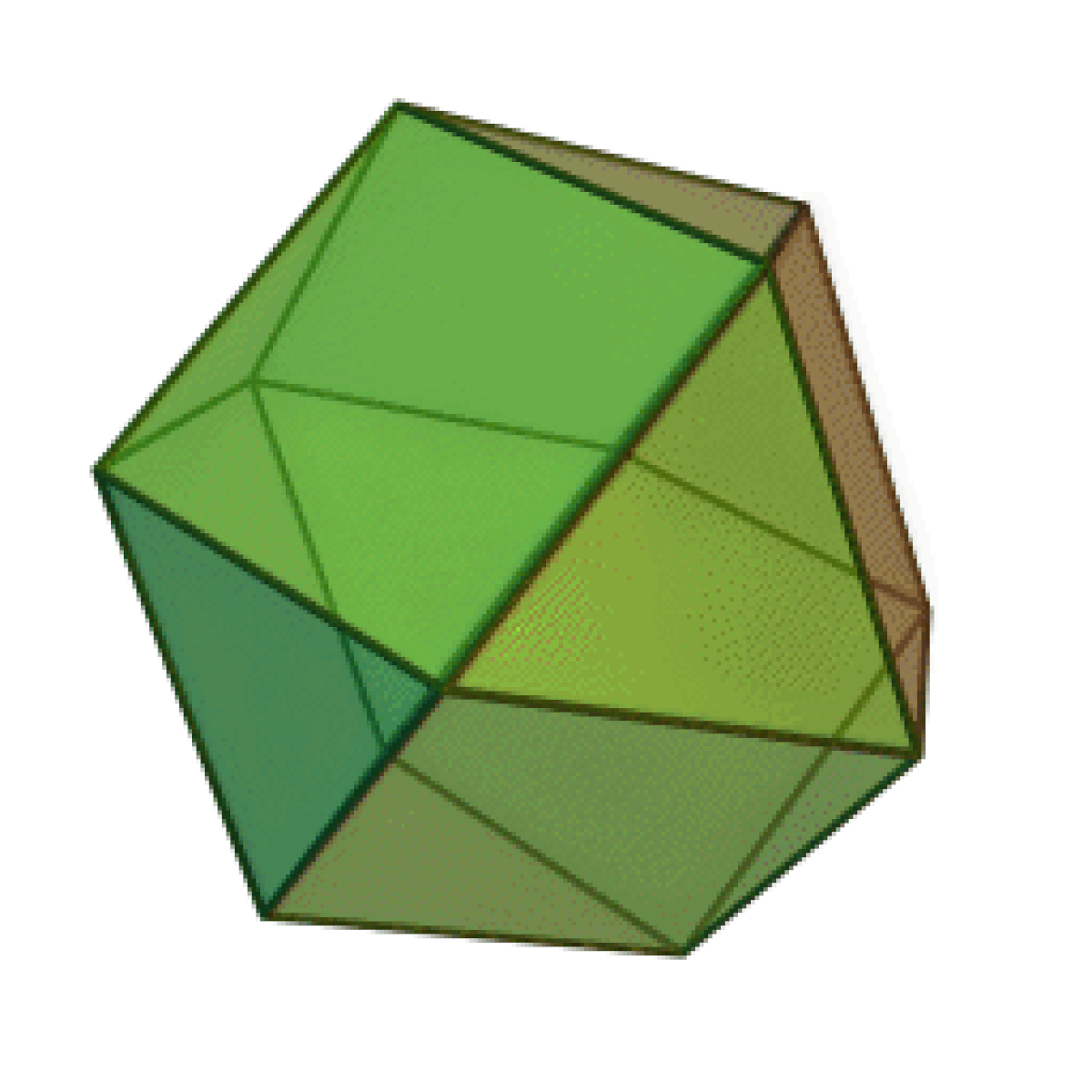
- Le cuboctaèdre
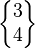
- L'icosidodécaèdre
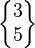
Chacun d'entre eux forme le noyau commun d'une paire duale de polyèdres réguliers. Les noms des deux derniers listés donnes des indices pour la paire duale associée, respectivement le cube + l'octaèdre et l'icosaèdre + le dodécaèdre. L'octaèdre est le noyau d'une paire duale de tétraèdres (un arrangement connu sous le nom octangle étoilé), et lorsqu'il est dérivé de cette manière, il est quelquefois appelé le tétratétraèdre.
Les duaux quasi-réguliers sont aussi caractérisés par leurs faces rhombiques.
Chacun de ces polyèdres quasi-réguliers peut être construit par une opération de rectification sur le parent régulier, en tronquant pleinement les arêtes, jusqu'à ce que les arêtes originales soient réduites à un point.
Duaux quasi-réguliers
Certaines autorités font remarquer que, puisque les duaux des solides quasi-réguliers partagent les mêmes symétries, ces duaux doivent être aussi quasi-réguliers. Mais tout le monde n'accepte pas ce point de vue. Ces duaux ont des sommets réguliers et sont transitifs sur leurs arêtes. Ils sont, en ordre correspondant avec ci-dessus :
- Le dodécaèdre rhombique
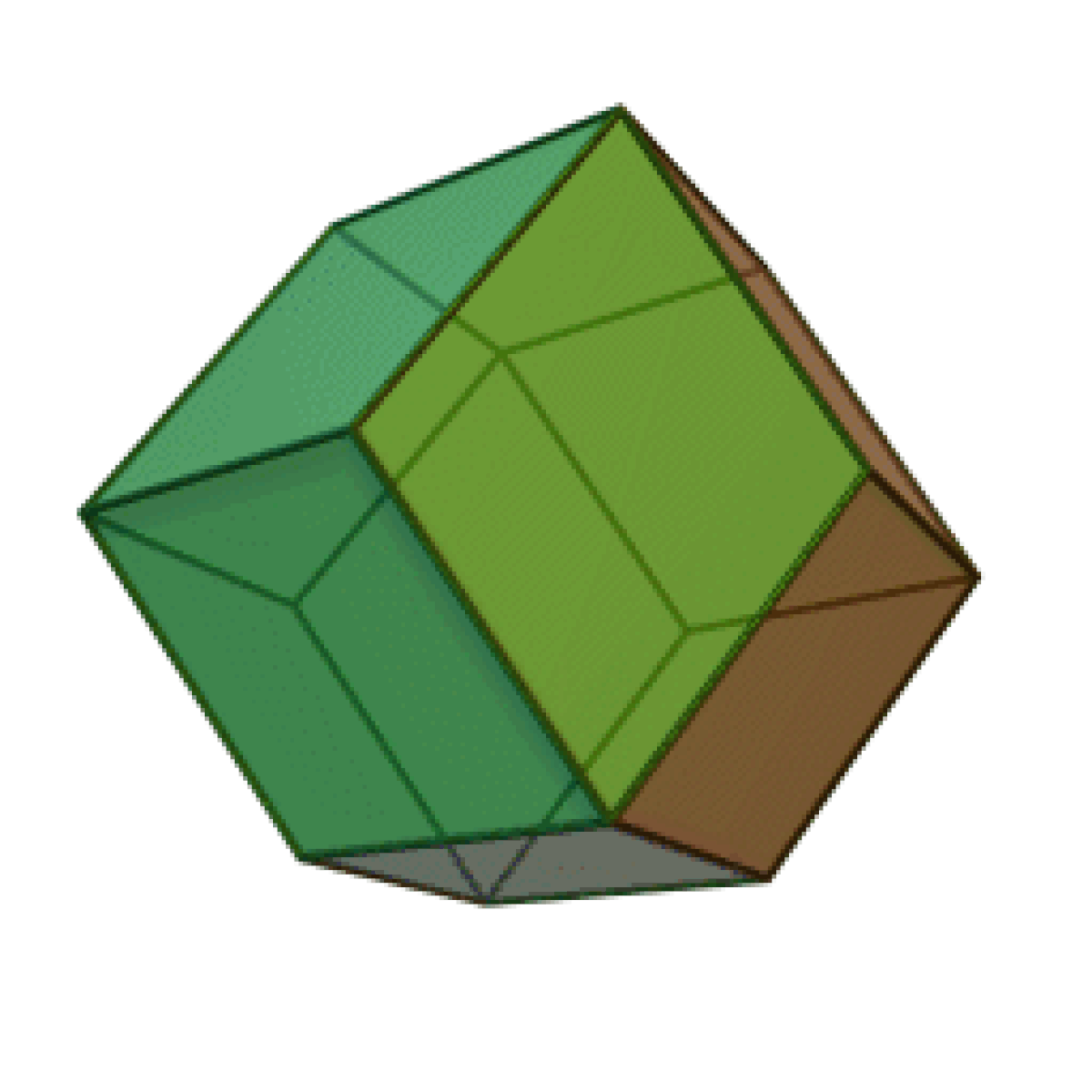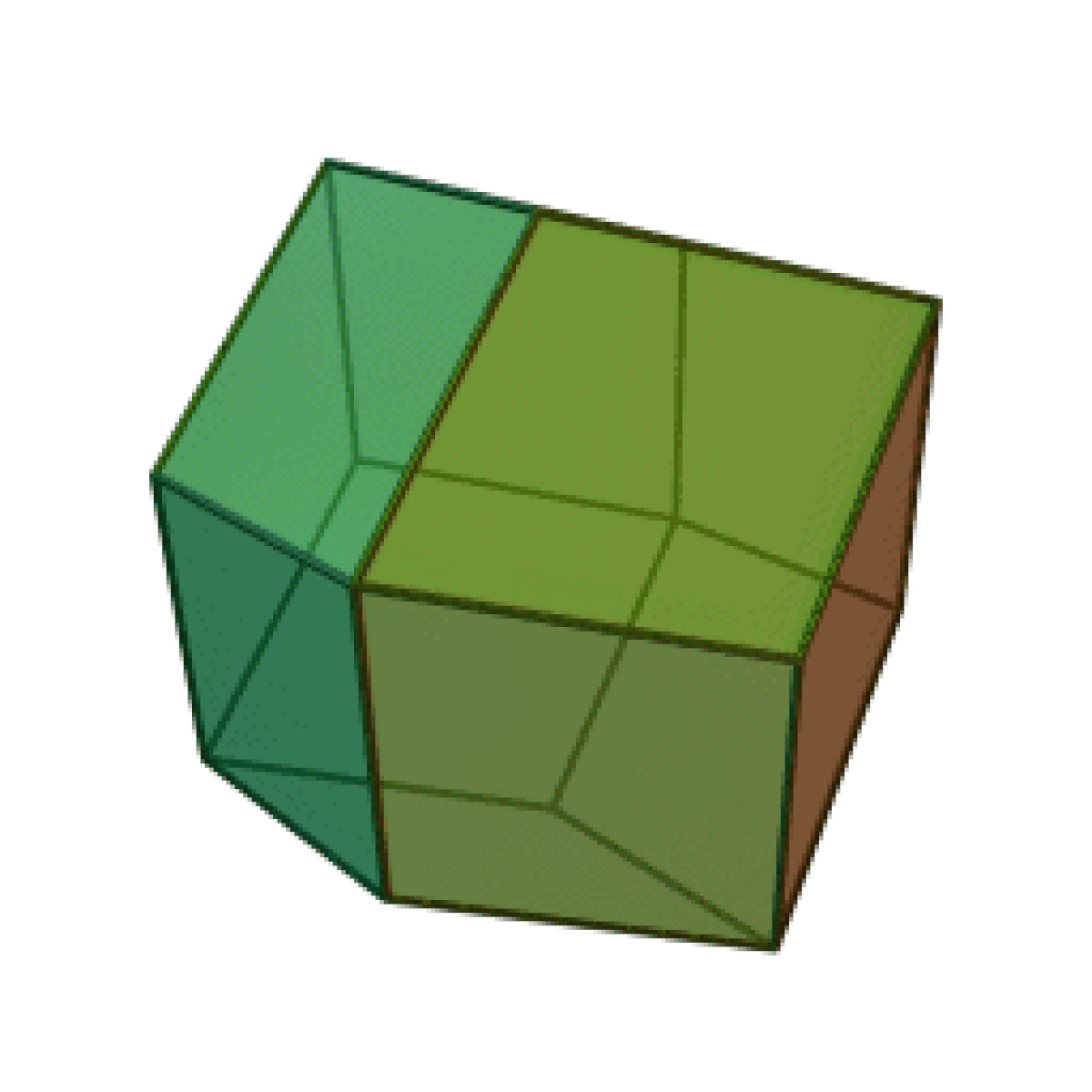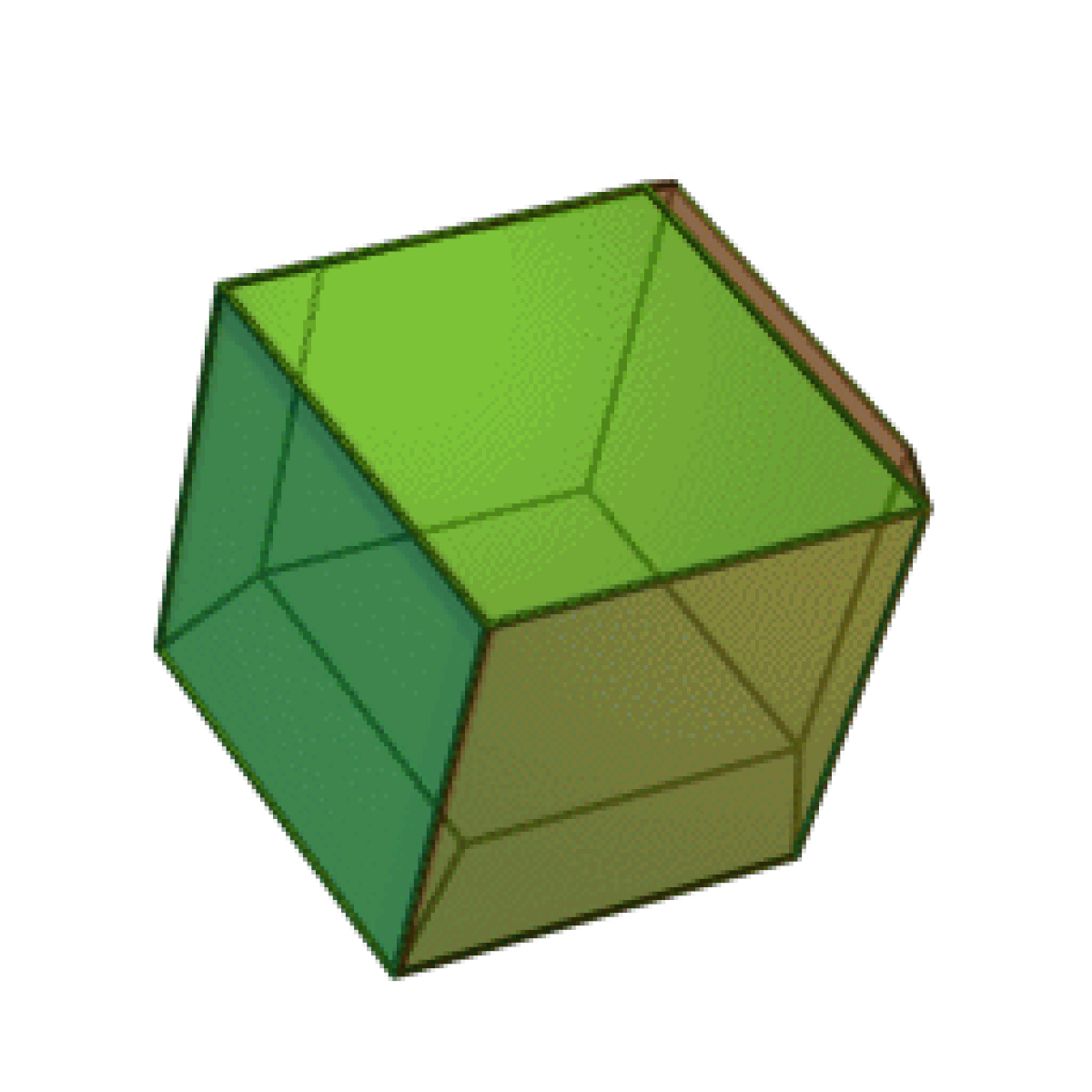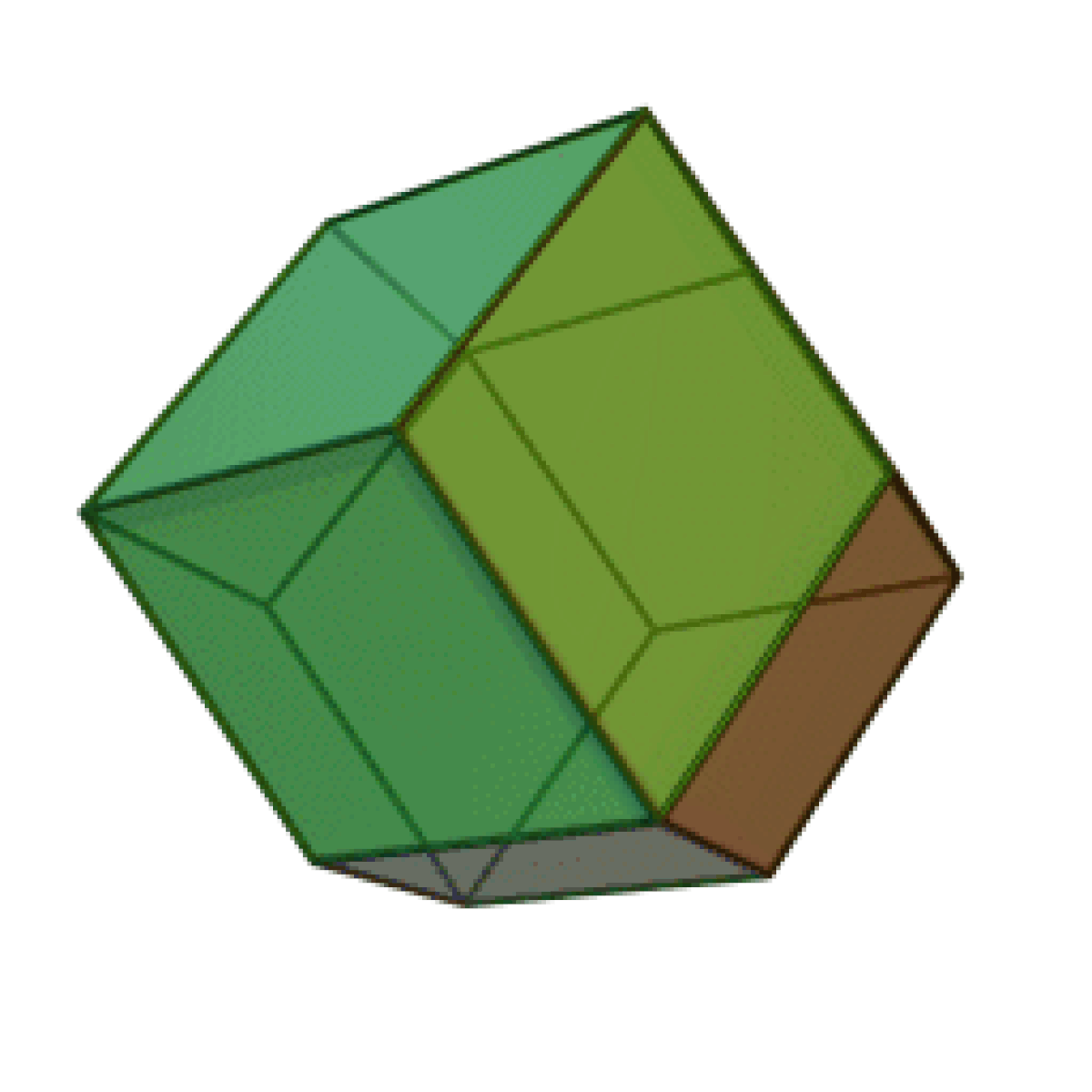
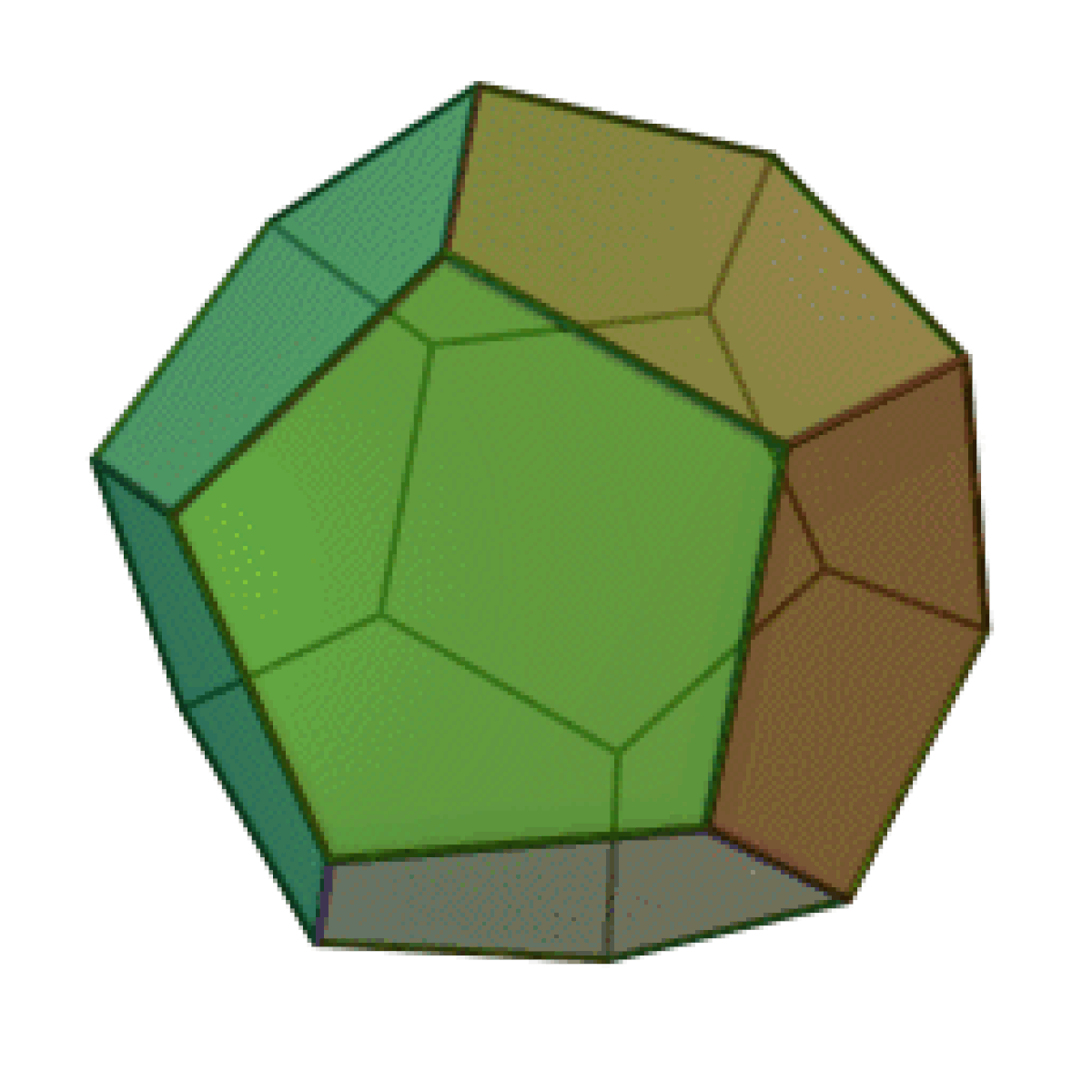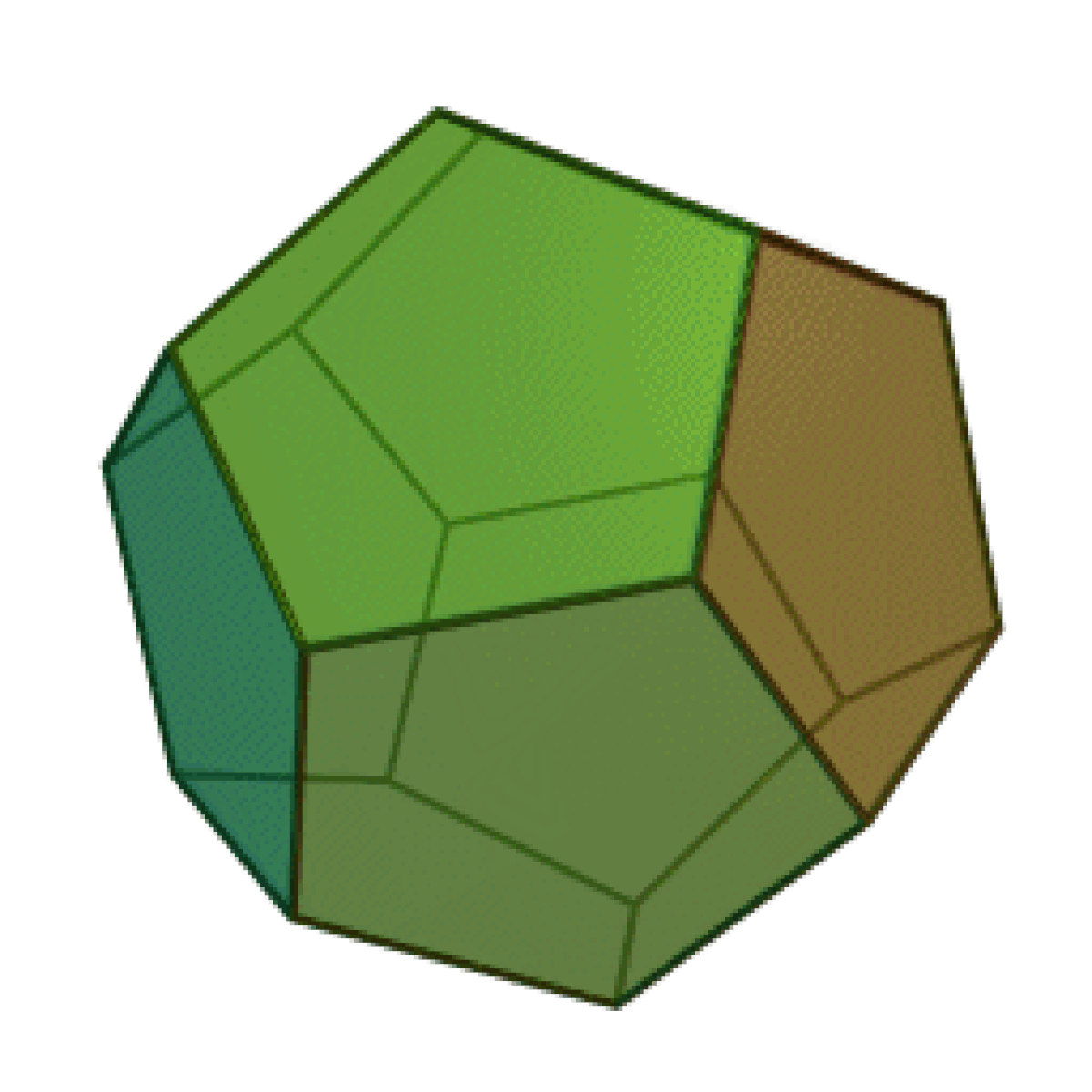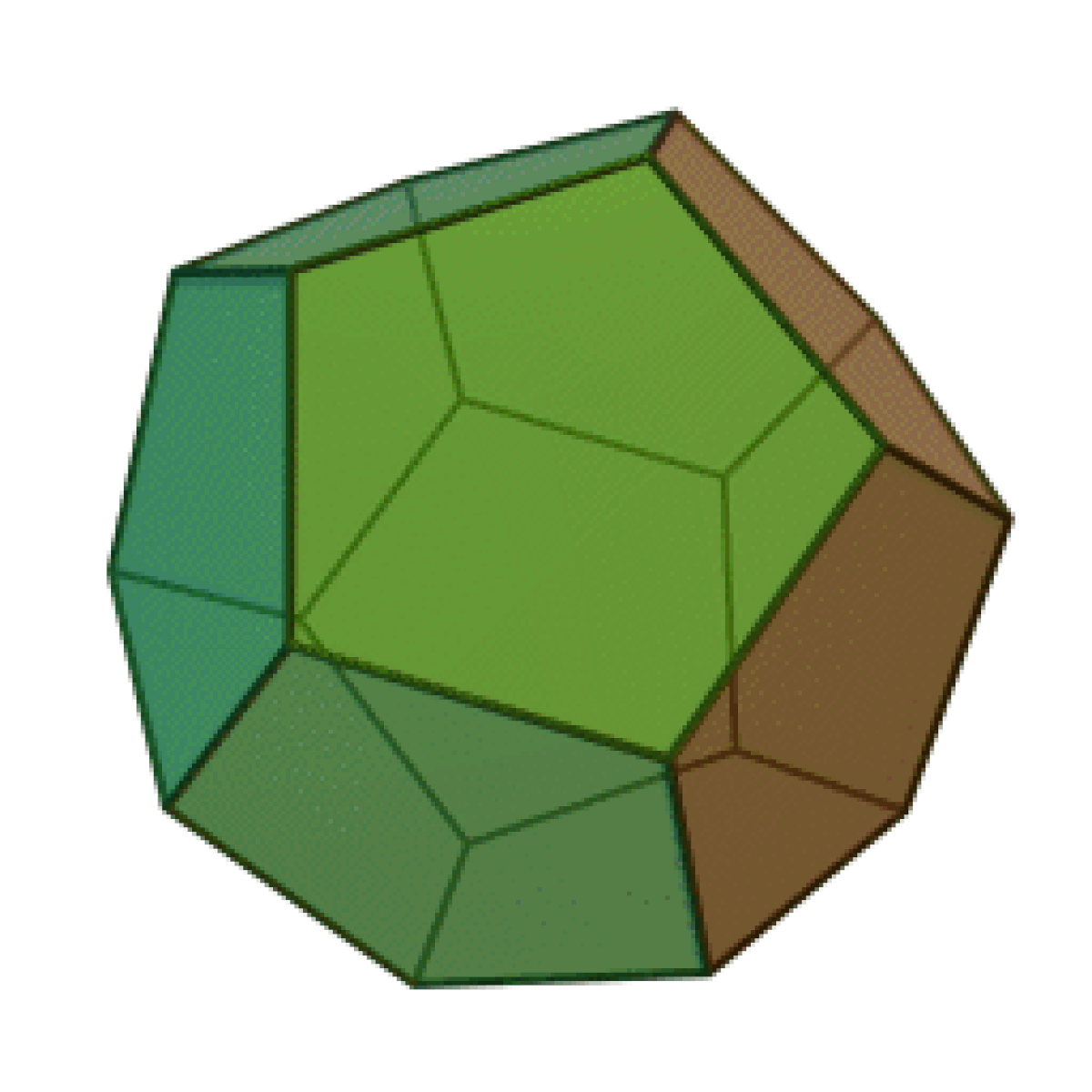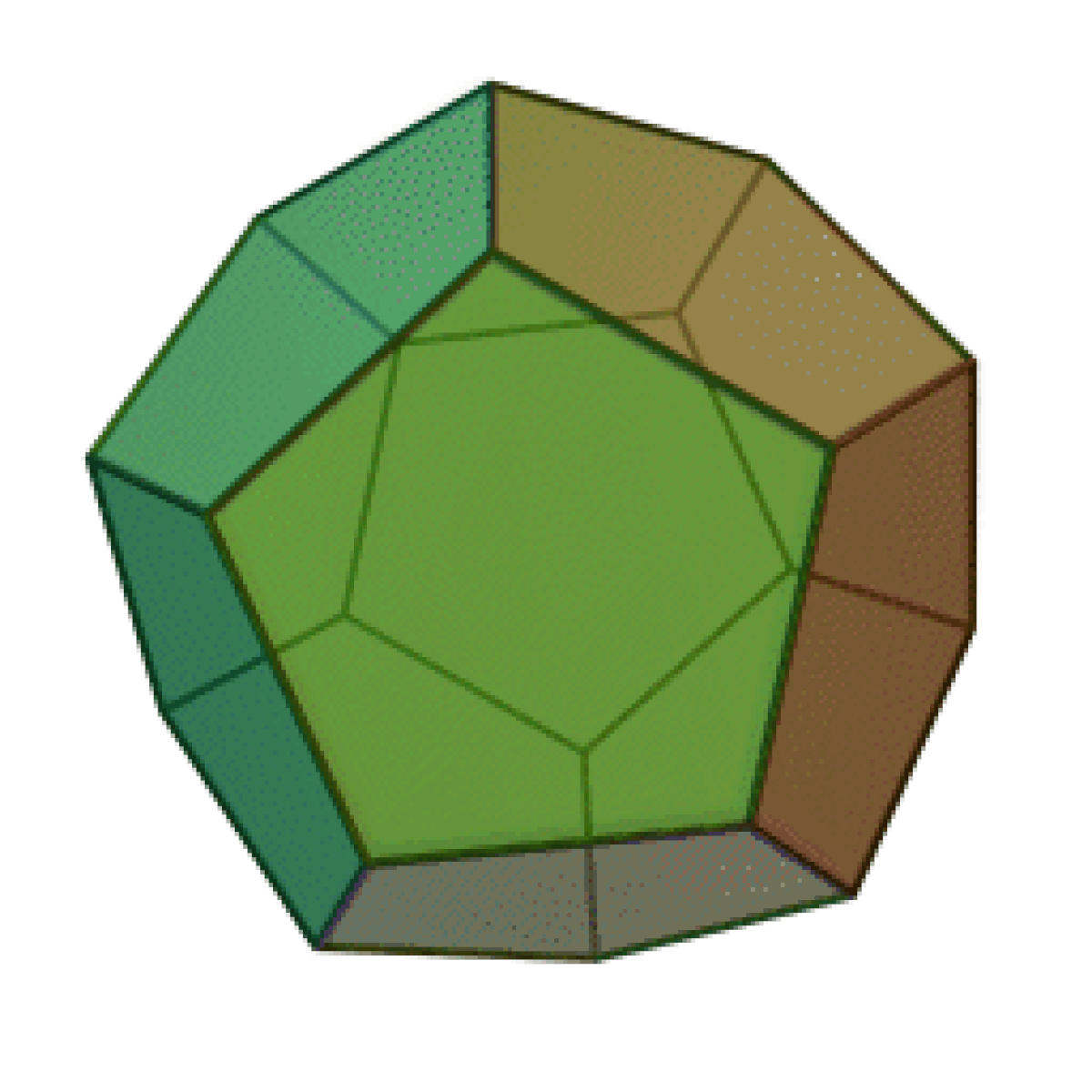
- Le triacontaèdre rhombique
- Le cube, qui est aussi un polyèdre régulier
Les duaux quasi-réguliers sont aussi caractérisés par leurs faces rhombiques.