Polymère en solution - Définition

Théorie de Flory-Krigbaum

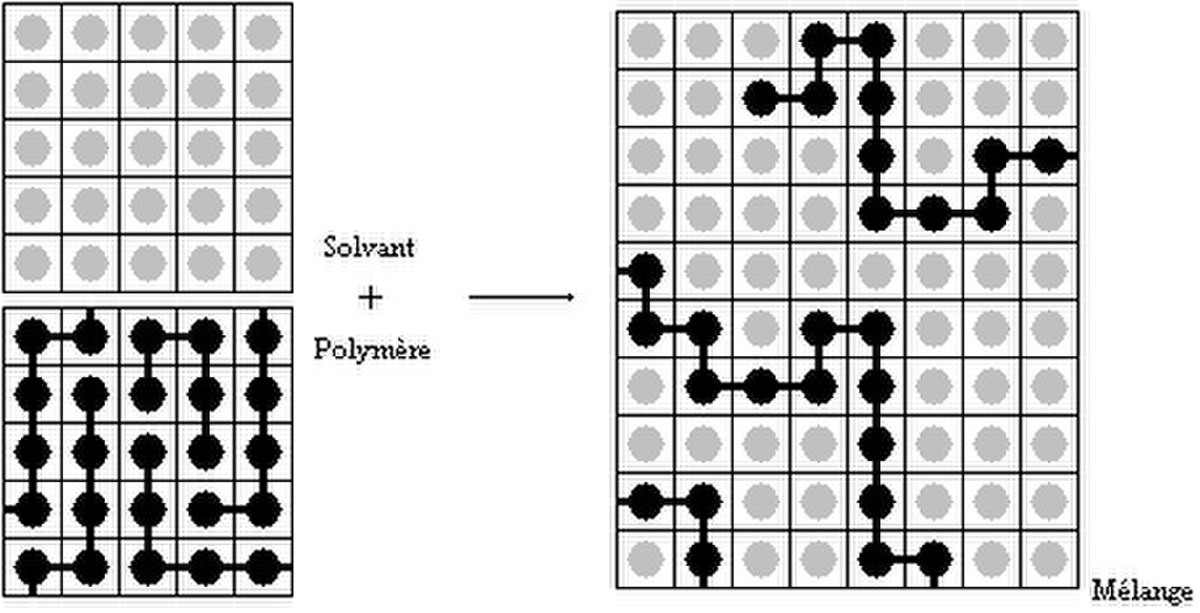
Cette théorie introduit la notion de volume exclu: il y a une répulsion entre chaînes, de nature géométrique, qui interdit la présence du centre de masse d'une autre chaîne de polymère autour d'une chaîne donnée.

Modélisation de la répartition des chaînes en tenant compte du volume exclu

Le paramètre de Flory calculé précédemment est modifié: . A un couple polymère solvant on peut associer une température θ et un paramètre ψ dit paramètre entropique, tous deux indépendants de la température: . Connaissant la température critique T_c (d'apparition du trouble) pour des échantillons d'un polymère de différentes masse molaire, on peut déterminer graphiquement la température θ et le paramètre entropique.

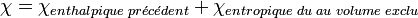
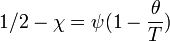
Le volume exclu (u), le paramètre de Flory et le second coefficient de Viriel du couple polymère/solvant A2 sont liés par les relations suivantes:
. Na est le nombre d'avogadro, N le nombre de segments, M la masse molaire, a le volume d'une unité monomère. Lorsque le paramètre de Flory est inférieur à 0.5, le volume exclu augmente: il y a extension des chaînes et on se situe en régime bon solvant. En mauvais solvant c'est l'inverse, il y a contraction des chaînes. On peut obtenir expérimentalement le volume exclu par osmométrie.

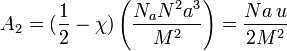
Analyse des polymères en solution

Il existe différentes techniques pour étudier les polymères en solution.

• méthodes thermodynamiques colligatives
  • osmométrie: accès à Mn, au deuxième coefficient de viriel A2
  • tonométrie
  • cryométrie et ébulliométrie
• méthodes viscosimétriques: accès à la viscosité, à la masse molaire moyenne viscosimétrique (Mn
• techniques hydrodynamiques: CES, accès aux masse molaire moyennes en masse et en mole
• techniques de diffusion de lumière
  • diffusion de lumière statique: accès à Rg, Mw, A2
  • diffusion de lumière dynamique: accès au rayon hydrodynamique et au coefficient de diffusion