Polymère en solution - Définition

Introduction

Comprendre le comportement des polymères en solution est important pour certaines applications comme les gels et crèmes cosmétiques. Il y a possibilité de contrôler la viscosité du produit obtenu et d'éviter une éventuelle démixtion (séparation de phase). On constate par exemple que le styrène est miscible en toute proportion dans le cyclohexane à 20 °C, mais que lorsqu'on polymérise le styrène, il n'y a plus miscibilité. Différentes théories peuvent expliquer ces phénomènes.

Théorie de Flory-Huggins

On modélise une chaîne de polymère par un ensemble de N maillons (unités monomères) de volume a. Le nombre moyen de chaînons est lié à au degré de polymérisation et à la masse molaire du polymère. Il est en solution dans un solvant avec une fraction volumique ou une concentration connue.

Mélange polymère solvant

On fait l'hypothèse que le volume molaire des unités monomères est égal à celui des molécules de solvant. Le mélange peut être représenté comme ceci:

Réseau de Flory-Huggins représentant le polymère en solution

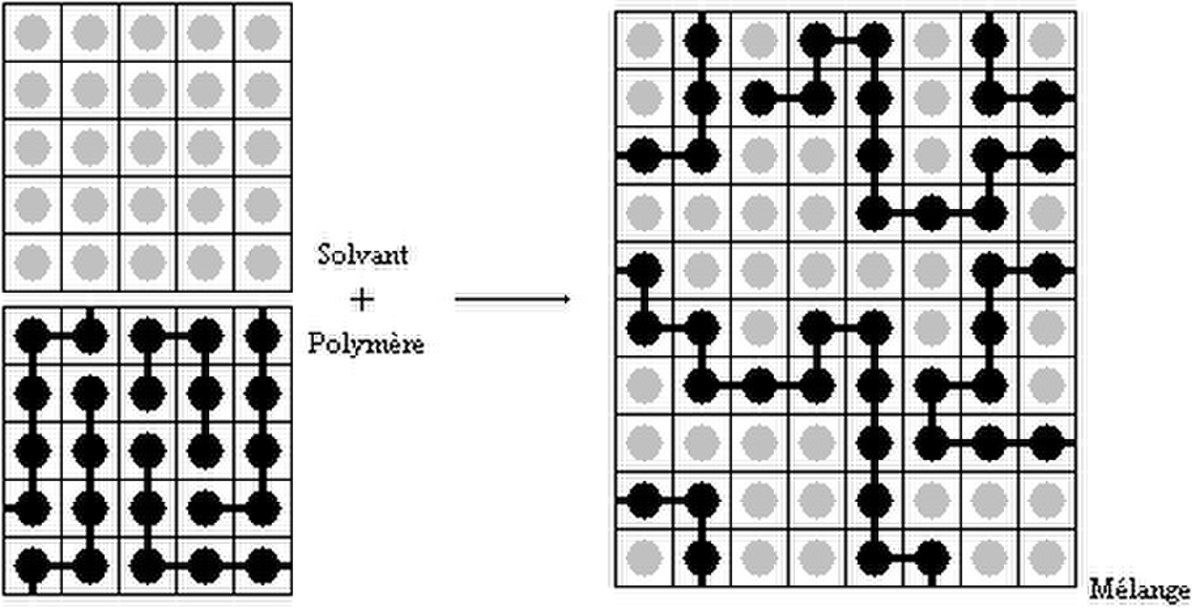
A température et pression fixées, l'enthalpie libre de mélange doit être négative pour que le mélange ait lieu. Dans le cas d'une solution régulière, des calculs de thermodynamique statistique permettent d'estimer cette enthalpie libre: avec k_B la constante de Boltzmann, T la température en kelvins, φ la fraction volumique et χ un paramètre sans dimension
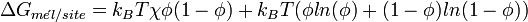
Pour un polymère dans un solvant, Flory a posé: avec N le nombre moyen d'unités monomère par chaîne.

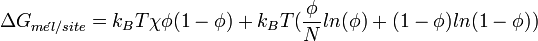
Cette enthalpie libre est en fait la somme de deux termes : est l'enthalpie de mélange et l'entropie de mélange, c'est cette dernière qui est diminuée par le facteur N. Quand N ou la masse molaire (c'est équivalent) augmente, l'entropie diminue, donc le désordre également. Il y a en effet moins de possibilités de répartir les unités monomères et les molécules de solvant sur la grille ci dessus quand les chaînes sont plus longues. Il en résulte une enthalpie libre de mélange plus difficilement négative quand le polymère a une plus forte masse molaire. Ceci est en accord avec la précipitation qu'on peut observer quand on synthétise un polymère en solution, donc dans un solvant.

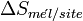
Paramètre de Flory

Le paramètre χ qui intervient dans l'expression de l'enthalpie et donc dans celle de l'enthalpie libre, permet de tenir compte des interactions entre le polymère et le solvant. Dans ce modèle, où Z est le nombre de premiers voisins des unités monomères ou des molécules de solvant, l'énergie d'interaction entre unité monomère et solvant, l'énergie d'interaction entre unités monomères, et l'énergie d'interaction entre molécules de solvant.
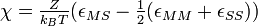
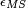
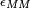
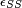
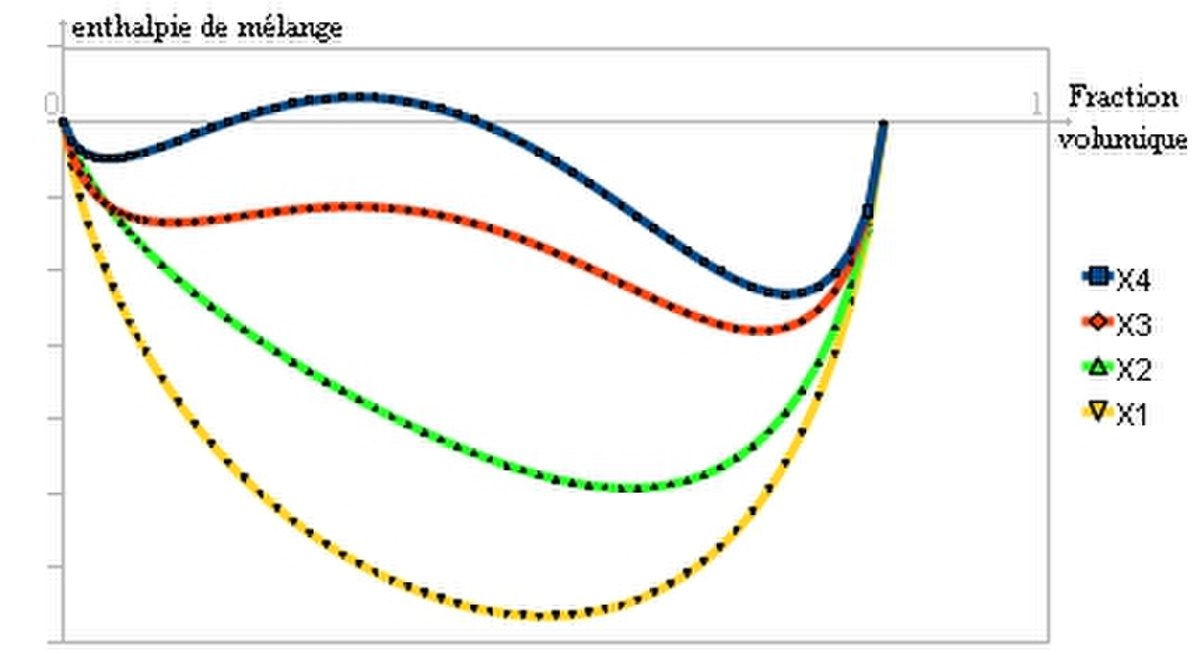
Il s'agit du paramètre de Flory, qui joue un rôle important dans l'évolution de l'enthalpie libre:

Lorsque le paramètre de Flory augmente: χ₁ < χ_c < χ₂ < χ₃ < χ₄ , une zone de démixtion apparait et a lieue sur une plage de fractions volumiques de plus en plus grande.

A partir d'une certaine valeur de χ, la courbe présente deux points d'inflexion et il est possible de tracer une double tangente. C'est le signe d'une séparation en deux phases comme ceci:

Il y a démixtion entre une phase riche en polymère et une phase pauvre, de fraction volumique en polymère φ_R et φ_P respectivement

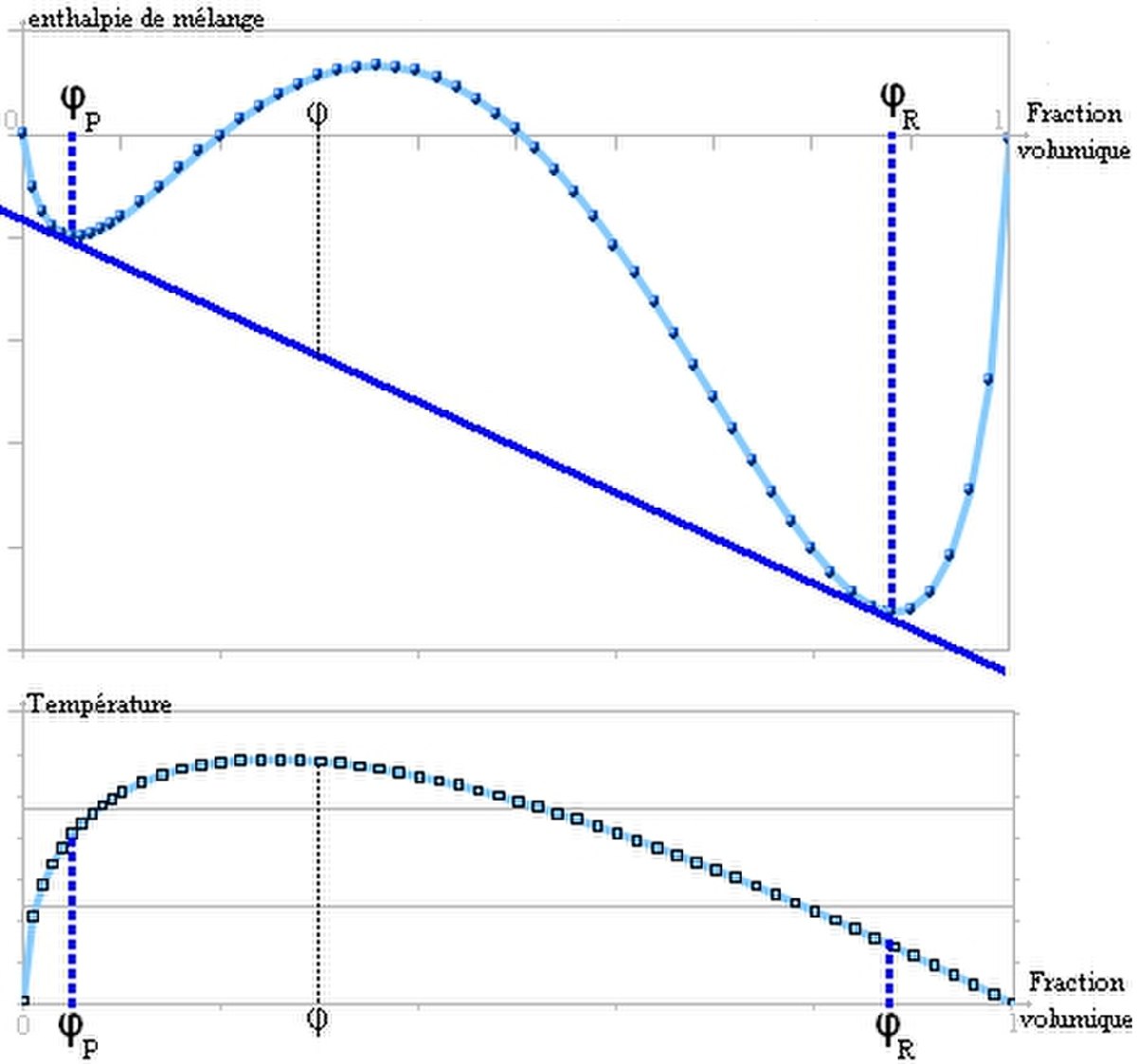
On peut calculer cette valeur critique de paramètre de Flory, notée et obtenue pour .

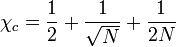
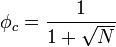
Pour résumer, la démixtion apparait quand le paramètre de Flory dépasse une valeur critique qui dépend de la masse molaire. Ceci peut se comprendre également en comparant les interactions qui apparaissent dans l'expression de ce paramètre. Lorsque χ est grand, domine. Cette énergie attractive est bien sur négative et lorsqu'elle est grande, elle diminue en valeur absolue: l'attraction entre polymère et solvant faiblit. Les maillons des chaînes de polymère sont attirés entre eux et le polymère sera de moins en moins solubilisé.

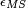
On peut accéder à ce paramètre de Flory expérimentalement par des mesures de pression osmotique par exemple.

Diagramme d'état φ-T

Pour un système polymère/solvant, si les interactions de VdW de type London dominent (typiquement en milieu apolaire), on peut montrer que χ varie comme l'inverse de la température. A basse température le paramètre de Flory sera grand et on aura une démixtion, et inversement.

Par contre lorsque les liaisons H dominent (milieu polaire), χ augmente avec la température et on a donc la situation inverse. A haute température l'agitation thermique rompt les liaisons H qui liaient polymère au solvant et la séparation de phase à lieue.

Pour obtenir ces diagrammes de phase, on peut partir de tubes contenant différentes fractions molaires en polymère et observer à quel moment chaque tube devient trouble lorsqu'on les refroidis à partir d'une température pour laquelle on a mélange. Le trouble est du à la diffusion de la lumière dans toutes les directions par les particules qui apparaissent quand la séparation de phase à lieue:

Apparition du trouble du aux gouttelettes qui diffusent la lumière