Polymère en solution - Définition

Pression osmotique et qualité de solvant

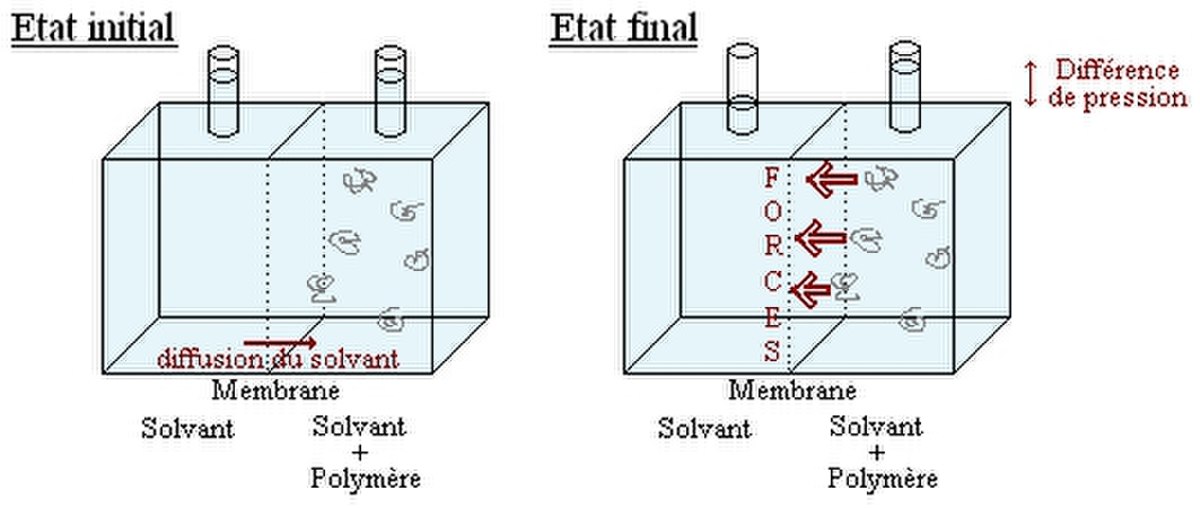
Soient deux compartiments séparés par une membrane semi perméable:

Illustration de la pression osmotique

Le compartiment de droite contient le polymère en solution dans un solvant, tandis que le compartiment de gauche ne contient que le solvant. On observe une variation de la pression entre les 2 compartiments. Plus précisément les chaînes de polymère exercent une force sur la paroi. Cette force par unité de surface est appelée pression osmotique. On peut la calculer moyennant quelques hypothèses à partir de l'enthalpie de mélange vu précédemment.
Si la fraction volumique en polymère n'est pas trop grande, on obtient:

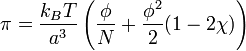
On se rend compte que la valeur du paramètre de Flory joue ici encore un rôle:

• s'il est supérieur à 1/2, la pression osmotique diminue, cela revient à dire qu'il y a moins de chocs de particules sur la paroi et qu'elles ont plutôt tendance à rester entre elles. le polymère est plus difficile à dissoudre, on est en régime mauvaise solvant. Le polymère peut cependant être dissous ou avoir précipité: χ_C > 1 / 2.
• s'il est inférieur à 1/2, la pression osmotique augmente et c'est l'inverse: le solvant dissous bien le polymère et on dit dit qu'on est en régime bon solvant. Si le polymère est sous forme de pelotes, cela se traduira par un gonflement de ces dernières. Le monomère est souvent un bon solvant pour son polymère, comme par exemple le styrène pour le polystyrène.
• la valeur limite χ = 1 / 2 correspond à ce qu'on appelle solvant θ (théta), auquel correspond une température θ. La température critique Tc vue plus haut tend vers cette température θ lorsque la masse molaire tend vers l'infini, ce qui permet d'accéder à θ par extrapolation.

Le paramètre de Flory χ varie avec la température. Lorsqu'il prend la valeur limite 1/2, la température associée porte le nom de température théta. Cette température particulière peut souvent se trouver dans des tables pour un couple polymère/solvant. Par exemple le cyclohexane est un solvant théta du polystyrène à 307,2 K.

Approche de Hildebrand, paramètre de solubilité

On définit l'énergie de cohésion du système et la densité d'énergie cohésive qui s'obtient en divisant la première par le volume molaire: . Le paramètre de solubilité est alors égal à la racine carrée de cette densité c: . Les valeurs de paramètre de solubilité sont tabulées pour de nombreux solvants et de nombreux polymères. on peut montrer que le paramètre de Flory vu précédemment peut s'écrire:

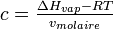
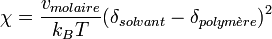
Si on cherche un bon solvant pour un polymère donné il faut donc chercher un paramètre de solubilité qui soit proche de celui du polymère, pour minimiser le paramètre de Flory. On peut ainsi éliminer bon nombre de solvants pour un polymère donné, mais même si les paramètres de Hildebrand sont proches la solubilité n'est pas assurée.

On peut aussi calculer le paramètre de solubilité comme ceci: où G(i) est la constante d'attraction molaire du groupe i.

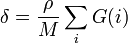
Régimes de concentration et loi d'échelle

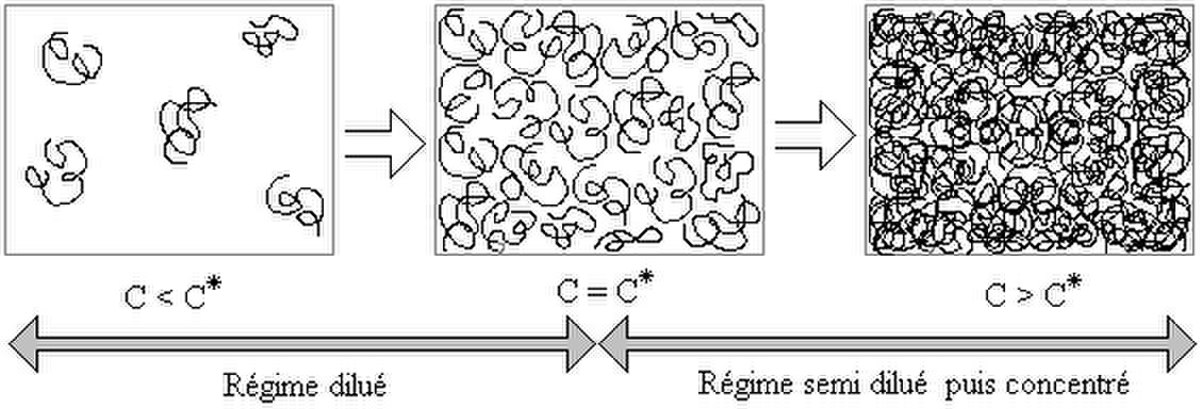
Il existe différents régimes, selon la concentration et la masse du polymère en solution. Pour des raisons entropiques, les chaînes de polymère ne sont pas dépliées mais elles se contractent sur elle même pour former des pelotes.

Du régime dilué au régime semi dilué

Soient des pelotes de polymère en solution. Lorsqu'on augmente la concentration (ou la fraction volumique ce qui revient au même), la distance entre pelotes diminue. A partir d'un moment, il y a contact entre ces dernières et on appelle concentration critique de recouvrement la concentration associée. Elle marque la transition entre le régime dilué et le régime semi dilué. Il est encore possible d'augmenter la concentration dans le régime semi dilué, car la fraction de polymère contenue dans une pelote est vraiment faible.

Effet d'une augmentation de la concentration sur les pelotes de polymère en solution

On peut calculer la concentration critique de recouvrement à l'aide de la relation suivante: .
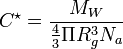
La fraction volumique dépend du nombre de segments des chaînes à la puissance -4/5.

Rayon de giration en régime dilué

Cette distance a une influence sur les propriétés physicochimiques du système. En bon solvant, , avec Rg le rayon de giration des pelotes, N le nombre de segments de la chaîne qui constitue la pelote et a la taille de ces segments. En solvant θ, . On peut comprendre cette différence d'exposant en prenant en compte le fait qu'en bon solvant χ < 1 / 2, les interactions répulsives entre segments de pelotes dominent. Les pelotes gonflent et leur rayon de giration augmente.

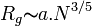
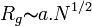
En solvant θ, il existe différents modèles pour calculer le rayon de giration:

• modèle de la marche au hasard: < R_g > ² = N.a²
• rotation libre: où θ est l'angle de valence, pris selon cette convention:

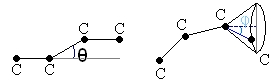
• rotation gênée: on tient compte des interactions entre groupements moléculaires. . φ est l'angle de rotation interne ou angle dièdre. On peut voir cos(φ) comme un coefficient de rigidité.

Si on n'est plus en conditions θ, on peut introduire un coefficient d'expansion volumique comme ceci: .

Grandeur caractéristique en régime semi dilué

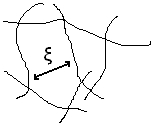
Lorsque les pelotes s'interpénètrent, on ne peut plus vraiment parler de rayon de giration, vu qu'on ne peut pas distinguer les pelotes. On définit la distance moyenne entre points d'enchevêtrement, notée ξ. Cette grandeur est égale à R_g lorsqu'on est à la concentration critique de recouvrement. Elle diminue ensuite lorsque la concentration augmente. Les propriétés du système dépendent de cette grandeur dans le régime semi diluée. On peut montrer que: en bon solvant.

ξ est une longueur de corrélation, ou maille de réseau.

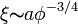
Le régime enchevêtré

Il est possible quand la masse dépasse une masse critique d'enchevêtrement Mc. Il peut apparaître dans le régime semi dilué, voir dans le régime concentré (quand on augmente encore plus la concentration). Dans le régime enchevêtré, le mouvement des chaînes est est très gêné par celui des autres chaînes. Son mouvement est décrit par le modèle de reptation. La viscosité dépend alors de la concentration à la puissance 3.75 et de la masse au cube. En régime non enchevêtré, la viscosité dépend de la concentration à la puissance 2.5 seulement et les chaînes ont une dynamique dite de Rouse. Cette effet plus ou moins grand de la concentration permet de jouer sur la viscosité du système de manière importante et peut être utilisé lors de la confection de gels de polymère.