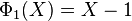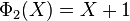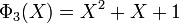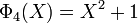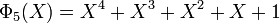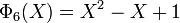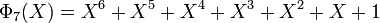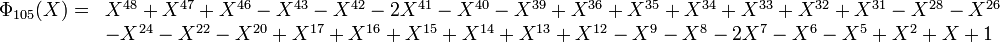Polynôme cyclotomique - Définition
La liste des auteurs de cet article est disponible ici.
Définition et exemples
Définition
-
- Soit n un entier strictement positif. Le polynôme cyclotomique d'indice n est le polynôme à coefficient dans un corps premier contenant toutes les racines primitives n-ième de l'unité.
On le note en général Φn(X). Le symbole X désigne une indéterminée, les polynômes dont il est question ici sont formels et non pas des fonctions. Cette question est importante si le corps premier n'est pas le corps
-
- Un corps est dit premier s'il ne contient pas de sous-corps autre que lui-même.
C'est le plus petit sous-corps contenant 1 et tous ses itérés par l'addition. Si le corps est de caractéristique 0, il est égal à celui des nombres rationnels, sinon il est isomorphe à Z/pZ, où p est la caractéristique du corps.
Dans le cas des rationnels, si la séquence finie (zk) décrit les racines nième primitives de l'unité dans le corps des complexes et φ la fonction indicatrice d'Euler, le polynôme Φn(X) est donné par:
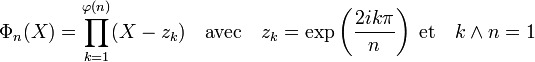
Les polynômes cyclotomiques sont des polynômes unitaires à coefficients entiers. De plus, il est possible d'appliquer à Φn le morphisme d'anneau de Z[X] dans Z/pZ[X]. En particulier, si p est un nombre premier, Z/pZ est un corps fini. Une telle approche est utilisée pour démontrer le caractère irréductible du polynôme précédent.
On appelle corps cyclotomique ou extension cyclotomique le plus petit sous-corps du corps des nombres complexes contenant tous les nombres rationnels et une racine primitive n-ième de l'unité. Au lieu de se placer dans le corps des complexes, on aurait pu considérer les racines primitives n-ièmes de l'unité dans n'importe quelle extension (finie ou infinie) du corps des rationnels dans laquelle au moins une telle racine primitive existe. une telle extension contient une copie du corps cyclotomique.
Dans le cas où le corps n'est pas celui des rationnels, alors il est de cardinal fini p et p est un nombre premier. Il correspond à la structure Z/pZ et il est noté Fp. La théorie de Galois assure l'existence d'un plus petit sur-corps de Fp contenant une racine primitive n-ième de l'unité, on l'appelle aussi extension cyclotomique. Une fois encore, tout corps de caractéristique p (c’est-à-dire contenant Fp) et possédant une racine primitive n-ième de l'unité contient une copie de l'extension cyclotomique.
Remarque : Les propriétés associées à la définition sont démontrées à la suite dans cet article.
Premiers polynômes cyclotomiques
Les premiers polynômes cyclotomiques dans le cas des nombres rationnels sont :
Contrairement aux apparences, tous les coefficients des polynômes cyclotomiques ne sont pas 1, -1 ou 0 ; le premier polynôme cyclotomique pour lequel un coefficient entier distinct de 0, 1, -1 apparait est Φ105. 105 = 3×5×7 est le premier produit de trois nombres premiers impairs.
En effet :
Dans le cas de la caractéristique finie, les polynômes précédents ne sont pas toujours irréductibles. On peut ainsi considérer le corps à deux éléments {0,1} noté F2. Il possède les tables d'opérations suivantes:
|
|
Le polynôme à coefficient dans Z Φ7(X) a pour image par le morphisme canonique dans F2[X] (qui aux coefficients pairs associe 0 et aux impairs 1) un polynôme qui possède bien les racines septièmes primitives de l'unité, mais ce polynôme n'est pas irréductible, en effet :
- Dans
![\quad \mathbb F_2[X]: \quad X^6+X^5+X^4+X^3+X^2+X+1=(X^3+X^2+1)(X^3+X+1)\;](https://static.techno-science.net/illustration/Definitions/autres/2/262905a7e3578b82ce458c7d54089911_442fe481d5d03a324a40f454c3cb7887.png)
![\quad \mathbb F_2[X]: \quad X^6+X^5+X^4+X^3+X^2+X+1=(X^3+X^2+1)(X^3+X+1)\;](https://static.techno-science.net/illustrationWebp/Definitions/autres/2/262905a7e3578b82ce458c7d54089911_442fe481d5d03a324a40f454c3cb7887.png)
D'autres exemples sont donnés dans le paragraphe Polynôme irréductible de l'article sur les corps finis.
