Polynôme cyclotomique - Définition

Propriétés remarquables

Cas du corps des nombres rationnels

Sans utiliser les outils sophistiqués que représente la théorie de Galois, il est possible de démontrer des propriétés fortes sur les polynômes cyclotomiques. Ce sont celles présentées dans ce paragraphe. Elles ont toutes été démontrées par Gauss dans son traité de 1801.

Pour un souci d'exposition, la définition initiale du polynôme cylotomique Φ_n(X) utilisée ici est, avec les notations de la définition :

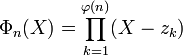
Les propriétés suivantes sont vérifiées:

• Le polynôme Xⁿ − 1 se factorise comme suit, où le produit porte sur l'ensemble des entiers strictement positifs qui divisent n :

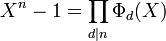
L'identité sur les degrés fournit immédiatement :

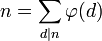
Cette identité peut aussi s'obtenir par des considérations sur la fonction de Möbius ou par un raisonnement direct de dénombrement des éléments de l'anneau Z/n Z (lire indicatrice d'Euler).

• Si p est un nombre premier, alors toutes les racines p-ièmes de l'unité sauf 1 sont des racines primitives p-ièmes primitives de l'unité, et l'égalité est vérifiée.

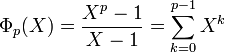
Cette égalité fournit une expression du polynôme cyclotomique, à l'aide de la formule d'inversion de Möbius. La démonstration est proposée dans l'article Fonction de Möbius. Ici la fonction de Möbius est notée μ :

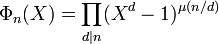
• Un polynôme cyclotomique ne possède que des coefficients entiers et son monôme dominant possède un coefficient égal à un.

• Un polynôme cyclotomique est irréductible dans l'algèbre des polynômes à coefficients rationnels et dans l'algèbre des polynômes à coefficients entiers.

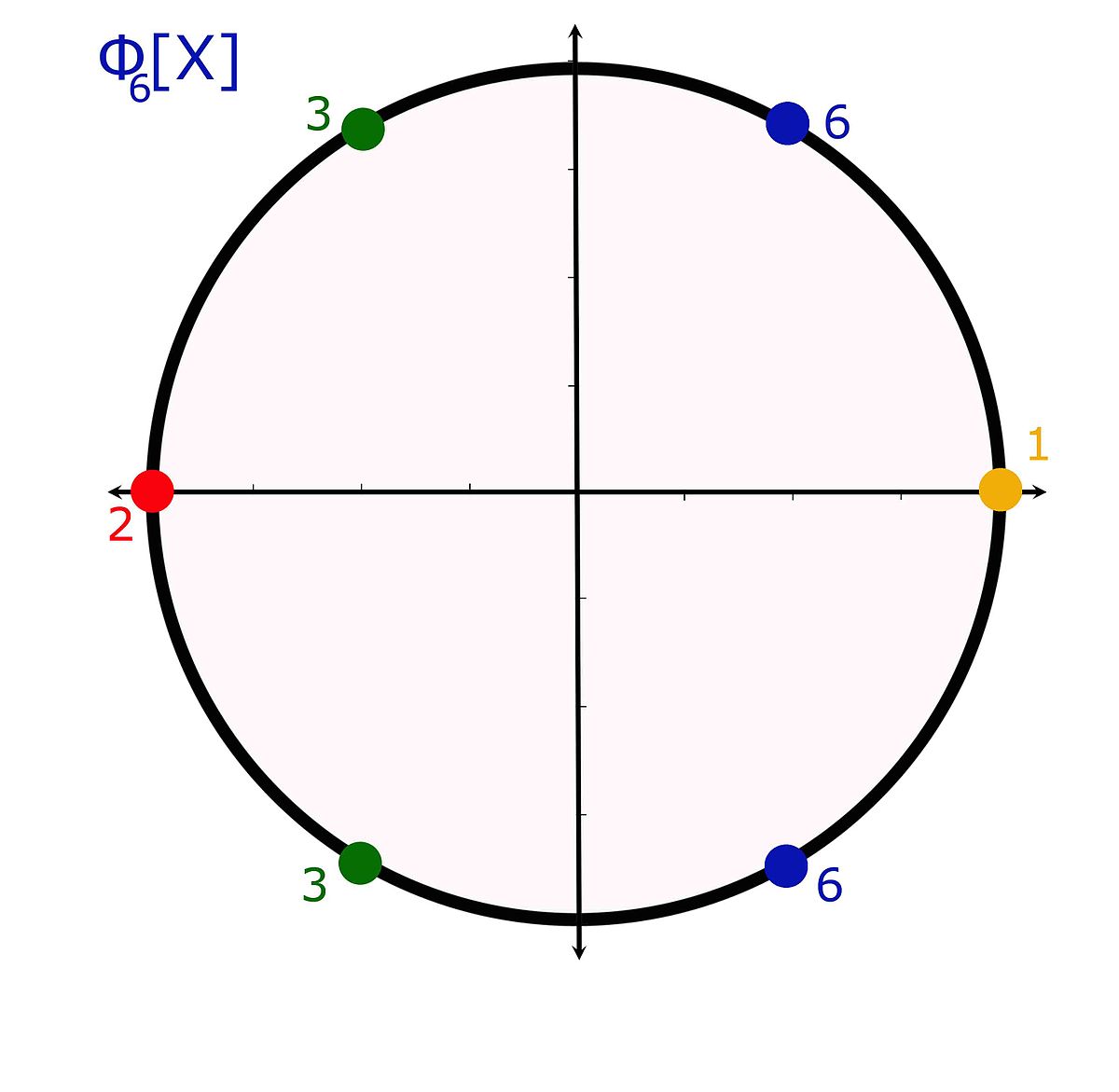
La figure de droite illustre ces propriétés. Le groupe des racines d'ordre six est décrit par quatre polynômes cyclotomiques, deux racines associées à des polynômes de degré un : un et deux, et quatre de degré deux avec les deux valeurs troisièmes et les deux valeurs sixièmes.

• Montrons l'égalité suivante:

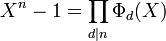
Les deux polynômes de l'égalité à démontrer sont des polynômes de monômes dominants égaux à un (polynômes unitaires). De plus ils sont de degré n. Il suffit donc de démontrer par exemple que le premier divise le second.

Le polynôme Xⁿ − 1 admet exactement n racines distincts, à savoir les n racines n-ièmes de l'unité. Étant de degré n, il n'admet donc aucune racine multiple. Il est donc simplement scindé, produit des monômes deux à deux premiers entre eux X-z où z parcourt les racines n-ièmes de l'unité. Or, toute racine n-ième est exactement une racine primitive d'ordre d pour un unique diviseur d de n. Par définition des polynômes cyclotomiques, z est une racine de Φ_d ; autrement dit, X-z divise Φ_d. De suite, Xⁿ divise le produit des Φ_d pour d divisant n.

L'égalité se trouve établie.

• Si p est un nombre premier, alors toutes les racines p-ièmes de l'unité sauf 1 sont des racines primitives p-ièmes de l'unité, et l'égalité suivante est vérifiée :

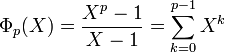
Si z est une racine primitive p-ième de 1, alors l'ordre de z dans le groupe multiplicatif C^* divise nécessairement p. Comme p est premier, l'ordre de z est 1 ou p. Le seul élément d'ordre 1 étant l'élément neutre 1, toute autre racine de p-ième est nécessairement une racine primitive d'ordre p.

Une autre preuve possible présuppose connu que l'indice d'Euler de p est p-1 : toutes les racines p-ièmes de l'unité sauf une doivent alors être primitives. Or 1 n'est une racine primitive d'un nombre premier. Ceci montre que le polynôme X^p - 1 n'admet que deux diviseurs X - 1 et le polynôme cyclotomique associé.

• Un polynôme cyclotomique Φ_n(X) ne possède que des coefficients entiers et de coefficient dominant égal à un.

Le fait que le coefficient dominant soit égal à un est une évidence.

Montrons par récurrence sur n que le polynôme est à coefficients entiers.

Si n est égal à 1 alors le résultat est vrai car Φ₁(X) = X - 1 (voir la section exemples).

Supposons la propriété vraie pour toute valeur inférieure ou égal à n. Alors la première proposition permet d'affirmer que:

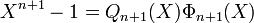
où le polynôme Q_n(X) est le produit de tous les polynômes cyclotomiques d-ièmes avec d divisant strictement n (ie d divise n et est distinct de n). Par hypothèse de récurrence, Q_n+1(X) est le produit de polynômes unitaires à coefficients entiers et donc lui-même un polynôme unitaire à coefficient entier. Divisons alors le polynôme à coefficients dans les entiers Xⁿ-1 par Q_n+1(X) dans l'anneau Z[X] des polynômes à coefficients entiers. Cela est réalisable car Q est unitaire ; on obtient alors l'identité:

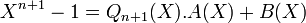
Avec A(X)et B(X) élément de Z[X], et B de degré strictement inférieur à n. Réalisons maintenant la division euclidienne dans l'anneau Q[X] l'anneau des polynômes à coefficients rationnels. Il existe une unique solution avec le degré de B(X) strictement inférieur à n+1. On en déduit que les divisions euclidiennes dans Q[X] et dans Z[X] donnent exactement le même résultat. En conséquence, B(X) est égal au polynôme nul et A(X) est égal au polynôme cyclotomique. Donc le polynôme cyclotomique est à coefficients entiers.

• Un polynôme cyclotomique est irréductible.

Soit z la première des racines primitives n-ièmes. C’est-à-dire z = exp(2π.i/n). Soit M₁(X) le polynôme minimal de z

M₁(X) est un polynôme à coefficients entiers unitaire.

z est racine du polynôme Xⁿ - 1 est donc son polynôme minimal divise ce polynôme. Il existe donc un polynôme à coefficients entiers tel que l'égalité suivante soit vérifiée:

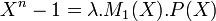
Où λ est choisi de telle manière à ce que le polynôme P(X) soit à coefficients entiers. La démonstration précédente a établi que dans ce contexte, λ.M₁ (X) est aussi un polynôme à coefficients entiers. De plus comme Xⁿ - 1 est unitaire, il en est de même pour M₁ (X) et P(X) et λ est égal à 1.

Si p est un nombre premier qui ne divise pas n alors z ^p est racine de M₁(X).

Raisonnons par l'absurde et supposons que cela ne soit pas le cas. Soit M_p (X) le polynôme minimal de z ^p alors M_p (X) ne divise pas M₁ (X) mais divise Xⁿ - 1. Il divise donc le polynôme P(X). Il existe donc un polynôme Q(X) vérifiant l'égalité suivante:

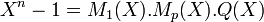
Un raisonnement analogue à celui sur P(X) montre que Q(X) est unitaire à coefficients entiers. z ^p est racine du polynôme M_p (X) et donc z est racine du polynôme M_p [X^p]. On en déduit que M_p [X^p] est un multiple de M₁ (X). Il existe donc un polynôme unitaire R(X) à coefficients entiers vérifiant:

Par passage au modulo p, en remarquant que la formule du binôme devient

en conséquence

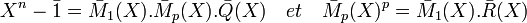
Soit D(X) un diviseur irréductible de degré strictement supérieur à 1 de M₁ (X) dans l'anneau quotient, alors il divise aussi M_p (X) dans l'anneau quotient puisqu'il divise sa puissance. On en déduit que son carré divise Xⁿ - 1 et D(X) divise la dérivée formelle de Xⁿ - 1 dans l'anneau quotient (cf l'article polynôme formel). D(X) divise donc nX^n-1 dans l'anneau quotient, et ce polynôme est non nul car n et p sont premiers entre eux. On en déduit que D(X) est égal à X car il est irréductible. Or X ne divise pas Xⁿ - 1 dans l'anneau quotient. D'où une contradiction. En conséquence nous avons montré que M_p (X) est égal à M₁ (X).

Si k est un nombre premier avec n alors z ^k est racine de M₁(X).

Le nombre k est produit de q nombres premiers qui ne divisent pas n. Une récurrence sur q permet de conclure. Si q vaut 1, la proposition précédente permet de conclure. En supposant la propriété vraie pour le rang q-1, si z' est égal à z à la puissance le produit de q-1 nombres premiers ne divisant pas n, z' est racine de M₁ (X) et le raisonnement précédent montre que z' à la puissance un nombre premier ne divisant pas n est encore racine de M₁ (X), donc z à la puissance le produit de q nombres premiers ne divisant pas n est racine de M₁ (X).

En conclusion, le polynôme minimal de z contient pour racine au moins toutes les racines du polynôme cyclotomique. Le polynôme cyclotomique divise donc le polynôme minimal. Comme ce dernier est irréductible, l'égalité est établie.

 

Cas de la caractéristique finie

Corps de décomposition

Soit p la caractéristique du corps premier, ce corps est celui de l'arithmétique modulaire isomorphe à Z/p.Z. On peut considérer dans un tel corps un polynôme du type Xⁿ - 1, par exemple dans F₂[X] le polynôme X³ - 1. Dans le cas de , il existe une extension de corps celui des nombres complexes contenant les racines du polynôme. La théorie de Galois, à l'aide des extensions algébriques permet de trouver une extension dans lequel le polynôme est scindé, c’est-à-dire que l'extension contient toutes ses racines. Un tel corps est appelé corps de décomposition. Dans l'exemple cité, le corps est celui noté en général F₄ contenant quatre éléments. Sa table est la suivante:

Illustration graphique du groupe multiplicatif de F₄

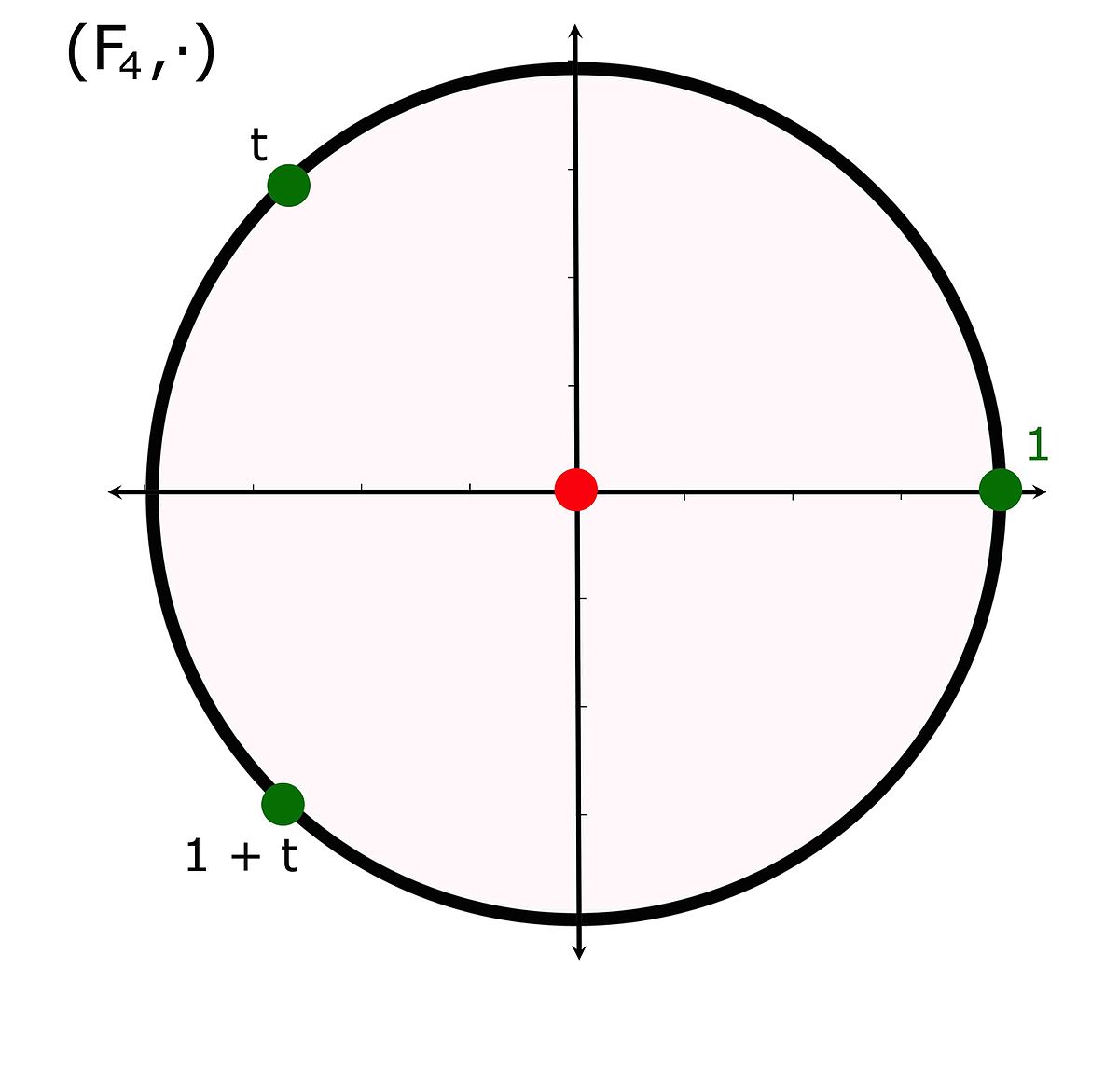
Dans ce corps, t et 1 + t sont les deux racines supplémentaires du polynôme X³ - 1. L'étude des extensions algébriques montre que tout corps contenant les racines d'un polynôme contient un sous corps isomorphe à F₄. En conséquence tout corps de caractéristique deux contenant les racines possède une copie exacte de F₄. Les solutions trouvées et leur comportement algébrique sont donc toujours les mêmes. Ce résultat est général à toute extension finie et donc à tout polynôme cyclotomique.

La théorie des corps finis permet d'aller plus loin. Les seules extensions d'un corps premier F_p sont une extension de cardinal une puissance de p et il existe une et une unique extension de cardinal p^m où m est un entier strictement positif. De plus, le groupe multiplicatif d'une telle extension est un groupe cyclique de cardinal pⁿ - 1 (0 n'est pas élément du groupe multiplicatif car il n'a pas d'inverse). La figure de droite l'illustre dans le cas de F₄, tout élément autre que 0 apparaît comme une racine de l'unité. La multiplication est représentée graphiquement comme on le fait pour le corps des complexes. En revanche, l'addition n'est pas représentée.

Automorphisme de Frobenius

Ferdinand Georg Frobenius

Dans le cas d'un corps fini de caractéristique p et de cardinal p^d il existe un automorphisme digne d'intérêt: l'automorphisme de Frobenius. À un élément x du corps il associe x^p. Cet automorphisme est un générateur du groupe de Galois et sa d-ième puissance est égale à l'identité. Pour cette raison et dans ce contexte on appelle souvent le groupe de Galois groupe de Frobenius. Cette égalité se traduit en terme polynomial par:

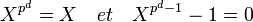
Et tout élément du corps différent de zéro est une racine de l'unité. Un polynôme irréductible autre de X (qui admet pour racine zéro) est un polynôme cyclotomique. La détermination des polynômes cyclotomiques correspond donc à un classement des polynômes irréductibles. On en déduit la proposition suivante:

• Tout élément non nul d'un corps fini est une racine de l'unité et tout polynôme irréductible différent que X est un polynôme cyclotomique.

Soit z₁ une racine primitive n-ième de l'unité. La théorie de Galois démontre que son polynôme minimal admet pour racines les images de z₁ par le groupe de Frobenius, car un corps fini est une extension galoisienne du corps premier. Ce qui se traduit en termes mathématiques

• L'ensemble des racines du polynôme cyclotomique de z₁ est l'orbite de z₁ par l'action du groupe de Frobenius notée Orb (z₁). La formule du polynôme est la suivante:

L'image par un automorphisme d'une racine n-ième primitive de l'unité est une racine primitive n-ième de l'unité, et:

• Un polynôme cyclotomique d'indice n divise l'image du polynôme cyclotomique à coefficients entiers par le morphisme canonique de Z[X] dans F_p[X].

Il reste à savoir si les deux polynômes sont égaux, c’est-à-dire si l'orbite de z₁ contient toutes les racines primitives n-ième de l'unité. L'exemple donné sur F₂ montre que ce n'est pas toujours le cas. La théorie de Galois permet d'affirmer que le degré du polynôme cyclotomique de z₁ est la dimension δ du corps de décomposition, considéré comme un espace vectoriel sur le corps primitif. Le corps de décomposition est un ensemble de cardinal p^δ. Son groupe multiplicatif est un groupe cyclique d'ordre p^δ -1. L'analyse des groupes cycliques montre que ce groupe contient les racines n-ième de l'unité si et seulement si son cardinal est un multiple de n. En conséquence δ est égal à l'ordre multiplicatif de p modulo n, c’est-à-dire le plus petit entier δ tel que p^δ-1 soit un multiple de n.

• Un polynôme cyclotomique d'indice n sur F_p est de degré l'ordre multiplicatif de p modulo n.

Le théorème d'Euler montre que:

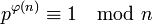
Cependant, l'ordre multiplicatif de p modulo n est égal à φ(n) si et seulement si n - 1 n'est pas un multiple de p. Dans l'exemple précédent, p est égal à 2, n à sept, φ(n) égale six, un multiple de p. Le théorème d'Euler est bien vérifié car soixante quatre est congru à un modulo sept, mais l'ordre multiplicatif est égal à trois car huit est congru à un modulo sept.

• Si δ désigne l'ordre multiplicatif de p modulo n, il existe φ(n)/δ polynômes cyclotomiques d'indice n sur F_p. Leur degré est égal à δ et leur produit est l'image du polynôme cyclotomique d'indice n à coefficients dans Z par le morphisme canonique de Z[X] dans F_p[X].

Des exemples sont donnés dans l'article corps fini.