Polynôme cyclotomique - Définition
La liste des auteurs de cet article est disponible ici.
Extension cyclotomique
L'extension cyclotomique est par définition le corps de rupture d'un polynôme cyclotomique, c’est-à-dire le plus petit corps contenant une racine primitive n-ième d'un polynôme cyclotomique. (Rappelons qu'un corps de rupture d'un polynôme est une extension de corps permettant une factorisation de ce polynôme.) Il possède des propriétés fortes, à l'origine de nombreuses applications:
-
- L'extension cyclotomique est un espace vectoriel sur le corps des nombres rationnels de dimension φ(n).
Cette propriété est générale aux corps de ruptures. La démonstration est donnée dans l'article Extension algébrique.
-
- L'extension cyclotomique est aussi le corps de décomposition du polynôme. Elle est donc galoisienne.
Cela signifie que le plus petit corps contenant une racine du polynôme contient aussi toutes les racines du polynôme. Dire que ce corps est une extension galoisienne signifie deux choses: d'une part, les polynômes minimaux de ce corps n'ont pas de racines multiples (ce qui est toujours vraie pour les extensions sur les nombres rationnels) ; et d'autre part, tous les morphismes de ce corps dans les nombres complexes ont pour image le corps lui-même. Ce sont donc des automorphismes. Ils forment une structure de groupe appelé groupe de Galois. La théorie de Galois indique que c'est la bonne structure pour rechercher une expression des racines par radicaux.
-
- L'extension cyclotomique est abélienne.
Cela signifie que le groupe de Galois est commutatif (ou abélien). L'équation polynomiale cyclotomique est alors résoluble par radicaux. Autrement dit, les solutions s'expriment à l'aide des uniques quatre opérations (additionner, soustraire, diviser et multiplier) et des racines p-ième appliquées un nombre fini de fois sur des nombres rationnels et l'imaginaire pure i. Ce résultat est connu sous le nom de théorème d'Abel. Il est ainsi possible par exemple de résoudre par radicaux l'équation cyclotomique donnant la racine dix-septième de l'unité. C'est une condition nécessaire pour la résolution de la construction par la règle et le compas du polygone régulier à dix-sept côtés (voir ci-dessous).
-
- L'extension cyclotomique est une tour d'extension quadratique si et seulement si n est de la forme suivante:
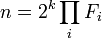
- Où les Fi sont des nombres premiers de Fermat distincts.
Ce résultat est aussi connu sous le nom de Théorème de Gauss-Wantzel. Une tour d'extension quadratique est un corps tel que pour chaque élément x du corps, il existe une suite de sous-corps K0, K1, ..., Kp avec K0 égal au corps de base, ici celui des rationnels, Kp contient x, et, pour tout i entre 1 et p, Ki contient Ki - 1 et est un espace vectoriel de dimension 2 sur Ki - 1.
Dire que Ki contient Ki - 1 et est un espace vectoriel de dimension 2 sur Ki - 1 revient seulement à dire que tout élément de Ki s'exprime comme la somme d'un nombre de Ki - 1 et d'une racine carré d'un nombre de Ki - 1. En particulier, tout élément de Ki s'exprime comme racine d'un polynôme de degré 2 sur Ki-1. Cette propriété est démontrée dans l'article Extension quadratique.
Or l'article sur les nombres constructibles montre qu'un point est constructible si et seulement s'il vérifie cette propriété. Cette propriété permet donc de déterminer la liste des polygones constructibles et assure qu'ils le sont effectivement.
Un nombre premier de Fermat est un nombre premier de la forme
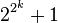
-
- L'extension cyclotomique est aussi le corps de décomposition du polynôme. Elle est donc une galoisienne.
L'extension contient z et donc toutes ses puissances, or les puissances de z forment l'ensemble des racines n-ièmes de l'unité et donc en particulier les racines primitives qui sont les racines du polynôme cyclotomique. Ceci démontre que Q[z] est le corps de décomposition. Dans un corps parfait comme celui des rationnels (un corps parfait est un corps où tous les polynômes irréductibles sont séparables c’est-à-dire n'ont pas de racines multiples dans la clôture algébrique) un corps de décomposition est toujours une extension de Galois.
-
- L'extension cyclotomique est abélienne.
Soit d un entier plus petit que n et qui ne divise pas n. Alors zd est une racine du polynôme cyclotomique et il existe au moins un morphisme qui envoie z sur zd (cf première proposition du paragraphe Extension algébrique et sur-corps). Il n'existe qu'un unique moyen de prolonger sur l'extension le morphisme md qui à z associe zd. En effet md(zi) = md(z)i = z i.d. Or la famille des z i si i varie de 0 à φ(n) - 1 forme une base de l'extension. Les automorphismes du groupe de Gallois sont donc parfaitement déterminés.
Considérons alors l'application du groupe multiplicatif des éléments inversibles de
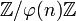
-
- Condition nécessaire pour que l'extension soit une tour d'extension quadratique.
Par définition d'une tour d'extension quadratique, une condition nécessaire est que la dimension de l'extension soit une puissance de deux. Étudions alors les entiers n tel que φ(n) soit une puissance de deux.
Remarquons tout d'abord que si n est égal à p.q avec p et q premiers entre eux alors nous avons l'égalité suivante φ(n) = φ(p).φ(q) (cf l'article Indicatrice d'Euler). Considérons alors la décomposition de n en facteur premier (cf l'article Théorème fondamental de l'arithmétique).
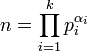
L'indicatrice d'Euler d'une puissance d'un nombre premier pα est égale à (p - 1). pα -1. Il suffit donc de trouver une condition nécessaire et suffisante pour que le facteur (p - 1). pα -1 soit une puissance de deux et appliquer cette condition à chacun des facteurs de l'égalité précédente. Deux cas se présentent, soit p est égal à 2 et toute valeur de α est acceptable, soit p est un nombre premier de la forme 2k + 1 avec k un entier strictement positif et α est égal à 1.
Montrons par contraposé que si p est un nombre premier de la forme 2k + 1 alors k est une puissance de deux. Si tel n'est pas le cas, alors il existe deux entiers a et b tel que k = a . 2b où a est un entier impair et b un entier. L'égalité suivante est vérifiée p = 1 + ca ou c = 2b. Dans ce cas, comme a est impair, on a l'égalité:
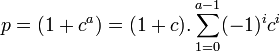
L'égalité précédente montre que 1 + c est un diviseur de p. Par contraposé, si p est premier, il est donc égal à un nombre de Fermat.
En conclusion n est de la forme suivante:
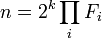
Où les Fi sont des nombres premiers de Fermat distincts. Et la condition nécessaire est démontrée.
-
- Condition suffisante pour que l'extension soit une tour d'extension quadratique.
Le polynôme cyclotomique est alors de degré φ(n) et est une puissance de deux. Notons 2k ce degré. Le groupe de Galois est alors le groupe cyclique de cardinal 2k.
Montrons que si l est un entier inférieur à k il existe un sous-groupe Gl du groupe cyclique de cardinal 2l et tel que si l est non nul alors Gl - 1 est inclus dans Gl. Définissons Gl comme le sous-groupe engendré par la classe de 2k-l. Par définition Gl - 1 est inclus dans Gl si l est non nul. De plus le cardinal de Gl est clairement égal à 2k-l.
On remarque ensuite que Gl-1 est un sous-groupe distingué de Gl car ce sont des groupes abéliens, donc tout sous-groupe est distingué. Ensuite le cardinal du groupe quotient de Gl par Gl - 1 est deux.
Le théorème fondamental de la théorie de Galois assure que si Kk- l est le sous-corps de l'extension qui laisse invariant tous les automorphismes de Gl (on a ici identifié le groupe de Galois et le groupe cyclique) alors si l est non nul Kl est une extension galoisienne de Kl - 1 de dimension deux donc quadratique, que K0 est égal au corps des nombres rationnels et que Kk est le corps de décomposition du polynôme cyclotomique.
Nous avons donc monté une tour d'extension quadratique du corps de décomposition et le théorème est démontré.