Arithmétique des polynômes - Définition

Introduction

En algèbre, l'arithmétique des polynômes décrit les propriétés des polynômes qui peuvent se déduire de l'arithmétique et qui sont un peu analogues à celles des nombres entiers. Par exemple, l'anneau des polynômes K[X] à une indéterminée X et à coefficients dans un corps commutatif K dispose d'une division euclidienne. Si le lecteur n'est pas familier avec les structures de corps et d'anneau, il peut considérer K comme une lettre symbolisant l'ensemble des nombres réels ou complexes. La division euclidienne est à l'origine des théorèmes clés de l'arithmétique élémentaire. Il en est de même pour l'arithmétique des polynômes. On démontre de la même manière l'identité de Bézout, le lemme d'Euclide ou un équivalent du théorème fondamental de l'arithmétique, les polynômes irréductibles et unitaires prenant alors la place des nombres premiers.

Ces résultats ne s'appliquent plus de la même manière si les coefficients sont choisis dans un ensemble A comme celui des nombres entiers, où les éléments ne sont pas toujours inversibles pour la multiplication. L'étude de cette configuration demande l'usage d'un attirail d'outils mathématiques plus puissants. Ils permettent de montrer que si l'identité de Bézout n'est plus vérifiée, un équivalent du théorème fondamental de l'arithmétique reste encore valable. Cette propriété reste vraie si l'anneau comporte plusieurs indéterminées. Autrement dit, si A est un anneau factoriel, l'anneau des polynômes à coefficients dans A est aussi factoriel, quel que soit le nombre d'indéterminées. Dans certains cas, l'anneau A n'est pas factoriel mais juste noethérien. À condition que l'anneau des polynômes ne contienne qu'un nombre fini d'indéterminées, il est aussi noethérien.

Ces différents résultats sont à l'origine de théorèmes fondateurs de diverses branches de l'algèbre. La théorie de Galois s'appuie sur la structure euclidienne de K[X], la théorie algébrique des nombres fait usage du caractère factoriel et noethérien d'un anneau de polynômes à une ou plusieurs indéterminées sur un anneau factoriel. Enfin, des théorèmes comme celui de la base de Hilbert ou le Nullstellensatz, essentiels en géométrie algébrique, sont des conséquences directes de l'arithmétique des polynômes.

Corps commutatif

Dans le reste de l'article K désigne un corps commutatif. Ce corps peut être égal à Q celui des nombres rationnels, R celui des réels ou C pour les complexes, ou encore un corps fini. Dans ce paragraphe tous les polynômes sont en une indéterminée et à coefficients dans K, l'anneau de ces polynômes est noté K[X]. L'anneau K[X] possède une division euclidienne (cf l'article Division d'un polynôme) et comme pour tout anneau euclidien, les conséquences sont multiples. Elles sont exactement semblables à celle traitées dans l'article arithmétique élémentaire, qui traite de l'arithmétique des nombres entiers.

Il est possible d'exprimer ces résultats sous deux formes, la première et la plus simple est celle utilisé dans l'article arithmétique élémentaire. La deuxième, emploie le vocabulaire de la théorie des anneaux, c'est-à-dire des termes comme idéal, idéal principal, premier ou encore maximal. L'article explicite les résultats dans les deux langages.

Identité de Bézout

Suivre le plan de l'article Arithmétique élémentaire, suppose dans une premier temps de s'intéresser aux sous-ensembles de K[X] non vide et stable pour l'addition et la soustraction. Pour que les conséquences soient aussi riche que dans l'article sur les entiers, il est nécessaire d'ajouter la stabilité de l'ensemble par multiplication par un polynôme quelconque. On obtient le résultat suivant :

En termes de théorie des anneaux, ce résultat indique que K[X] est un anneau principal, ce qui est le cas de tout anneau euclidien. La démonstration se trouve dans l'article Anneau euclidien.

La conséquence directe est :

Identité de Bézout — Soit P et Q deux polynômes, P et Q sont premiers entre eux si, et seulement si, il existe deux polynômes M et N tel que :

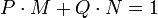
Il devient nécessaire de définir l'expression polynômes premiers entre eux. Deux polynômes sont premiers entre eux lorsque les seuls polynômes qui les divisent tous les deux sont les polynômes constants non nuls. Cette définition est très proche de celle des entiers qui sont premiers entre eux lorsque les seuls diviseurs communs sont 1 et -1, c'est-à-dire les éléments inversibles de l'anneau.

Dans le vocabulaire des anneaux, l'identité se traduit un peu différemment. Soit A et B deux idéaux de K[X], si l'intersection de A et de B est égal au produit des idéaux A.B (ce qui est l'équivalent de l'expression premiers entre eux), alors l'idéal A + B est égal à K[X].

Polynôme irréductible

Continuer l'analogie avec l'arithmétique élémentaire demande à ce niveau de disposer d'un équivalent des nombres premiers. Dans Z, un nombre premier n'est divisible que par 1, -1 ou le produit d'un de ces deux éléments et de lui-même. Cependant ces nombres ne sont que qualifiés d'irréductibles. Pour qu'ils soient déclarés premiers il faut en plus qu'ils soient positifs. Ce qui caractérise un nombre premier, ce sont ces multiples, or 2 et -2 ont le même ensemble de multiples, ce qui forme une classe d'équivalence dont la relation R est définie par : a et équivalent à b lorsque a et b possèdent le même ensemble de multiples. Dans le cas général, deux éléments d'un anneau a et b sont équivalents, ou encore ont le même ensemble de multiples, s'il existe un élément c inversible pour la multiplication, tel que a.c = b. Dans Z, les deux seuls éléments inversibles sont 1 et -1. On dit qu'ils sont éléments du groupe des unités et les éléments inversibles sont dits des unités. La relation d'équivalence est étudiée dans l'article Groupe des unités. Dans le cas des polynômes :

On en déduit une définition pour les polynômes, presque équivalente à celle des nombres premiers :

On dispose, par exemple de la proposition :

Pour exprimer l'équivalent théorème fondamental de l'arithmétique, il est important de choisir un unique nombre premier dans chaque classe d'équivalence, pour la relation R, de nombres irréductibles. Dans Z, il suffit d'indiquer qu'un nombre irréductible est dit premier s'il est positif, car chaque classe d'équivalence contient deux éléments : a et son opposé -a. La même relation d'équivalence dans K[X] existe et la classe d'équivalence d'un polynôme P est l'ensemble des polynômes k.P si k décrit tous les éléments de K non nuls. Pour exprimer l'équivalent du théorème fondamental de l'arithmétique, on choisit généralement l'élément de la classe qui est unitaire, c'est-à-dire celui dont le coefficient du monôme dominant (celui du plus haut degré) est égal à 1. Dans chaque classe d'équivalence de polynôme irréductible, il n'existe en effet qu'un unique polynôme unitaire.

Théorème fondamental de l'arithmétique

Avant d'énoncer le théorème fondamental, un premier lemme est utile :

En termes d'anneau, ce résultat s'exprime comme par : Si un idéal premier I contient le produit de deux idéaux A et B il est contient soit A soit B , proposition toujours vraie dans un anneau principal (cf l'article Idéal premier).

On obtient finalement le théorème suivant :

Autrement dit, en termes d'anneau, K[X] est factoriel, car tout anneau principal est factoriel (cf l'article Anneau factoriel).

Arithmétique modulaire

Une structure digne d'intérêt sur les entiers est celle du quotient Z/nZ. Un élément de ce quotient est représenté par un reste de division euclidienne d'un entier quelconque par n, on trouve toujours un représentant unique d'une congruence modulo n dans les entiers positifs strictement plus petit que n. Si p est un entier irréductible (c'est-à-dire un nombre premier ou son opposé), la structure Z/pZ est un corps, autrement dit, tout élément non nul de Z/pZ est inversible.

Soit P un polynôme irréductible, il est tentant de considérer les polynômes de K[X] modulo P. On obtient une structure avec une addition et une multiplication, qui vérifie toutes les propriétés d'un anneau commutatif unitaire, exactement comme celle décrite dans l'article Congruence sur les entiers. On dispose encore de la propriété :

Notons L la structure des congruences sur les polynômes de K[X] modulo P. Comme tout élément différent de 0 est inversible pour la multiplication, on dit que c'est un corps. Il est appelé le corps de rupture de K. Ce corps dispose d'une propriété remarquable :

• Si P est un polynôme irréductible de K[X], toute congruence modulo P non nul possède un inverse pour la multiplication :

Pour s'en rendre compte, considérons un polynôme M de K[X] dont la congruence n'est pas nulle, modulo P. Autrement dit, le reste de la division de M par P n'est pas nul, ce qui revient à dire que P ne divise pas M. Comme P est irréductible, cela revient aussi à dire que M et P sont premiers entre eux, l'identité de Bézout montre qu'il existe deux polynômes A et B tel que :

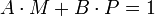
En termes de congruence, cela signifie que :

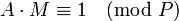
Cette égalité signifie exactement que la congruence de A est l'inverse pour la multiplication de la congruence de M modulo P.

• Le corps L dispose d'une structure de K espace vectoriel de dimension le degré de P :

Le corps L dispose d'une multiplication externe sur le corps des scalaires K, de manière naturelle. Si k désigne un scalaire de K et M_c la congruence modulo P représenté par le polynôme M, le produit k.M_c est la congruence représenté par le polynôme k.M. Il est simple de vérifier que cette multiplication externe définit bien une structure d'espace vectoriel sur L, muni de l'addition.

Il faut encore exhiber une base, pour calculer sa dimension. Notons χ la congruence de l'indéterminée X modulo P et B la famille (1, χ,  χ², ...,  χ^n-1) et montrons que B est une base de L, considéré comme un K espace vectoriel.

La famille B est libre. En effet, soit une combinaison linéaire nulle de cette famille :

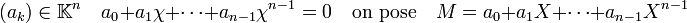
Cette combinaison linéaire de L est le représentant du polynôme M, défini à la ligne précédente, dans les congruences modulo P. La congruence de M est nulle modulo P, ce qui signifie que M est un multiple de P. Le polynôme M est un multiple de P de degré strictement inférieur à P, ce qui montre que M est le polynôme nul et que la combinaison linéaire est triviale.

Il ne reste plus qu'à montrer que :

La famille B est génératrice. Soit N un polynôme quelconque de K[X] et R le reste de la division euclidienne de N par P. R est un polynôme de degré strictement inférieur à n et congru à N modulo P. La congruence de R, R_c s'écrit encore :

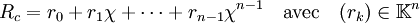
Ce qui revient à dire que la congruence de R et donc celle de N est une combinaison linéaire de la famille B, et termine la démonstration.