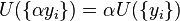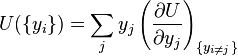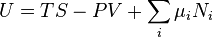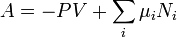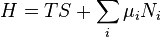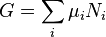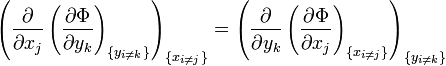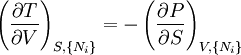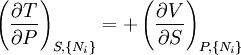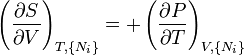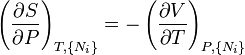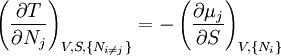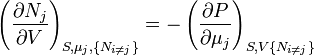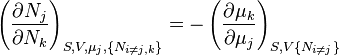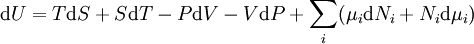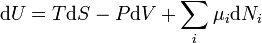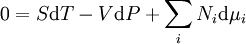Potentiel thermodynamique - Définition

Intégrales d'Euler

A nouveau, on définit x_i et y_i comme des paires conjuguées, et y_i comme les variables naturelles de l'énergie interne. Comme toutes les variables naturelles de l'énergie interne U sont des grandeurs extensives :

d'après le Théorème d'Euler pour les fonctions de plusieurs variables, l'énergie interne peut être écrite sous la forme :

L'équation d'état nous donne :

Par substitution dans les expressions des autres potentiels thermodynamiques, on obtient :

Comme dans les sections précédentes, on peut effectuer cette suite de calculs avec tous les autres potentiels thermodynamiques. Les intégrales d'Euler sont parfois appelées équations fondamentales.

Relations de Maxwell

A nouveau, on définit x_i et y_i comme des variables conjuguées et y_i comme les variables naturelles d'un potentiel Φ. En prenant les "différentielles croisées" des équations d'état, qui obéissent à la relation :

on obtient les relations de Maxwell. Il y a (D-1)/2 relations pour chaque potentiel, soit un total de D(D-1)/2 équations au total. En se limitant à U, A, H, et G, on a :

En utilisant les équations d'état incluant le potentiel chimique, on obtient des équations telles que :

et en utilisant les autres potentiels, on obtient des équations telles que :

Réactions chimiques

Les variations de ces grandeurs sont utiles pour décrire le degré d'avancement d'une réaction chimique. La grandeur appropriée dépend des conditions de réaction, comme le montre le tableau suivant :

	V constant	P constante
S constante	ΔU	ΔH
T constante	ΔA	ΔG

On considère souvent les réactions à P et T constantes, c'est donc l'enthalpie libre de Gibbs qui sera le potentiel le plus utile pour étudier la réaction chimique.

La relation de Gibbs-Duhem

En différentiant l'équation d'Euler pour l'énergie interne ci-dessus, on a :

Or l'équation fondamentale pour U énonce que :

Par soustraction, on obtient la relation de Gibbs-Duhem :

La relation de Gibbs-Duhem, établie par Josiah Gibbs et Pierre Duhem, est une relation entre les paramètres intensifs du système. Il en découle que pour un système simple à r composants, il y aura r+1 paramètres indépendants, ou degrés de liberté. Par exemple, un système simple avec un composant unique a deux degrés de liberté, et peut être décrit par deux paramètres, comme la pression et le volume par exemple.

Références de l'article anglais

• Alberty, R. A., « Use of Legendre transforms in chemical thermodynamics », dans Pure Appl. Chem., vol. Vol. 73, n^o 8, 2001, p. 1349–1380  

• Callen, Herbert B. (1985). Thermodynamics and an Introduction to Themostatistics, 2nd Ed., New York: John Wiley & Sons. ISBN 0-471-86256-8.