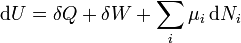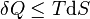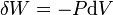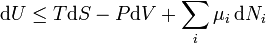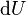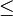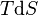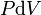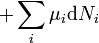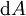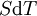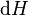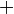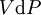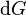Potentiel thermodynamique - Définition
La liste des auteurs de cet article est disponible ici.
Equations d'état
On peut utiliser les équations ci-dessus pour en dériver les définitions différentielles de quelques grandeurs thermodynamiques. Si l'on note Φ un potentiel thermodynamique quelconque, alors les équations précédentes sont de la forme :
où xi et yi sont des paires conjuguées, et les yi sont les variables naturelles du potentiel Φ. D'après la règle de dérivation en chaîne :
où
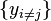
où, dans la dernière équation, φ est un potentiel thermodynamique parmi U, A, H et G, et
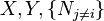
etc... Au total, il y a D équations pour chaque potentiel, soit D×2D équations d'état. Si les D équations d'état pour un potentiel particulier sont connues, alors l'équation fondamentale pour ce potentiel peut être déterminée. Ceci signifie que toutes les informations thermodynamiques sur le système peuvent être connues et que les équations fondamentales de chaque potentiel peuvent être déterminées.
Équations fondamentales
Les définitions des potentiels thermodynamiques peuvent être différentiées, et l'on peut obtenir un ensemble d'équations différentielles connues sous le nom d'« équations fondamentales ».
D'après le premier principe de la thermodynamique, une variation différentielle de l'énergie interne U d'un système peut s'écrire comme la somme d'une quantité de chaleur fournie au système, de travail fourni à l'environnement par le système, et d'un terme dû à l'apport de nouvelles particules au système :
où δQ est la quantité infinitésimale de chaleur fournie au système, δW est le travail infinitésimal fourni par le système, µi est le potentiel chimique des particules de type i, et Ni est le nombre de particules de type i (ni δQ ni δW sont des différentielles exactes. Des petites variations de ces grandeurs sont donc représentées par δ plutôt que par d).
D'après le second principe de la thermodynamique, on peut exprimer les variations d'énergie interne grâce à des fonctions d'état et leurs différentielles :
où T est la température, S l'entropie, P la pression et V le volume (l'égalité est obtenue pour les transformations réversibles).
Ceci nous mène à la forme différentielle standard de l'énergie interne :
En appliquant la transformation de Legendre, les relations différentielles pour les autres potentiels thermodynamiques principaux sont donc :
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
Pour chaque équation, les différentielles du membre de droite sont les variables naturelles du potentiel décrit au membre de gauche. Ces relations montrent que quand les variables naturelles de chaque potentiel sont maintenues constantes, la valeur du potentiel diminue de manière irréversible, vers sa valeur minimale constante à l'équilibre.
Des équations similaires peuvent être développée pour les autres potentiels thermodynamiques du système. Il y a une équation fondamentale pour chaque potentiel thermodynamique, soit au final 2D équations fondamentales.
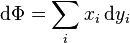
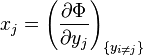
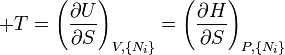
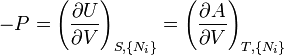
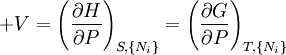
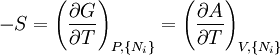
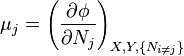
![-N_j=\left(\frac{\partial U[\mu_j]}{\partial \mu_j}\right)_{S,V,\{N_{i\ne j}\}}](https://static.techno-science.net/illustration/Definitions/autres/3/3c18bf0022d4ea560cad992fb8ec60e5_3b5b3cf1aa6ba77cba7726147d534c83.png)