Produit tensoriel de deux modules - Définition

Introduction

Le produit tensoriel de deux modules est une construction en théorie des modules qui à deux modules sur un même anneau assigne un module. C'est une construction abstraite qui est plus simple à assimiler en se limitant dans un premier temps au cas des espaces vectoriels. Le produit tensoriel est très important dans le domaine de la topologie algébrique et de la géométrie algébrique. Le produit tensoriel permet en outre de ramener l'étude d'applications bilinéaires ou multilinéaires à des applications linéaires.

Introduction - applications bilinéaires

Lorsque M, N et F sont trois modules sur un même anneau commutatif unitaire A, on appelle application bilinéaire une application f : M × N → F, telle que :

• f est linéaire à gauche, c'est-à-dire que .
• f est linéaire à droite, c'est-à-dire que .

Les applications bilinéaires sont des objets mathématiques compliqués, c'est pourquoi on peut être tenté de ramener le problème des applications bilinéaires à celui des applications linéaires. En d'autres termes, existe-t-il un module et une application bilinéaire tels que toute application bilinéaire se factorise de manière unique à droite par , c'est-à-dire qu'il existe une et une seule application linéaire telle que .

On peut prouver qu'un tel couple existe et est unique à unique isomorphisme près.

Généralisation à un produit fini de modules

Ce qui a été fait précédemment se généralise sans peine aux applications multilinéaires. Soit n modules sur un même anneau commutatif unitaire A. On considère le module produit . Une application f : E → F est dite n-linéaire si

Quels que soient l'indice i et les n - 1 éléments , l'application partielle est linéaire.

Il existe un A-module que l'on note et une application n-linéaire surjective de E dans telle que pour toute application n-linéaire de E dans un module d'arrivée F, il existe une unique application linéaire telle que .

En fait, le produit tensoriel de deux modules est associatif au sens suivant : si E, F, G sont trois modules sur un anneau commutatif unitaire A, alors les modules , et sont isomorphes.

Définition

Soit M et N deux modules sur un même anneau commutatif unitaire A. L'espace est le A-module des combinaisons linéaires formelles d'éléments de M × N. C est un A-module libre dont est la base canonique.

On souhaite que les éléments de la forme

• e_{(x + y,z)} − e_(x,z) − e_(y,z)
• e_{(x,y + z)} − e_(x,y) − e_(x,z)
• e_(αx,y) − αe_(x,y)
• e_(x,αy) − αe_(x,y)

soient identifiés comme nuls. On appelle donc D le sous-module de C engendré par les éléments de la forme précédente. On appelle produit tensoriel de M et N, et on note le module quotient C/D. Il est important de préciser l'anneau des scalaires A dans la notation du produit tensoriel. Néanmoins, si la situation est assez claire, on peut se permettre de ne pas trop surcharger les notations. On note la classe de e_(x,y) dans .

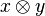
La construction du produit tensoriel permet d'affirmer que est une application bilinéaire, que l'on note .

Montrons que ce module résout bien le problème des applications bilinéaires posé en introduction. Pour cela, donnons-nous une application bilinéaire . Comme le module C est libre, définir une application linéaire de C dans F revient à choisir l'image des éléments de la base canonique de C. On définit ainsi l'application par :

Mais, le fait que f soit bilinéaire implique que :

• 
• 
• 
• 

Donc le sous-module D est inclus dans le noyau de f. On déduit par passage au quotient qu'il existe une application telle que :

De plus g est unique car les éléments de la forme engendrent .

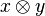
Montrons finalement que est unique à un isomorphisme près, c'est-à-dire que s'il existe un module H tel que :

• Il existe une application bilinéaire surjective .
• Si f : M × N → F est une application bilinéaire, il existe une unique application linéaire g : H → F telle que .

Si tel est le cas, comme est bilinéaire, il existe une application telle que . De même, comme est bilinéaire, il existe une application telle que . Donc et comme est surjectif, on déduit . De même . Donc et H sont des A-modules isomorphes.