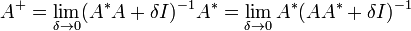Pseudo-inverse - Définition

Introduction

En mathématiques, et plus précisément en algèbre linéaire, la notion de pseudo-inverse (ou inverse généralisé) généralise celle d’inverse d’une application linéaire ou d’une matrice aux cas non inversibles en lui supprimant certaines des propriétés demandées aux inverses, ou en l’étendant aux espaces non algébriques plus larges.

En général, il n’y a pas unicité du pseudo-inverse. Son existence, pour une application linéaire entre espaces de dimension éventuellement infinie, est équivalente à l'existence de supplémentaires du noyau et de l'image. Selon les propriétés demandées, le pseudo-inverse défini permet toutefois de généraliser la notion d'inverse en se restreignant au semi-groupe associatif multiplicatif seul, même s'il ne respecte pas les autres contraintes du corps ou de l'algèbre (en particulier les propriétés de distributivité ou de commutativité ne sont plus vraies dans le cas général, là où le véritable inverse peut les respecter).

En particulier, les types suivants de pseudo-inverses ont été étudiés :

• le pseudo-inverse de Moore-Penrose dans le cas des matrices carrées non inversibles, mais généralisable à toute algèbre de matrices à valeurs dans un corps.
• le pseudo-inverse de Drazin qui détermine la matrice qui constitue un point fixe dans la multiplication par l'exponentiation de matrices carrées au delà d'un degré fini.
• le pseudo-inverse à gauche et le pseudo-inverse à droite, utiles dans le cas des matrices non carrées qui ne sont jamais inversibles pour déterminer la factorisation en valeurs singulières, et qui ne sont pas nécessairement égaux non plus dans le cas de transformées non commutatives comme les opérateurs fonctionnels et distributions non discrètes.

Le pseudo-inverse se calcule à l’aide d’une généralisation du théorème spectral aux matrices non-carrées.

Il est notamment utile dans le calcul de régressions (méthode des moindres carrés) pour un système d'équations linéaires.

Pseudo-inverse de Moore-Penrose

Pour une matrice à coefficients réels ou complexes (pas nécessairement carrée), ou pour une application linéaire entre espaces euclidiens ou hermitiens, il existe un unique pseudo-inverse satisfaisant certaines conditions supplémentaires et appelé pseudo-inverse de Moore-Penrose (ou simplement « pseudo-inverse »), décrit indépendamment par Moore en 1920 et Roger Penrose en 1955. Erik Ivar Fredholm avait déjà introduit le concept de pseudo-inverse pour un opérateur intégral en 1903.

Cas matriciel

Définition

Étant donné une matrice A à coefficients réels ou complexes avec n lignes et p colonnes, son pseudo-inverse A ⁺ est l'unique matrice à p lignes et n colonnes vérifiant les conditions suivantes :

1.  ;
2.       (A ⁺ est un inverse pour le semi-groupe multiplicatif) ;
3.       (AA ⁺ est une matrice hermitienne) ;
4.       (A ⁺ A est également hermitienne).

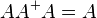
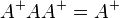
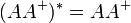
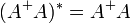
Ici, la notation désigne la matrice adjointe à , c'est-à-dire la transposée pour le cas réel.

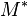
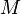
Cette matrice peut s'obtenir comme une limite :

qui existe même si les matrices produits (AA^*) et (A^*A) ne sont pas inversibles.

Propriétés

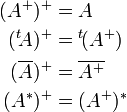
L’opération de pseudo-inversion :

• est involutive ;
• commute avec la transposition et la conjugaison ;

Cependant, la pseudo-inversion n’est pas continue. En effet, elle est inversément linéaire par rapport à la multiplication par un scalaire : pour tout α ≠ 0,

.

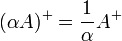
Soit AB est un produit de deux matrices. Si l’une au moins est unitaire, ou si les deux matrices sont de rang maximal égal à leur dimension commune, alors la pseudo-inversion est anti-commutative sur le produit :

.

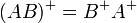
Calcul effectif

Si la matrice A, avec n lignes et p colonnes, est de rang k, alors elle peut s'écrire comme un produit de matrices de même rang A = BC, où B possède n lignes et k colonnes et C possède k lignes et p colonnes. Dans ce cas les produits (CC^*) et (B^*B) sont inversibles et la relation suivante est vérifiée :

.

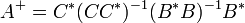
Des approches optimisées existent pour le calcul de pseudoinverses de matrices par blocs.

Algorithmiquement, le pseudo-inverse s'obtient à partir de la décomposition en valeurs singulières : muni de cette décomposition A = UσV ^* , on calcule

A ⁺ = Vσ ⁺ U ^* ,

où σ ⁺ , pseudo-inverse de la matrice diagonale σ, est une matrice diagonale dont les éléments non nuls sont obtenus en inversant les éléments non nuls (de la diagonale) de σ.

À partir d'une matrice dont le pseudo-inverse est connu, il existe des algorithmes spécialisés qui effectuent le calcul plus rapidement pour des matrices en rapport avec la première. En particulier, si la différence n'est que d'une ligne ou colonne changée, supprimée ou ajoutée, des algorithmes itératifs peuvent exploiter cette relation.

Cas particuliers

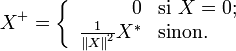
• Le pseudo-inverse d’une matrice nulle est sa transposée (également nulle).
• Le pseudo-inverse d’un vecteur colonne non nul est son vecteur adjoint multiplié par l’inverse de sa norme au carré. En particulier, le pseudo-inverse d’un scalaire (matrice à 1 ligne et 1 colonne) réel ou complexe non nul est son inverse.
• Si le rang de A est égal à son nombre de lignes, la matrice B peut être choisie égale à l’identité et dans ce cas :

  .

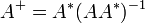
• De même, si le rang de A est égal à son nombre de colonnes,

  .

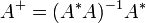
• A fortiori si la matrice A est inversible, son pseudo-inverse est son inverse.
• Si le pseudo-inverse de (A^*A) est connu, on peut en déduire A ⁺ par l’égalité :

   ;

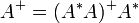
• De même, si (CC^*)⁺ est connu, le pseudo-inverse de A est donné par :

  ;
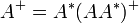