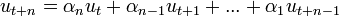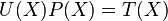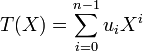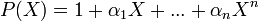Registre à décalage - Définition

Description mathématique

Représentation par les suites

Les suites de bits pouvant être produites par un registre à décalage à rétroaction linéaire sont simples à décrire mathématiquement : ce sont les suites récurrentes linéaires. Autrement dit, on peut obtenir le terme à partir des termes par une équation linéaire du type

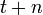
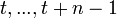
où les valent 0 ou 1.

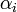
Représentation polynômiale

Il est également possible de les décrire en utilisant les séries formelles :

si à une suite on associe la série alors l'équation ci-dessus peut se mettre sous la forme suivante :

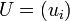
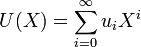
où

Le polynôme correspond à l'initialisation du registre, alors que le polynôme P, appelé polynôme de rétroaction, caractérise le registre.

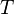
Périodicité

Il est facile de voir qu'une suite produite par un tel registre est nécessairement périodique : le nombre de possibilités combinatoires pour un n-uplet est au plus de 2ⁿ, donc est surjective, soit . Mais, clairement on a et i, . En prenant i = max(t₀ − t₁,t₁ − t₀) on a donc un multiple de la période de la suite.

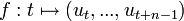
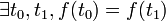
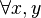
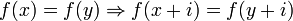
La période maximale est 2ⁿ − 1 car si le n-uplet tout à zéro est atteint, la suite est nécessairement constante égal à zéro. On sait prévoir lorsque cette valeur atteinte, une condition nécessaire et suffisante étant que le polynôme de rétroaction soit primitif -- i.e. est irréductible et tel que, dans l'anneau F₂[X] des polynômes à coefficients binaires, le plus petit t tel que ce polynôme divise X^t − 1 est 2ⁿ − 1 (c'est le polynôme minimal d'un élément d'ordre multiplicatif 2ⁿ − 1 dans le corps à 2ⁿ éléments).

Une suite de période maximale est appelée m-sequence dans la terminologie anglo-saxonne.

Notion de complexité linéaire

Tout m-uplet de bits peut être généré par un LFSR. Plus précisément, il existe toujours un LFSR -- i.e. un polynôme de rétroaction ainsi qu'une initialisation -- tel que les m premières sorties de ce LFSR correspondent au m-uplet. Dans le pire des cas on prend un registre de longueur m, le polynôme de rétroaction important peu dans ces conditions.

Ceci donne lieu à la définition de la complexité linéaire d'une suite (finie) comme la longueur minimale d'un LFSR généré cette suite. Comme le prouve la remarque ci-dessus cette complexité est bornée supérieurement par la longueur de la suite.

Cette notion intervient notamment en cryptographie à cause de l'existence de l'algorithme de Berlekamp-Massey.

Registre à décalage avec rétroaction linéaire

Couramment appelé LFSR, pour Linear Feedback Shift Register en anglais, il s'agit d'une variante avec une unité logique ou arithmétique Le ou les bit(s) en sortie du registre subissent une série d'opérations et de transformations pour être réinsérés dans le registre. Ce type de registre est utilisé en cryptographie pour les implantations matérielles de certains algorithmes de chiffrement de flot. On les retrouve aussi dans certains microprocesseurs dédiés au traitement de signal (DSP), en particulier pour le filtrage. Ce type de circuit est aussi utilisé lors de la phase de test des circuits intégrés en permettant la génération automatique d'entrées (vecteurs de tests).

Rétroaction basée sur un XOR entre plusieurs bits

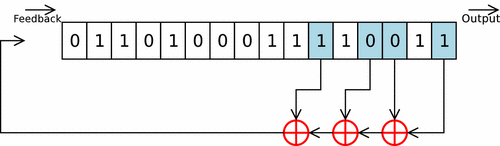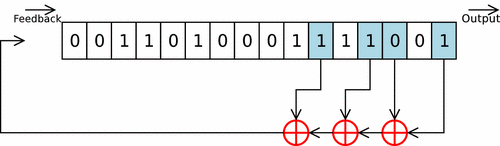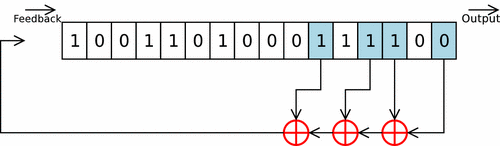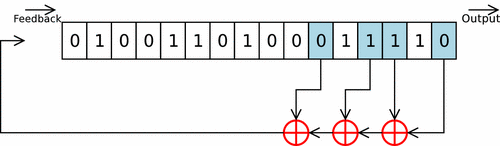
Utilisation

• chiffrement par flot en cryptologie
• division par une puissance de deux (décalage vers la gauche ou la droite)
• tampons pour la réception de données (FIFO : first in - first out)
• compteur, temporisateur