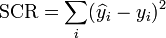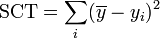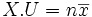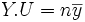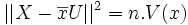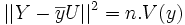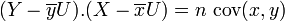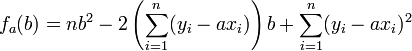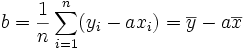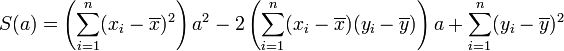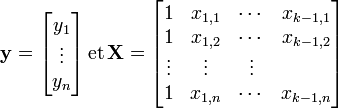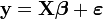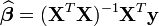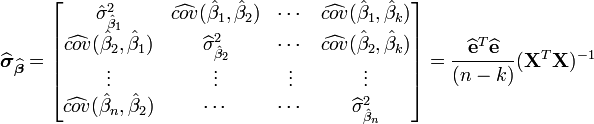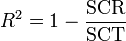Régression linéaire - Définition

Démonstration des formules grâce aux espaces vectoriels de dimension n

Dans l'espace , muni du produit scalaire canonique, on considère le vecteur X de coordonnées (x₁,x₂,...,x_n), le vecteur Y de coordonnées (y₁,y₂,...,y_n), le vecteur U de coordonnées (1, 1, ..., 1).

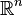
On peut remarquer que :

On note alors le vecteur et le vecteur

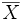
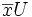
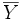
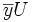
Le vecteur Z de coordonnées (ax₁ + b,ax₂ + b,...,ax_n + b) appartient à l'espace vectoriel engendré par X et U.

La somme représente le carré de la norme du vecteur Y − Z.

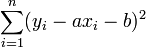
Cette norme est minimale si et seulement si Z est le projeté orthogonal de Y dans l'espace vectoriel vect(X,U).

Z est le projeté de Y dans l'espace vectoriel vect(X,U) si et seulement si (Z − Y).U = 0 et .

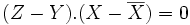
Or donc (Z-Y).U=0 signifie que .

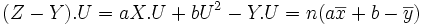
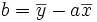
En remplaçant dans , on obtient

donc signifie que

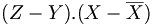
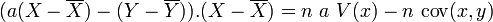
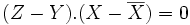
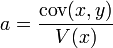
Enfin le coefficient de corrélation linéaire s'écrit alors . Cette quantité représente le cosinus de l'angle formé par les vecteurs et .

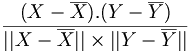
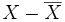
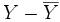
On retrouve alors les résultats suivants:

• si le coefficient de corrélation linéaire est 1 ou -1, les vecteurs et sont colinéaires de coefficient de colinéarité a et . L'ajustement linéaire est parfait.
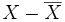
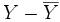
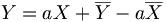
• si le coefficient de corrélation linéaire est en valeur absolue supérieur à alors l'angle formé par les deux vecteurs est compris entre − π / 6 et π / 6 ou entre 5π / 6 et 7π / 6.

Démonstration des formules par étude d'un minimum

1ère étape : détermination de b

Pour tout réel a, on pose . Il suffit de développer et ordonner ce polynôme du second degré en b. On obtient:

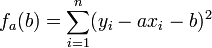
Ce polynôme atteint son minimum en

Ce qui signifie que la droite passe par le point moyen G

Il reste à remplacer dans la somme de départ, b par cette valeur.

2ème étape : détermination de a

Pour tout réel a, . Il suffit de développer et ordonner ce polynôme du second degré en a. On obtient

.

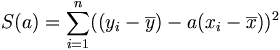
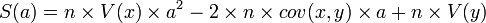
Ce polynôme atteint son minimum en

La droite de régression est bien la droite passant par G et de coefficient directeur .

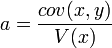
Généralisation: le cas matriciel

Lorsqu'on dispose de plusieurs variables explicatives dans une régression linéaire, il est souhaitable d'avoir recours aux notations matricielles. Si l'on dispose d'un jeu de n données (y_i)_{i = 1..n} que l'on souhaite expliquer par k variables explicatives (y compris la constante) , on peut poser:

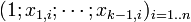
La régression linéaire s'exprime sous forme matricielle:

et il est question d'estimer le vecteur de coefficients k × 1 .

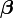
Son estimateur par moindre carré est:

Il faut que la matrice X soit de plein rang ( ) afin que soit inversible.

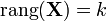
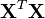
L'estimation de la matrice (symétrique) de variance-covariance de cet estimateur est:

Le terme représente la somme des carrés des résidus ; .

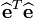
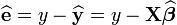
La qualité de l'ajustement linéaire se mesure encore par un coefficient de corrélation R², défini ici par:

où SCR (respectivement SCT) représente la somme des carrés des résidus (respectivement la somme des carrés totaux). Ces sommes s'écrivent et .