Réseau de neurones artificiels - Définition

Modèle

Structure du réseau

Structure d'un neurone artificiel. Le neurone calcule la somme de ses entrées puis cette valeur passe à travers la fonction d'activation pour produire sa sortie.

Un réseau de neurones est en général composé d'une succession de couches dont chacune prend ses entrées sur les sorties de la précédente. Chaque couche (i) est composée de N neurones, prenant leurs entrées sur les N neurones de la couche précédente. À chaque synapse est associée un poids synaptique, de sorte que les N sont multipliés par ce poids, puis additionnés par les neurones de niveau i, ce qui est équivalent à multiplier le vecteur d'entrée par une matrice de transformation. Mettre l'une derrière l'autre les différentes couches d'un réseau de neurones reviendrait à mettre en cascade plusieurs matrices de transformation et pourrait se ramener à une seule matrice, produit des autres, s'il n'y avait à chaque couche, la fonction de sortie qui introduit une non linéarité à chaque étape. Ceci montre l'importance du choix judicieux d'une bonne fonction de sortie : un réseau de neurones dont les sorties seraient linéaires n'aurait aucun intérêt.

Au-delà de cette structure simple, le réseau de neurones peut également contenir des boucles qui en changent radicalement les possibilités mais aussi la complexité. De la même façon que des boucles peuvent transformer une logique combinatoire en logique séquentielle, les boucles dans un réseau de neurones transforment un simple dispositif de reconnaissance d'entrées en une machine complexe capable de toute sortes de comportements.

Fonction de combinaison

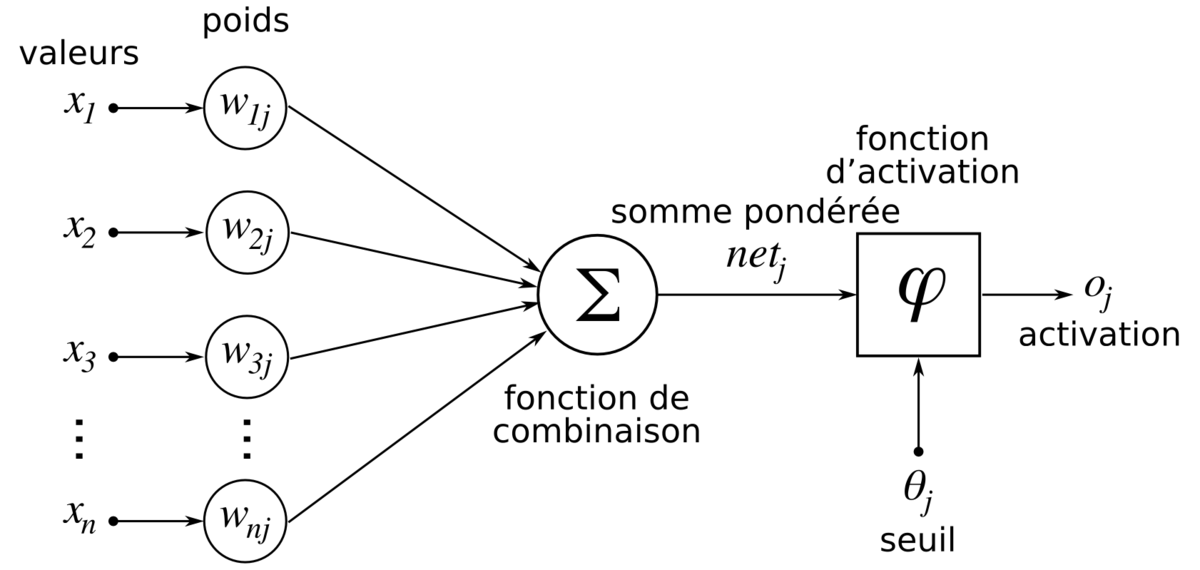
Considérons un neurone quelconque.

Il reçoit des neurones en amont un certain nombre de valeurs via ses connexions synaptiques, et il produit une certaine valeur en utilisant une fonction de combinaison. Cette fonction peut donc être formalisée comme étant une fonction vecteur-à-scalaire, notamment :

• Les réseaux de type MLP (Multi-Layer Perceptron) calculent une combinaison linéaire des entrées, c’est-à-dire que la fonction de combinaison renvoie le produit scalaire entre le vecteur des entrées et le vecteur des poids synaptiques.
• Les réseaux de type RBF (Radial Basis Function) calculent la distance entre les entrées, c’est-à-dire que la fonction de combinaison renvoie la norme euclidienne du vecteur issu de la différence vectorielle entre les vecteurs d’entrées.

Fonction d’activation

La fonction d’activation (ou fonction de seuillage, ou encore fonction de transfert) sert à introduire une non-linéarité dans le fonctionnement du neurone.

Les fonctions de seuillage présentent généralement trois intervalles :

1. en dessous du seuil, le neurone est non-actif (souvent dans ce cas, sa sortie vaut 0 ou -1) ;
2. aux alentours du seuil, une phase de transition ;
3. au-dessus du seuil, le neurone est actif (souvent dans ce cas, sa sortie vaut 1).

Des exemples classiques de fonctions d’activation sont :

1. La fonction sigmoïde.
2. La fonction tangente hyperbolique.
3. La fonction de Heaviside.

La logique bayésienne, dont le théorème de Cox-Jaynes formalise les questions d’apprentissage, fait intervenir aussi une fonction en S qui revient de façon récurrente :

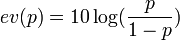
Propagation de l’information

Ce calcul effectué, le neurone propage son nouvel état interne sur son axone. Dans un modèle simple, la fonction neuronale est simplement une fonction de seuillage : elle vaut 1 si la somme pondérée dépasse un certain seuil ; 0 sinon. Dans un modèle plus riche, le neurone fonctionne avec des nombres réels (souvent compris dans l’intervalle [0,1] ou [-1,1]). On dit que le réseau de neurones passe d'un état à un autre lorsque tous ses neurones recalculent en parallèle leur état interne, en fonction de leurs entrées.