Théorème de Cox-Jaynes - Définition

Introduction

Le théorème de Cox-Jaynes (1946) est une codification des processus d'apprentissage à partir d'un certain ensemble de postulats. Cette codification se trouve coïncider au terme de ces considérations avec celle - historiquement d'origine toute différente - de probabilité. Il tient son nom du physicien Richard Cox qui en a formulé la version originale.

Elle induit donc une interprétation « logique » des probabilités indépendante de celle de fréquence. Elle fournit également une base rationnelle au mécanisme d'induction logique, et donc de l'apprentissage par des machines. Qui plus est, le théorème invalide - dans les conditions des postulats - toute autre forme de représentation de la connaissance comme biaisée. Il s'agit donc d'un résultat extrêmement fort. (source : Myron Tribus, Décisions rationnelles dans l'incertain, Masson, 1974)

Les résultats de Cox n'avaient touché qu'une audience réduite avant qu'E.T. Jaynes ne redécouvre ce théorème et n'en défriche une série d'implications pour les méthodes bayésiennes, et Irving John Good pour l'intelligence artificielle.

Problèmes de validité de la démarche inductive avant Cox

Réserves de Bertrand Russell

Dans le chapitre « La science est-elle superstitieuse ? » de son ouvrage Science et religion, Bertrand Russell énonce le problème - il ose même le mot de scandale - posé par l'induction :

• Au nom de quoi affirmer, même de façon provisoire, que ce qui a été vérifié dans un nombre limité de cas se vérifiera aussi dans les cas qui n'ont pas été testés ?
• Au nom de quoi supposer, même sur ce qui a été mesuré, que ce qui a été vrai hier le sera toujours demain ?

Paradoxe de Hempel

Ce paradoxe visait à montrer une faille dans le mécanisme d'induction, qui imposait que le domaine de validité de celui-ci fût précisé de façon plus rigoureuse : le contexte de ce dont on parle doit être toujours mentionné. Ainsi le comptage des oiseaux à la fois non-blancs et non-corbeaux dans une chambre ne renseigne pas sur la probabilité que tous les corbeaux soient blancs, mais que tous les corbeaux soient blancs dans cette chambre - affirmation parfaitement exacte quand il n'y a aucun corbeau dans la chambre, en vertu de la relation (qui définit l'implication)

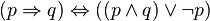
Détails dans l'article Paradoxe de Hempel, dit de l'ornithologie en chambre.

Les règles quantitatives (lois de composition interne)

La règle de somme

Sans rentrer dans les équations, l'idée est que lorsque deux plausibilités du même état se composent, la plausibilité composée est nécessairement égale ou supérieure à la plus grande des deux.

La règle de produit

Il s'agit ici du cas inverse : quand deux plausibilités doivent toutes deux être vérifiées pour qu'un état puisse exister, cet état ne peut avoir de plausibilité plus grande que la plus petite des deux précédentes.

Les « desiderata » (axiomes)

Cox cherche à poser les desiderata souhaitables pour un robot qui raisonnerait selon une logique inductive :

Les degrés de plausibilité sont représentés par des nombres réels

• Il faut bien en effet pouvoir à tout moment dire de deux plausibilités laquelle est plus grande que l'autre, ce qui suggère une représentation quantitative, et la forme numérique semble commode.
• Une représentation entière poserait un problème de bruit discret, aucune plausibilité ne pouvant se glisser entre deux représentées par des entiers successifs.
• Des rationnels conviendraient certes, mais si tous les réels ne sont pas des rationnels, tous les rationnels sont en revanche bien des réels.

La convention adoptée, arbitrairement, est que des plausibilités plus grandes seront représentées par des nombres plus grands.

Les règles d'inférence ne doivent pas contredire les règles d'inférence communes

En d'autres termes, ce qui nous paraît évident ne doit pas être contredit par le modèle (à la différence de ce qui se passe avec le paradoxe de Condorcet).

Exemple :

• si A est préférable à B,
• et B préférable à C,
• toutes choses égales par ailleurs et en l'absence de B, A doit être préféré à C.

Pour les cinq sections suivantes, toutes les formules sont ici :

• Cox-Jaynes (PDF)

Règle de cohérence

Si une conclusion peut être obtenue par plus d'un moyen, alors tous ces moyens doivent bien donner le même résultat.

Cette règle élimine du champ d'examen les heuristiques multiples dès lors qu'elles pourraient contenir entre elles des contradictions (comme le font par exemple parfois les critères de Wald et du minimax en théorie des jeux).

Règle d'honnêteté

Le robot doit toujours prendre en compte la totalité de l'information qui lui est fournie. Il ne doit pas en ignorer délibérément une partie et fonder ses conclusions sur le reste. En d'autres termes, le robot doit être totalement non idéologique, neutre de point de vue.

Règle de reproductibilité

Le robot représente des états de connaissance équivalents par des plausibilités équivalentes. Si deux problèmes sont identiques à un simple étiquetage de propositions près, le robot doit assigner les mêmes plausibilités dans les deux cas.

Cela signifie en particulier que des propositions seront considérées a priori comme de plausibilité équivalente quand elles ne se distinguent que par leur nom - ce qui n'arrive guère que dans des cas très particuliers, comme une pièce ou un dé ayant satisfait à des critères de non-pipage.