Statique du solide - Définition

Statique du solide dans les problèmes à 3 dimensions

C'est par exemple, le cas d'un arbre participant à un engrenage à denture hélicoïdale, un système de renvoi d'angle, ou pourquoi pas un pédalier de bicyclette quand on s'intéresse aux conséquences de pédales trop écartées.

Formalisme des torseurs

Le torseur propose une écriture globale et unifiée des efforts (forces et moments) qui s'exercent sur un système (généralement un solide). De tels torseurs sont généralement nommés torseurs des efforts. Ce formalisme est certes lourd à manipuler à la main et gourmand en papier, mais il permet la résolution systématique de problèmes de mécanique statique et se prête bien à la modélisation et au traitement informatique. De par sa forme analytique, il autorise surtout une modélisation paramétrée d'un problème, ce qui donne accès par exemple à toutes les positions d'un mécanisme, contrairement à l'étude graphique plus rapide, mais qui doit être refaite pour chaque cas et qui est beaucoup moins précise.

Une force est parfaitement définie quand on connaît le vecteur force (appelée aussi résultante) et le point d'application (où son moment s'annule). La notion d'effort, en particulier les efforts de liaison, est bien plus large, et le torseur permet la description de tous les cas.

Le torseur d'action mécanique

Le torseur d'effort, dans sa forme développée donne ces éléments de réduction à savoir :

• la résultante sans précision de point d'application. C'est la somme vectorielle des actions élémentaires de contact ou à distance.
• le moment par rapport à un point arbitrairement choisi. C'est la somme vectorielle des moments des forces élémentaires de contact ou à distance. Sauf cas particuliers, le moment du torseur n'est pas le moment de la résultante (par exemple le torseur couple possède une résultante nulle et un moment non nul). C'est sur cette nuance que reposent les principales difficultés de la modélisation d'efforts par les torseurs.

Il faut considérer 3 niveaux d'écriture de torseur :

• écriture globale: sans distinction de point; Le torseur est l'association de 2 champs de vecteurs sur l'espace (tous les points). La relation de Varignon est donc "intégrée" à cette notation. On n'utilise cette notation qu'au moment du bilan des actions mécaniques ou dans le cadre d'explicitation de réaction.
• éléments de réduction: force ou résultante et moment exprimé en un point (arbitrairement choisi). On utilisera cette forme pour définir en préambule la disposition particulière des actions mécaniques. Il est possible d'effectuer la somme de torseurs à ce niveau. Les moments de tous les torseurs doivent alors être exprimés au même point.
• composantes des éléments de réduction explicitées dans une même base, avec point particulier pour le moment. Présenté sous forme de matrice (souvent 3 lignes, 2 colonnes), cet outil permet d'effectuer simultanément les sommes de forces et de moments (exprimés au même point). Ces composantes sont autant d'inconnues pour les équations à résoudre.

(1->S) en M :

Exemples d'actions mécaniques représentées par des torseurs

• Force appliquée sur S au point A dans la direction x:(F->S) (même forme en tout point de la droite d'action):

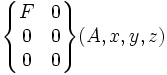
• Couple autour de la direction x:(C->S) en TOUT POINT M :

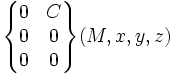
• Liaison ponctuelle en A suivant Y:(1->S) en A :

• Liaison pivot d'axe (B,x):(1->S) (même forme en tout point de l'axe) :

• Torseur de cohésion à l'abscisse x d'une poutre (action du tronçon[x,L] sur le tronçon[0,x])

en G(x) :

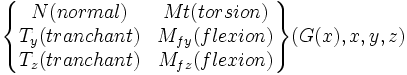
Ce torseur effort représente les efforts transmis à travers la section S(x) d'une poutre. Il est calculable en isolant la partie amont (tronçon[0,x]). Il est toujours défini au centre d'inertie G(x) de la section considérée S(x). Artifice de calcul utilisé en résistance des matériaux. Ainsi les efforts subis à l'intérieur de la pièce deviennent extérieur pour le tronçon isolé, permettant l'application du principe de la statique.

Résolution de problème de statique 3D

Avec le formalisme des torseurs, le principe fondamental de la statique (PFS) s'exprime de la manière suivante

Si un système matériel est en équilibre sous l'effet d'actions mécaniques modélisées par les torseurs  ;  ; …, alors la somme de ces torseurs est égale au torseur nul.

Soit

Attention ! La réciproque (somme des torseurs nulle équilibre) est vraie pour les solides mais pas forcément pour les systèmes déformables. Dans beaucoup d'ouvrages, le principe fondamental de la statique est écrit à l'envers.

Cette relation se généralise en dynamique, en définissant un torseur dynamique qui réunit, sur le même principe, l'accélération et le moment dynamique d'un solide dans un même objet mathématique. Les lois du mouvement de Newton permettent alors d'écrire les relations qui relient le torseur dynamique aux torseur des efforts extérieurs.

Écrit dans la forme la plus développée, l'équilibre du système donne 6 équations dont les inconnues sont les composantes de chaque torseurs d'actions extérieures.

Méthode de résolution d'un problème de statique avec l'outil torseur

La résolution d'un problème de statique ne diffère pas beaucoup des autres méthodes.

1. Inventaire des actions extérieures: chaque action est définie par ses éléments de réduction avec toutes les propriétés particulières explicitement écrites (directions, point particulier...)
2. Transports des moments: C'est l'étape la plus délicate surtout si le problème est complexe. Il faut choisir un point qui permette l'écriture la moins compliquée pour les moments. Ceci dit, n'importe quel point fait l'affaire. L'expérience est seule conseillère en la matière. Dans le cas d'un problème classique, on choisira le point de définition du torseur de liaison le plus complet, ou un point de concours d'axes de liaisons.
3. Équations d'équilibre: les 6 équations (pour un système isolé) alors données par le principe fondamental de la statique peuvent être posées. Il en résulte un système d'équations dont les inconnues sont:

• certaines actions extérieures (celles qu'on veut déterminer).
• les composantes transmissibles dans les liaisons .

Pour de nombreux problèmes, il est souvent nécessaire d'isoler plusieurs systèmes ce qui multiplie le nombre d'équations disponibles, mais aussi le nombre d'inconnues.

Théorème de la résultante (3 équations)

Théorème du moment (3 équations)

Rappel: tous les moments étant exprimés au même point.

Résolution du système d'équations

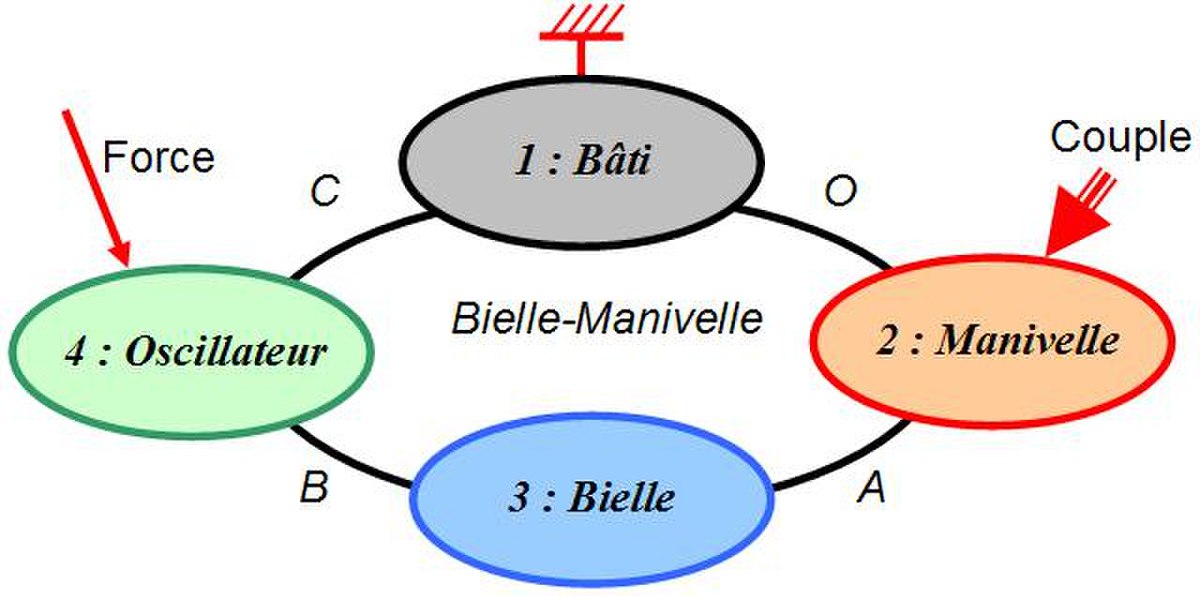
Un problème de statique disposera au mieux d'un nombre d'équations égale à 6 fois le nombre de pièces. Malheureusement, l'isolement d'un seul ensemble d'un mécanisme ne suffit généralement pas, le nombre d'inconnues de liaisons étant facilement supérieur à 6. Il faut donc choisir d'autres sous systèmes afin d'obtenir de nouvelles équations d'équilibre (au risque d'ajouter de nouvelles inconnues de liaison); il n'est pas rare d'avoir à résoudre un système à 18 voire 24 équations sur un mécanisme simple. Le graphe des efforts est un outil d'aide à la décision du choix des systèmes mécaniques à isoler pour obtenir le système le moins coûteux en calcul.

Sur l'exemple ci-contre, l'étude de l'équilibre de la manivelle permet d'établir la relation entre le couple extérieur et les actions de liaison (6 équations). Ensuite l'"isolement" de l'ensemble {bielle+oscillateur} permettra (peut-être) le rapprochement avec F (soit 12 équations). En réalité il faudra aussi isoler la bielle (18 équations en tout). De plus ce problème peut comporter plus d'inconnues que d'équations, et un premier travail consistera à éliminer des inconnues de liaison par des considérations de jeu dans les liaisons. L'étude statique des mécanismes relève donc de la compétence du constructeur en mécanique qui mêlant à la fois connaissances technologiques et physiques.

Cependant dans de nombreux problèmes (isostatiques), on voit apparaître deux systèmes d'équations indépendants :

• une partie concerne la relation entrée/sortie qui lie les actions motrice et réceptrice (souvent une seule équation). Cette partie concerne les efforts fournissant une puissance.
• le reste peut s'appeler équations de liaisons qui renseignent sur les efforts (auparavant transmissibles et désormais effectifs) de guidage et qui s'expriment en fonction des efforts précédents. La puissance de ces interactions est nulle si les liaisons sont parfaites.

Selon les besoins, il n'est pas nécessaire de résoudre l'ensemble des équations. La méthode dite des puissances virtuelles permet de séparer mathématiquement ces deux groupes d'inconnues.

Dans le cas des systèmes hyperstatiques, le nombre d'équations demeure insuffisant. Alors, on a recours à l'élimination d'inconnue par des considération de jeu dans les liaisons, ou alors à l'écriture de nouvelles équations en posant l'étude du comportement élastique de certaines pièces.