Statique du solide - Définition

Introduction

La statique du solide est la branche de la statique étudiant l'équilibre des pièces dans un mécanisme. C'est un maillon essentiel dans le dimensionnement des systèmes mécaniques réels.

Statique du point et statique du solide

Les simplifications de la mécanique du point reposent sur le fait que le point est invariant par rotation, et que toutes les forces sont appliquées au point matériel. Alors les forces suffisent à modifier sa position. Pour les solides, constitués d'une infinité de points matériels, les déplacements possibles, appelés aussi degrés de liberté, sont de deux natures: translations (3 directions principales) et rotations (autour de ces trois directions). Alors que les translations ne peuvent être provoquées que par des forces, les rotations sont générées par des moments de ces forces, ou autres couples de force.

Quand l'équilibre d'un point ne nécessite l'établissement que de 3 relations algébriques (équation vectorielle des forces à 3 dimensions), celui du solide demande alors la considération de 3 équations supplémentaires (équation vectorielle des moments).

Le principe fondamental de la statique se compose alors :

1. du théorème de la résultante (somme des forces nulle).
2. du théorème du moment (somme des moments nulle).

L'étude de l'équilibre d'un solide nécessite toujours la considération de ces 2 théorèmes, même si certains cas simples, traités en mécanique du point, semblent être résolus avec une seule des 2 parties. En règle générale, il n'est pas possible de traiter séparément les deux aspects (forces et moments): il s'agit bien d'un problème complexe à 6 dimensions.

D'autre part, la statique du solide, et plus généralement des mécanismes, prend en considération les efforts transmissibles dans une liaison mécanique. L'étude de ces liaisons donne a priori et sans équivoque certaines caractéristiques des forces et moments des actions entre solides. L'objectif étant la détermination complète de tous ces efforts inconnus.

Cas des liaisons mécaniques avec frottement

Le frottement a une influence sur le comportement statique des liaisons mécaniques. Certains modèles comme les lois de Coulomb décrivent ce comportement. De ce fait, même si cela complique le problème, non seulement ça n'induit pas d'inconnue statique supplémentaire, mais dans certains cas, cela en diminue le nombre.

Enfin la considération du frottement est parfois obligatoire pour la résolution d'un problème, comme par exemple l'équilibre d'une échelle, ou le dimensionnement d'un embrayage.

Statique du solide dans les problèmes plans

Modélisation

Degrés de liberté

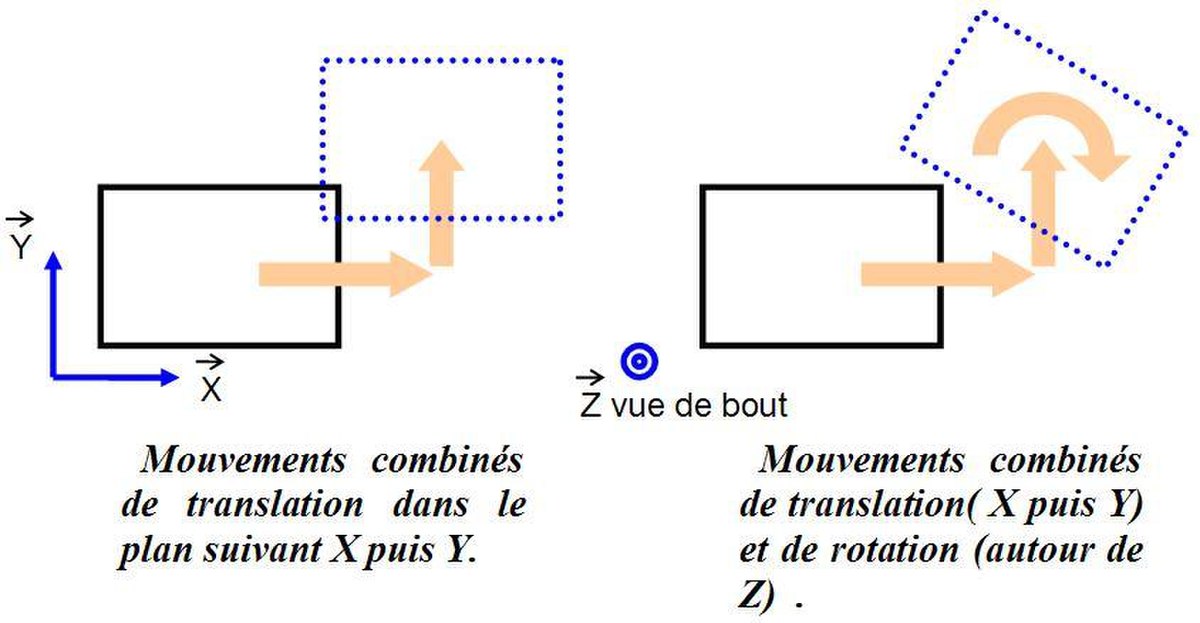
Dans de nombreux problèmes les forces impliquées sont coplanaires. C’est-à-dire qu'il existe un plan vectoriel (x,y) dans lequel on peut observer ces forces en vraie grandeur. Dans ce cas les solides étudiés sont aussi considérés prisonniers de ce plan: leurs degrés de liberté sont au nombre de 3 :

• translation suivant la direction x
• translation suivant la direction y
• rotation autour de la direction z

C'est par exemple le cas du système bielle-manivelle en vue de bout de manivelle, du train que la vache regarde passer, du mécanisme d'une montre, etc.

Efforts transmissibles

Dans ce cadre, les seuls efforts à considérer sont :

• les forces dans le plan (x,y)
• les moments autour de z. Ce qui autorise une représentation scalaire du moment d'une force.

L'objectif de la mécanique est la détermination de tous les efforts appliqués à un système, à partir de la connaissance d'une partie d'entre eux. En ce qui concerne les mécanismes, il s'agit en plus de connaître les charges subies dans toutes les liaisons. Le mécanicien n'a a priori aucune information sur la disposition réelle de ces efforts. Cependant, pour chaque liaison, dont on connait le comportement, certaines composantes (forces ou moments) sont nulles ou au contraire transmissibles. C'est ainsi qu'on peut dire que la réaction d'un support plan sur un pavé est une force obligatoirement perpendiculaire au contact s'il n'y a pas de frottement. Lorsque l'étude est terminée, on peut décrire chaque effort de liaison qui devient alors l'effort effectivement transmis.

Liaisons mécaniques

Sous l'hypothèse de problème plan, les 10 liaisons mécaniques élémentaires étant affectées d'une suppression de degrés de liberté, ne sont plus que 3 :

• la liaison ponctuelle qui supprime une translation.
• le pivot (ou articulation) qui supprime les deux translations.
• la glissière qui ne laisse qu'une translation.

Si elles sont parfaites, alors nous disposons d'informations supplémentaires sur les efforts transmissibles dans ces liaisons, à savoir :

• ponctuelle: point d'application et droite d'action connus; intensité dépendant des autres efforts.
• pivot: droite d'action passant nécessairement par le centre. Intensité et direction à déterminer.
• glissière: direction connue (perpendiculaire à la translation autorisée). Intensité et point d'application à déterminer.

Ces données sont à inscrire dans le bilan des forces extérieures à un solide. L'étude aboutira à l'identification de toutes les forces effectivement transmises (incluses dans l'ensemble des forces transmissibles) à savoir, pour chaque force, son point d'application, sa droite d'action, son sens et son intensité.

Méthode graphique

Pour ces problèmes la résolution par méthode graphique s'avère à la fois plus rapide, souvent bien plus simple, et finalement très précise (moins de 5% d'erreur par rapport à la résolution analytique). La résolution analytique de tels problèmes repose sur une exploitation de la géométrie et la manipulation d'outils mathématiques plus complexes; seulement, à partir de l'étude d'une seule position, on peut espérer écrire une loi générale sur l'ensemble des positions. Les logiciels de calcul donnent évidemment tous ces résultats instantanément; faut-il encore saisir le modèle: aujourd'hui avec les outils de CAO, le même modèle est utilisé pour la conception, les calculs, les mises en plan, le prototypage, etc.

Les paragraphes suivants sont écrits dans cette hypothèse de problème plan.

Dans ce contexte, les efforts inconnus (ou connus) sont représentés par des vecteurs force appliquée en un point. Ce qui amène à considérer pour chaque cas :

• un point d'application
• une direction (donc une droite d'action)
• une intensité (orientée sur la droite d'action)

L'étude n'est terminée que si ces trois items (point, droite et vecteur) sont définis pour chaque force. Quelques rares cas ne demanderont pas une étude complète. Parfois le problème comprend un effort de type couple ; alors la résolution est partiellement analytique.

Moments et couples de forces

Sous l'hypothèse de problème plan, l'expression du moment peut être modifiée. On ne considère plus les rotations autour d'un axe mais seulement dans la direction Z soit en fait autour d'un point (c’est-à-dire autour d'un axe de direction Z passant par le point considéré). Une seule composante étant non nulle, la représentation vectorielle devient scalaire.

Moment d'une force

L'équilibre d'un solide signifie qu'il ne bouge pas (dans un référentiel donné) soit :

• aucune translation
• aucune rotation autour de quelque point (ou pivôt) que ce soit.

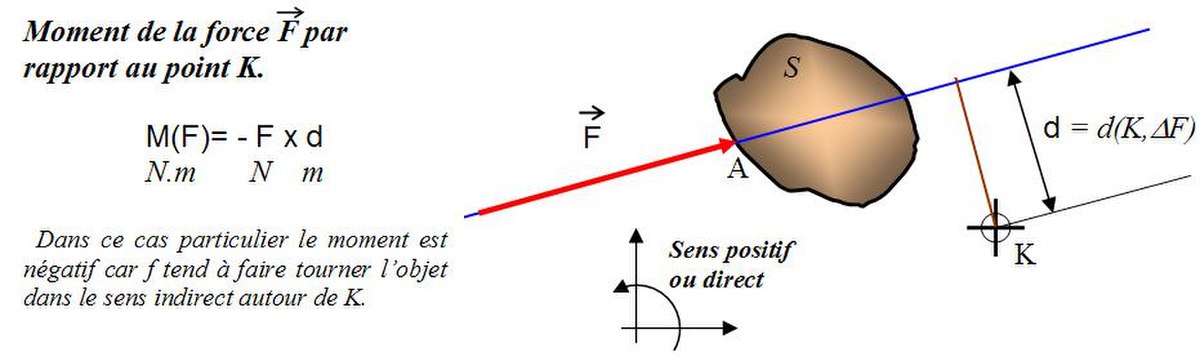
On peut alors considérer la capacité d'une force à faire tourner le solide autour d'un point donné. Cette grandeur est appelée moment de force. Il n'y a pas nécessité de pivot réel. Ce moment dépend de plusieurs facteurs : l'intensité de la force, les positions relatives de la force et du point.

M(F)= +/- d.F (en N.m) où d bras de levier, est la distance (minimale) entre le point et la droite d'action de la force. le signe est apprécié suivant que la force tend à faire tourner dans le sens direct (x vers y) ou indirect (y vers x). Avec d'autres modèles tels que le torseur, le choix du signe ne se pose pas; il est directement déduit des calculs, et son sens est lié à l'orientation de l'espace (trièdre direct).

Il est intéressant de voir à présent les cas de nullité du moment d'une force. De l'équation ci-dessus, on en déduit aisément deux :

• La force est nulle. Sans intérêt puisqu'il n'y plus de force.
• la distance d est nulle : ce qui signifie que le point de pivot se trouve sur la droite d'action. Cette propriété géométrique sera exploitée par la suite.

Couple de forces

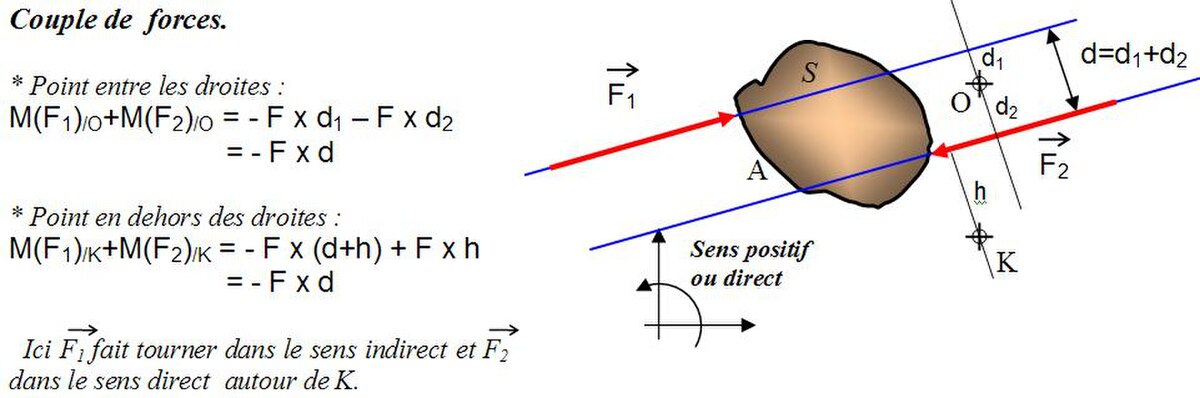
Si 2 forces opposées (donc de même intensité), s'appliquent sur un même corps suivant deux droites d'action distinctes (donc strictement parallèles) et distantes de d, on imagine sans mal que ces forces se compensent, cependant l'équilibre du corps semble ne pas être assuré. Cette disposition est appelée couple de forces. Pour vérifier cela, en appliquant la méthode vue ci-dessus, calculons la somme des moments de ces 2 forces, en différents points de l'espace.

Dans tous les cas cette somme a une même valeur C = - d.F . On appelle couple cette valeur indépendante du point de pivot considéré. Derrière l'appellation couple, les forces disparaissent (puisque elles se compensent). En réalité, dans la nature, un couple (sans forces pour le générer) n'existe pas. L'intérêt du couple est cette résultante nulle. Chacun aura fait l'expérience de desserrer une roue de voiture avec une manivelle (force unique et moment de force par rapport à l'axe de la vis) qui ripe facilement, ou avec une croix (2 forces opposées qui forment un couple) assurant non seulement une plus grande intensité de desserrage mais aussi une meilleure stabilité de l'outil. Dans un moteur électrique, le bobinage est tel qu'il existe toujours deux "bouts de fil" symétriquement disposés par rapport à l'axe de rotation et parcourus par des courants induisant deux forces de Laplace opposées, soit un couple élémentaire.

Plus généralement un couple est la somme non nulle de moments de forces dont la résultante s'annule. Pour la suite, chaque couple annoncé ne fera plus apparaître les forces qui le génèrent.

Étude de cas et résolutions

Cas d'équilibre à 2 forces

Ce cas élémentaire permet de montrer comment un problème de statique ne dissocie pas forces et moments. Non seulement l'étude permet la détermination de l'ensemble des forces, mais aussi les conditions géométriques de l'équilibre. Pour cette étude de cas, comme pour les suivantes, le principe fondamental de la statique nous donne les relations suivantes :

• aucun mouvement de translation possible: somme des forces extérieures nulle.
• aucun mouvement de rotation possible: somme des moments des forces extérieures nulle (moments calculés en un même point qui peut être choisi arbitrairement).

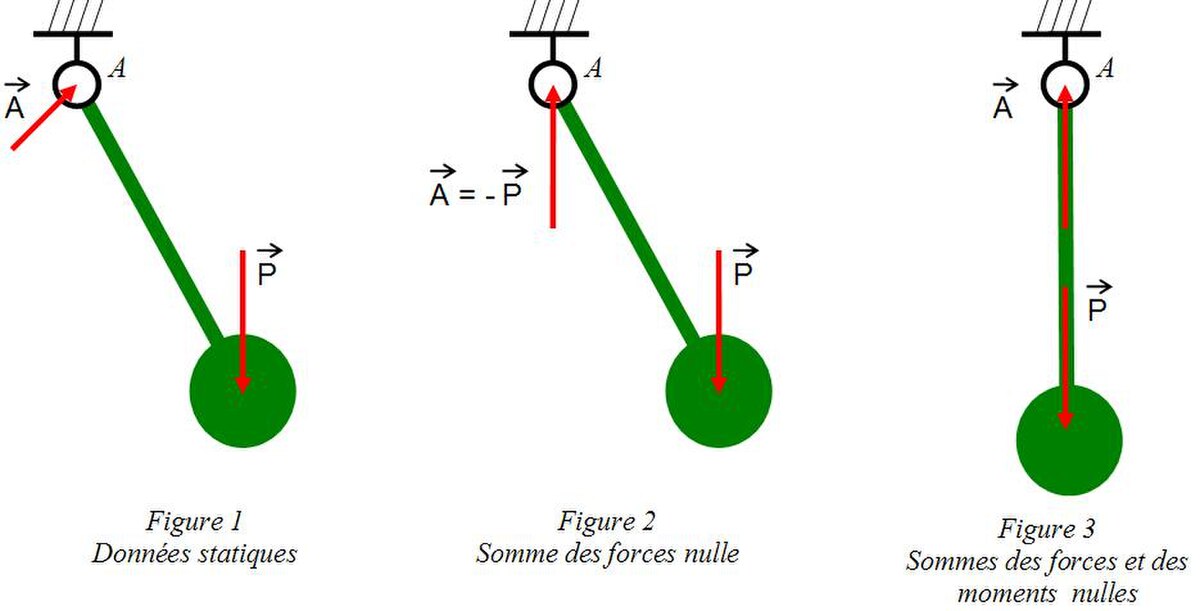
Soit l'étude d'un pendule: la figure 1 ci-dessous donne une position quelconque. L'objectif est la détermination des conditions d'équilibre. le bilan des actions extérieures nous donne :

• le poids appliqué au centre de gravité de valeur connue.
• le pivot (ou articulation) parfait en A. la droite d'action passe par l'axe, mais est de direction inconnue.

L'équation d'équilibre relative aux forces donne donc: Ce qui définit l'action dans le pivot de façon univoque, les deux forces formant alors un couple. La position proposée (figure 2) n'est donc pas une position d'équilibre.

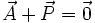
L'équation des moments, par exemple calculée au point A, nous donne: soit

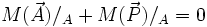
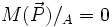
Ce qui revient à dire que A appartient à la droite d'action du poids. Nous aurions abouti à la même conclusion, peut être plus difficilement, en calculant les moments en n'importe quel point. En règle générale, le point de calcul des moments doit être choisi sur un critère de simplicité de calcul. Ici A ou G (centre de gravité) assurent l'annulation d'un des moments de force.

De ce fait les seules positions d'équilibre sont celles ou le pendule est vertical, en dessous (position stable) ou au-dessus de l'axe (position instable).

En résumé : pour qu'un solide soumis à deux forces soit en équilibre:

• les deux forces sont opposées (équation vectorielle des forces)
• même droite d'action pour les deux forces (équation du moment)

Pour la résolution graphique d'un problème de statique ces conditions géométriques sont équivalentes à l'énoncé du principe fondamental de la statique.

Cas d'équilibre à 3 forces

C'est certainement le cas le plus fréquent dans les mécanismes peu hyperstatiques. Comme dans l'étude précédente, l'application simultanée des 2 théorèmes permet de déterminer à la fois les forces mais aussi leur disposition.

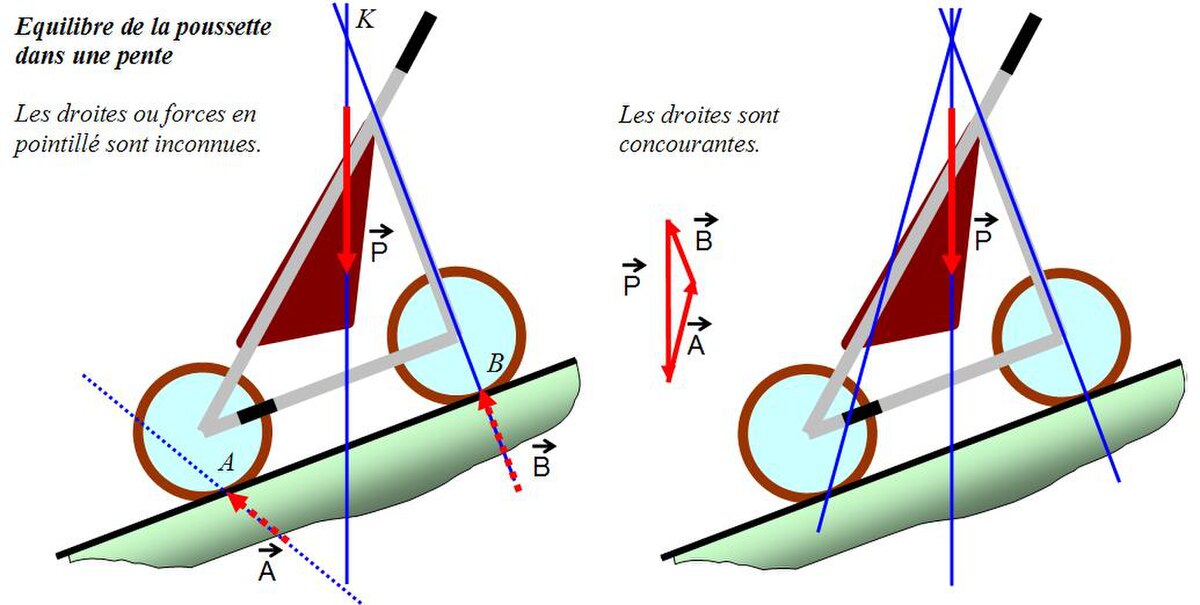
Considérons le cas de la poussette maintenue dans une descente par le seul frein sur la roue avant, la roue arrière étant libre. Seul le poids de la poussette est connu.

Un premier bilan des actions extérieures fait état de :

• poids appliqué au centre de masse G. Donné.
• l'action du sol sur la roue avant, appliquée au point A.Direction inconnue.
• l'action du sol sur la roue arrière, appliquée au point B. Une étude préliminaire (équilibre de la roue arrière seule) montrerait (cas précédent d'un solide sousmis à 2 forces) que cette action est forcément perpendiculaire au sol (y compris avec la considération de frottement au contact du sol et à condition que le pivot de roue soit parfait).

Il semble difficile d'établir la somme nulle des forces puisque deux d'entre elles sont inconnues. Toutefois on peut écrire : . Géométriquement cela se traduit par la construction d'un triangle fermé, dont un seul côté est pour l'instant parfaitement défini.

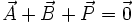
Au moins deux droites d'action sont ici connues: celles de l'action en B et du poids. Elle concourent en un point qu'on notera K. Leurs moments respectifs en K sont donc nuls. Si on applique le théorème en ce point K, on obtient :

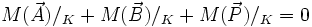
soit d'où

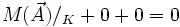
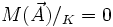
Nécessairement K appartient à la droite d'action en A. Ce qui revient à dire que les trois droites sont concourantes en K. On connait désormais la direction de la droite d'action en A.

Revenons à la première équation; il est possible alors de construire le triangle. En traçant en premier le poids connu, on reporte à chaque extrémité une droite respectivement parallèle aux droites des deux autres actions. Le triangle se forme alors et le relevé des longueurs des côtés donne le résultat. Cette méthode impose même le sens des actions mécaniques. Il resterait à vérifier que l'action en A satisfait les lois de Coulomb sur le frottement pour valider l'équilibre.

En résumé : pour un système soumis à 3 forces extérieures, dont 2 concourantes :

• les vecteurs force forment un triangle fermé (équation des forces)
• toutes les droites d'action sont concourantes.

Si les deux droites connues n'avaient pas été concourantes, alors elles auraient été parallèles. Ce qui revient au cas du levier donné plus haut. Dans le cas de force parallèle un calcul est nécessaire (relatif à l'écriture des moments) pour déterminer une relation entre les intensités des forces.

Cas d'équilibre à 2 forces et un couple

Si un solide est soumis à deux forces (de point et droites d'actions distincts), et un couple de force (donc action de force résultante nulle), de l'équilibre selon le principe fondamental de la statique découlent les conséquences suivantes :

• les deux forces sont opposées et constituent donc un couple de forces.
• les deux couples de forces s'annulent.

Par exemple, une dynamo actionnée par une manivelle: les bobinages induisent un couple dont l'intensité est en rapport avec le courant électrique généré. L'action sur la manivelle, qui dans le cas le plus favorable, est circonférentielle (tangente au cercle décrit par la main). Enfin, la manivelle est liée au bâti par un guidage suivant un liaison pivot dont la force transmissible est appliquée sur l'axe. De la première relation on déduit la direction de l'action du palier, qui tourne avec la main; de la deuxième on établit alors la relation entre l'action du pousseur et le couple d'origine électrique.