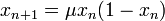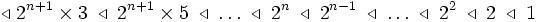Suite logistique - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, une suite logistique est un exemple simple de suite dont la récurrence n'est pas linéaire. Souvent citée comme exemple de la complexité pouvant surgir de simple relation non linéaire, cette suite fut popularisée par le biologiste Robert May en 1976.
Sa relation de récurrence est
Elle conduit, suivant les valeurs de μ, à une suite convergente, une suite soumise à oscillations ou une suite chaotique.
Elle est la solution en temps discret du modèle de Verhulst. Le terme « logistique » provient de l'ouvrage de Pierre François Verhulst qui appelle courbe logistique la solution en temps continu de son modèle. Il écrit en 1845 dans son ouvrage consacré à ce phénomène : « Nous donnerons le terme de logistique à cette courbe ». L'auteur n'explique pas son choix mais « logistique » a même racine que logarithme et logistikos signifie « calcul » en grec.
Comportement selon µ
Dans le modèle logistique, la variable notée ici xn désigne l’effectif de la population d'une espèce. En faisant varier le paramètre µ, plusieurs comportements différents sont observés :
- Si 0≤µ≤1, l’espèce finira par mourir, quelle que soit la population de départ. Autrement dit,
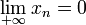
- Si 1≤µ≤2, la population finit par se stabiliser autour de la valeur
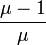
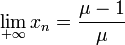
- Si 2≤µ≤3, elle finit également par se stabiliser autour de
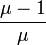
- Si 3<µ≤1+√6 (environ 3,45), elle finit par osciller entre deux valeurs, dépendantes de µ, mais pas de la population initiale.
- Si 3,45<µ<3,54 (environ), elle finit par osciller entre quatre valeurs, là encore dépendantes de µ mais pas de la population initiale.
- Si µ est légèrement plus grand que 3,54, la population finit par osciller entre huit valeurs, puis 16, 32, etc. L’intervalle des valeurs de µ conduisant au même nombre d’oscillations décroît rapidement. Le rapport entre deux de ces intervalles consécutifs se rapproche à chaque fois de la constante de Feigenbaum, δ = 4,669…. Aucun de ces comportements ne dépend de la population initiale
- Vers µ = 3,57, le chaos s’installe. Aucune oscillation n’est encore visible et de légères variations de la population initiale conduisent à des résultats radicalement différents.
- La plupart des valeurs au-delà de 3,57 présentent un caractère chaotique, mais il existe quelques valeurs isolées de µ avec un comportement qui ne l’est pas. Par exemple vers 3,82, un petit intervalle de valeurs de µ présente une oscillation entre trois valeurs et pour µ légèrement plus grand, entre six valeurs, puis douze, etc. D’autres intervalles offrent des oscillations entre 5 valeurs, etc. Toutes les périodes d’oscillation sont présentes, là encore indépendamment de la population initiale.
- Les périodes d'oscillation précédemment décrites répondent à la règle suivante. Considérons l'ordre de Sarkovskii défini sur les entiers strictement positifs de la façon suivante :
-
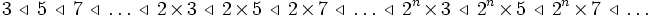
-
- Autrement dit, on place d'abord les impairs à partir de 3 par ordre croissant, puis les impairs multipliés par 2, puis par 4, etc. et on termine par les puissances de 2 par ordre décroissant. Si une valeur du paramètre µ correspond à une période d'oscillation n, alors tous entiers succédant à n dans l'ordre de Sarkovski correspondent à des périodes d'oscillation déjà apparues pour des valeurs du paramètre inférieures à µ. Ainsi, puisque µ = 3,82 correspond à une période 3, toutes les périodes d'oscillation possibles sont déjà apparues pour des valeurs de µ entre 0 et 3,82.
- Au-delà de µ=4, la population quitte l’intervalle [0;1] et diverge quasiment pour toutes les valeurs initiales.
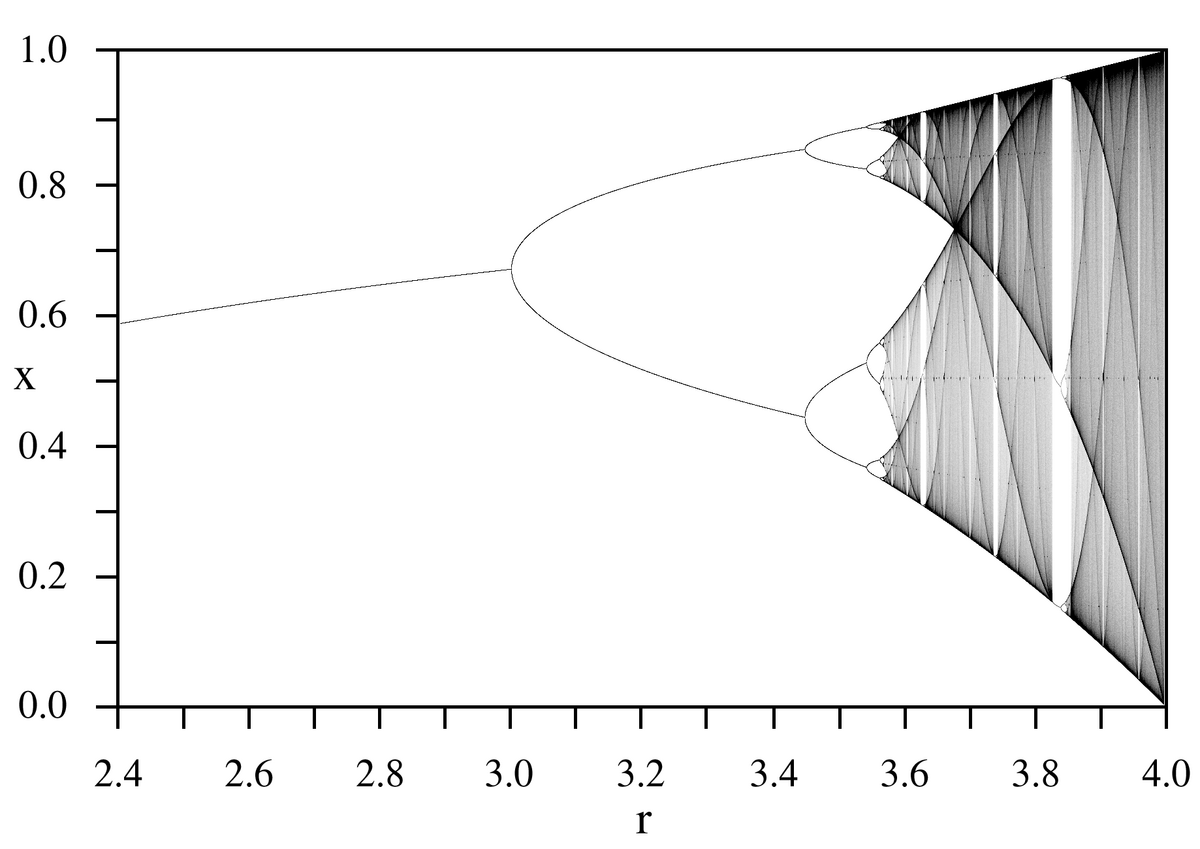
Un diagramme de bifurcation permet de résumer tout cela :