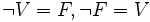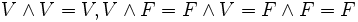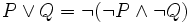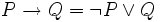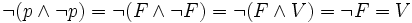Théorème de complétude (calcul des propositions) - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le calcul des propositions est un calcul logique restreint. On emploie souvent le nom de proposition pour désigner une formule logique non quantifiée. Il existe deux façons de valider une formule P du calcul des propositions :
- ou bien on montre que cette formule est vraie dans tout modèle (voir ci-dessous). On dit alors que P est une tautologie, et on note
- ou bien on montre que cette formule est prouvable ou dérivable en utilisant un système de déduction, et on note
Un système de déduction correct doit être construit de façon que, à partir de formules vraies (tautologies), on puisse déduire d'autres formules vraies. Dans ce cas, si
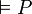
Le système de déduction sera complet, si inversement, il permet de déduire toute formule vraie. Autrement dit, si
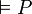
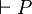
Le théorème de complétude du calcul des propositions énonce que les systèmes de déduction, décrits dans les articles calcul des propositions ou déduction naturelle ou calcul des séquents, sont complets. Il y a équivalence entre être une tautologie et être prouvable.
Le théorème de complétude du calcul des propositions classique a été démontré par Paul Bernays en 1926.
Vérité et fausseté d'une proposition dans un modèle
Pour le calcul des propositions, il n’est pas nécessaire d’analyser la structure des formules atomiques en prédicats et objets. La seule propriété des propositions atomiques qui compte dans les calculs de la logique classique est leur vérité ou leur fausseté. On peut représenter les propositions par des lettres, p, q, r, ... et les concevoir comme des variables qui peuvent recevoir deux valeurs, V pour vrai, et F pour faux.
Un modèle est défini par l’attribution de valeurs de vérité, V ou F, aux propositions atomiques. Par exemple (p = V,q = F,r = V) désigne le modèle
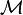
On peut définir un calcul des vérités semblable au calcul des nombres et utilisant les connecteurs logiques non

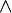
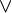
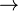
Les règles relatives à
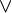
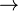
On peut alors calculer, par exemple, que dans le modèle
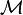
On en conclut que
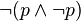
Démonstration du théorème de complétude du calcul des propositions classique
Systèmes de déduction
On peut montrer que les systèmes de déduction cités en préambule permettent en particulier d'effectuer les déductions suivantes :
-
-
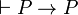
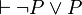
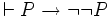
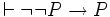
- si
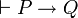
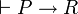
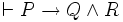
-
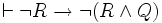
- si
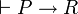
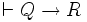
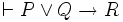
- si
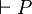
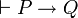
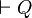
-
Nous allons maintenant démontrer que, dans ces systèmes :
-
- (i) Si une proposition est une tautologie alors elle est dérivable.
Il suffit de montrer le théorème pour des modèles finis. En effet, donnons-nous un ensemble infini dénombrable, ordonné par les entiers positifs, de propositions atomiques, toutes distinctes, p1, p2, p3... Un modèle initial de longueur n contient ou bien pi = V ou bien pi = F, mais pas les deux, pour
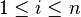
Démonstration d'un résultat liminaire
Pour démontrer (i), on va d’abord démontrer (ii) et (iii) ci-dessous. Soit P une formule propositionnelle, et
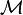
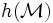
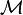
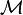
-
- (ii) Si P est vraie dans le modèle
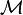
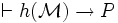
- (ii) Si P est vraie dans le modèle
-
- (iii) Si P est fausse dans le modèle
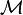
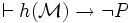
- (iii) Si P est fausse dans le modèle
On va démontrer (ii) par induction sur la complexité des formules. Celle-ci est mesurée par le nombre maximal d’opérateurs emboités. Par exemple dans
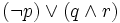
Soit pi une proposition de complexité 0, c’est-à-dire une proposition atomique. La formule
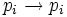
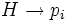
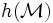
Supposons que (ii) et (iii) soient vraies pour toutes les propositions de complexité au plus égale à n. Soit P une proposition de complexité n + 1. Deux cas sont possibles.
a) il y a un Q tel que
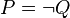
- Si P est vraie dans le modèle
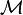
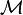
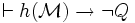
- Si P est fausse dans le modèle
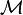
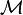
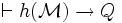
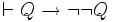
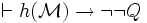
b) il y a R et S tels que
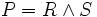
- Si P est vraie dans le modèle
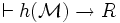
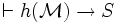
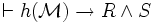
- Si P est fausse dans le modèle
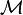
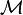
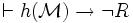
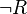
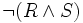
Cela termine cette démonstration de (ii) et (iii).
Fin de la démonstration du théorème de complétude
Prouvons maintenant (i), le théorème de complétude, par induction sur la longueur des modèles. Soit In l’énoncé : Si P est vraie dans tous les modèles de longueur n alors P est dérivable. Démontrons par récurrence les énoncés In.
Prouvons d’abord I1. Supposons que P est vraie dans tous les modèles de longueur 1, c’est-à-dire les deux modèles p1 = V et p1 = F. On a alors, d'après (ii)
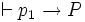
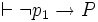
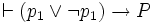
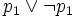
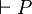
Supposons que In soit vrai. Soit P une proposition vraie dans tous les modèles de longueur n + 1. Soit
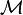
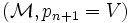
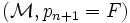
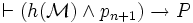
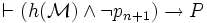
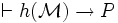
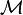
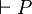
Cela termine cette démonstration du théorème de complétude du calcul des propositions.