Trace (algèbre) - Définition

Exemples

Soit E un espace vectoriel de dimension n.

• La trace de l'identité Id est : Tr(Id) = n = dim E.
• La trace d'une transvection est aussi dim E.
• Pour tous opérateurs u et v, on pose [u,v]=uv-vu. La trace de [u,v] est nulle, ce qui signifie exactement Tr(uv)=Tr(vu).

Dans les espaces euclidiens :

• La trace d'une rotation de R² d'angle θ est donnée par : Tr(R_θ) = 2cosθ.
• Plus généralement pour tout entier , la trace d'une rotation d'axe Δ et d'angle θ dans l'espace à n dimensions est donnée par : Tr(R_Δ,θ) = n − 2 + 2cosθ.

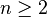
Pour des matrices :

• Toute permutation (où représente le groupe symétrique d'ordre ) est représentée par une matrice carrée d'ordre , définie par :

  

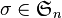
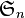
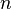
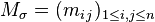
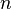
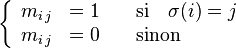
  La trace de la matrice M_σ s'interprète alors comme le nombre de points fixes de la permutation σ :

  

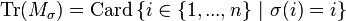
• La trace de la matrice d'adjacence d'un graphe est nulle (si un sommet ne boucle pas sur lui-même).

Généralisations

Opérateurs à trace

En dimension infinie, un espace de Hilbert H est séparable ssi il admet une base orthonormée complète . Un opérateur A est dit à trace si

.

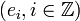
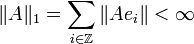
Dans ce cas, on pose

.

Les opérateurs à trace forment un espace vectoriel noté L¹(H), qui est complet pour la norme . La trace définit une forme linéaire continue Tr de L¹(H) vers R.

.

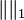
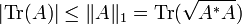
En dimension finie, la trace d'un opérateur est la somme des coefficients diagonaux d'une représentation matricielle. L'exemple suivant en est une généralisation. Soit μ une mesure borélienne sur un espace topologique compact K. Soit une application continue. Sur l'espace de Hilbert des fonctions des fonctions de carré sommable, elle définit l'opérateur à noyau

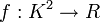
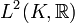
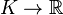
est un opérateur à trace, et sa trace vaut :