Trace (algèbre) - Définition
La liste des auteurs de cet article est disponible ici.
Applications
Réduction d'opérateurs
Un projecteur p de E est un opérateur vérifant p2=p. Le lemme des noyaux implique que E est la somme directe du noyau F de p et de l'image G de p ; et p se restreint en l'identité sur G. Géométriquement, p est la projection sur G parallèlément à F. En concaténant des bases de F et G, on a une base de E dans laquelle le matrice de u est diagonale avec comme coefficients 0 et 1. Il s'en suit que la trace de p est la dimension de G :
-
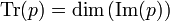
Plus généralement, les traces fournissent des informations sur la réduction des opérateurs. On rappelle que le polynôme caractéristique de u est
- P(X) = det(X − u).
Si P(X) est scindé (par exemple, si le corps de base K est algébriquement clos) alors u est triangularisable. Autrement dit, il existe une base de E dans laquelle l'opérateur u s'écrit sous la forme d'une matrice triangulaire supérieure. Les coefficients diagonaux sont les racines de son polynôme caractéristique P(X) comptées avec multiplicité, qui sont les valeurs propres de u. On les note ici
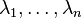
-
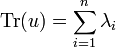
En particulier, le développement du polynôme caractéristique est
-
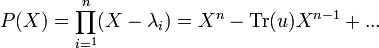
Les autres coefficients du polynôme caractéristique sont les valeurs des polynômes symétriques élémentaires en
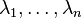
-
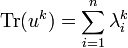
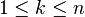
Par exemple, si E est de dimension 3,
-
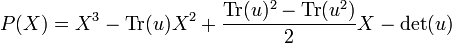
L'application suivante est un exercice proposé au concours d'entrée de l'École polytechnique. Soit u un opérateur sur un espace vectoriel réel E, tel que
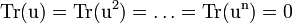
Divergence
Étant donné un espace vectoriel réel E de dimension finie, le déterminant définit une application det de l'espace des opérateurs sur E vers R, qui est homogène de degré n. Le nombre det(u) s'exprime comme une fonction polynômiale en les coefficients de la matrice représentant u dans une base quelconque de E. La fonction det est donc différentiable. Sa différentielle en l'identité est la trace. Autrement dit, pour tout opérateur u sur E,
- det(I + u) = 1 + Tr(u) + o(u)
où o(u) signifie que le reste est négligeable devant u quand u tend vers zéro. Comme conséquence, pour tout opérateur u sur E,
- det(exp(u)) = exp(Tr(u)).
En particulier, l'exponentielle de u est de déterminant 1 ssi u est un opérateur de trace nulle. Ce résultat s'interprète dans la théorie des groupes de Lie comme suit. L'application det est un morphisme continu de groupes du groupe linéaire GL(E) vers R. Son noyau, l'ensemble des opérateurs de déterminant 1, donc est un sous-groupe de GL(E), noté SL(E). Il s'agit d'un groupe de Lie classique, c'est-à-dire d'un sous-groupe fermé de GL(E). Géométriquement, un opérateur appartient à SL(E) ssi il préserve le volume de Lebesgue de E. Son algèbre de Lie est exactement l'ensemble des opérateurs u de trace nulle, noté
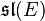
Sur un ouvert U de E, un champ de vecteurs X est une application
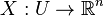
- c'(t) = X(c(t)) (1).
Le flot de X est la famille de difféomorphismes ft qui envoient x sur c(t), où c est la solution de (1) avec comme condition initiale c(0)=x. Le flot est défini localement. On introduit la divergence de X
- div(X)(x) = Tr(dX(x))
où dX(x) désigne la différentielle de X en x, qui est un opérateur sur E. Le flot ft préserve le volume de Lebesgue ssi la divergence est nulle. Plus précisément, pour tout ouvert Ω dont l'adhérence est incluse dans U,
-
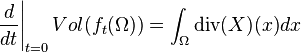
(Cette égalité permet d'étendre la définition de la divergence, par exemple sur des variétés orientées en présence de formes volumes. Voir divergence (mathématiques).)
Forme de Killing
Si
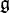
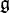
- ad(X)(Y) = [X,Y].
La forme de Killing sur
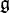
-
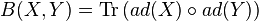
Les automorphismes de l'algèbre de Lie
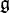
Soit G un groupe de Lie (par exemple, un sous-groupe fermé de GL(E)). Par définition, son algèbre de Lie est l'espace des champs de vecteurs sur G invariants à gauche, muni du crochet de Lie [,] (commutateur de champs de vecteurs). La forme de Killing associée B définit une métrique pseudo-riemannienne bi-invariante sur G. Si la forme de Killing B est définie positive, alors la métrique associée est une métrique riemannienne à courbure positive. Le théorème de Meyers implique que G est compact. D'autres liens existent.
Produit scalaire canonique
Soit
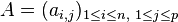
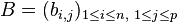
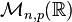
On dispose ainsi d'une écriture agréable du produit scalaire canonique sur l'espace Rnp.
Si H est un espace de Hilbert de dimension finie, la transposée d'un opérateur u sur H est un opérateur sur H. On définit alors le produit scalaire sur l'espace
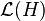
-
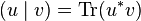
Avec cette définition, il apparait clairement que les opérateurs symétriques et les opérateurs antisymétriques forment deux sous-espaces orthogonaux de
Laplacien
Soit U un ouvert d'e l'espace vectoriel réel Rn contenant 0, et soit
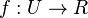
-
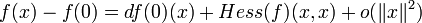
Par définition, le laplacien de f en 0 est la trace de la hessienne :
Les fonctions de classe C2 de laplacien nul sont dites harmoniques. Nécessairement analytiques, ces fonctions interviennent notamment en analyse complexe et en analyse fonctionnelle. En particulier, les fonctions de laplacien nul sont les solutions du problème de Dirichlet qui est la recherche des extrémales de l'énergie de Dirichlet.
Par ailleurs, la définition du Laplacien se généralise en géométrie différentielle pour des fonctions sur des variétés riemanniennes, mais aussi pour des objets plus généraux, comme par exemple les formes différentielles. Y compris dans ce cadre plus général, la définition peut être donnée par des traces de formes bilinéaires. Les formes de laplacien nul sont appelées harmoniques, et la théorie de Hodge en montre l'importance.
Termes de courbure
Etant donné une surface orientée lisse S de l'espace euclidien R3, la courbure moyenne de S en x est la moyenne des deux courbures principales de S en x. Formellement, ces courbures sont les valeurs propres d'une forme quadratique sur le plan tangent TxS, appelée la seconde forme fondamentale de S en x, notée IIx. La courbure moyenne de S en x est
-
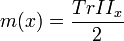
La définition de la courbure moyenne s'étend aux sous-variétés lisses N des variétés riemanniennes. Sa valeur en x n'est plus un scalaire mais un vecteur orthogonal à TxN, qui se définit encore au moyen de traces. Les sous-variétés de courbure moyenne nulle sont appelées minimales et sont les extrémales du volume riemannien.
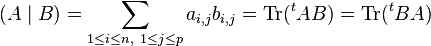
![\Delta f(0)=Tr [Hess(f)(0)]=\sum_{i=1}^n \frac{\partial^2f}{\partial x_i^2} (0)](https://static.techno-science.net/illustration/Definitions/autres/5/511859fb04ef9f5289b6a7e9295aaf25_1e7a5dc02acfeb97810cbf4d7167aa5c.png)

















































