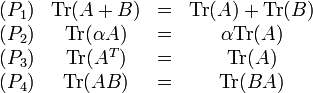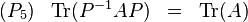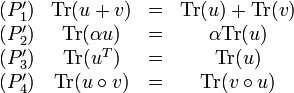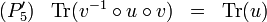Trace (algèbre) - Définition

Introduction

En algèbre linéaire, la trace d'une matrice carrée A est définie comme la somme de ses coefficients diagonaux, notée Tr(A). La trace peut être vue comme une forme linéaire sur l'espace vectoriel des matrices. Pour toutes matrices A et B, Tr(AB)=Tr(BA).

Si E est un espace vectoriel de dimension finie sur un corps K, alors il existe une unique application linéaire Tr sur l'espace des opérateurs de E, vérifiant Tr(uv)=Tr(vu) et Tr(Id)=dim E. Le scalaire Tr(u) s'appelle la trace de l'opérateur u, et vaut la trace de la matrice représentant u dans une base quelconque de E. Plus généralement, sur une algèbre A, une trace est une forme linéaire λ telle que λ(ab) = λ(ba). Cette définition se rencontre en particulier dans l'étude des algèbres de von Neumann, qui sont des algèbres d'opérateurs sur des espaces de Hilbert.

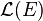
Parmi les applications,

- En algèbre linéaire, la trace d'un opérateur u est la somme de ses valeurs propres comptées avec multiplicité. Par exemple, la trace d'une rotation de R3 est 1 + 2cos(θ) et fournit donc l'angle de rotation θ.

- En théorie de Galois, la trace est à l'origine de la définition de la forme trace. Cette forme est aussi utilisée en théorie algébrique des nombres, par exemple pour définir le discriminant d'un anneau d'entiers algébriques.

- Dans la théorie des représentations, la trace d'une représentation est son caractère. Par exemple, pour une représentation d'un groupe fini, son caractère permet de comprendre sa décomposition en somme directe de représentations irréductibles. Cette théorie permet de mieux comprendre la structure d'un groupe. En conséquence, on retrouve l'utilisation de cet outil dans la démonstration de théorèmes sur le sujet, comme par exemple celui de Burnside sur un groupe résoluble ou celui sur le problème de Burnside.

- Dans l'étude des groupes de Lie, et toujours en rapport avec la théorie des représentations, la trace permet de définir la forme de Killing, qui est une forme quadratique sur l'algèbre de Lie correspondante. Le critère de Cartan en montre l'importance. Par exemple, la forme de Killing est définie négative ssi la composante neutre est compact (théorème de Meyers).

- En calcul différentiel, la trace apparait comme la différentielle du déterminant en l'identité. La trace intervient dans la définition de la divergence d'un champ de vecteurs, qui mesure le défaut à ce que son flot préserve le volume.

Dans tout l'article on considère des matrices à coefficients dans un corps .

Définition

Trace d'une matrice carrée

Étant donnée une matrice carrée à coefficients dans un corps K ou dans un anneau A, sa trace, notée Tr(A), est la somme de ses coefficients diagonaux :

.

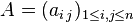
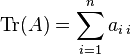
La trace est un scalaire. Pour toutes matrices carrées A et B (de même ordre) et pour tout scalaire , les propriétés suivantes sont vérifiées :

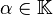
A^T désigne la transposée de A, et AB le produit matriciel de A et de B.

La propriété 4 a pour corolaire important l'égalité suivante, valable pour toute matrice carrée A et pour toute matrice inversible P de même ordre :

Autrement dit, la trace est un « invariant de similitude » pour les matrices carrées d'ordre donné. Ainsi, la trace est une forme linéaire sur l'espace vectoriel des matrices carrées d'ordre n (propriétés 1 et 2), invariante par transposition (propriété 3) et par similitudes.

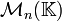
Inversement, toute forme linéaire sur l'espace invariante par similitude est proportionnelle à la trace.

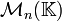
Trace d'un endomorphisme

Sur un espace vectoriel E de dimension finie n, la trace d'un endomorphisme , notée Tr(u), est définie comme la trace de la représentation matricielle de u relativement à une base préalablement fixée de E. La propriété (P5) ci-dessus montre que cette définition ne dépend pas du choix arbitraire de .

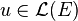
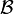
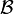
En effet, étant données deux bases et , est introduite la matrice de passageP de la base à la base . Les matrices A et A' représentant u respectivement dans et vérifie la relation dite « de changement de base » : A' = P ^{− 1}AP. Par la propriété (P5), Tr(P ^{− 1}AP) = Tr(A), donc Tr(A') = Tr(A).

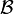
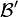
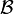
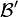
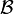
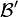
Les propriétés suivantes sont vérifiées pour tous endomorphismes et pour tout scalaire .

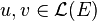
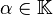
De plus, si (c'est-à-dire que v est un automorphisme), alors :

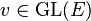
Autrement dit la trace est une forme linéaire sur l'espace vectoriel , invariante par transposition et par conjugaison.

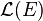
Trace d'une forme quadratique

Soit (E,g) un espace euclidien de dimension finie. Pour toute forme quadratique q sur E, il existe un opérateur symétrique A sur (E,g) tel que

q(v) = g(v,Av).

La trace de A est appelée trace de la forme quadratique q par abus de langage. Sa définition dépend explicitement du choix de la métrique euclidienne g.