Triangle de Pascal - Définition

Construction

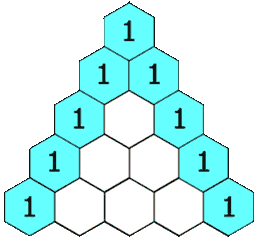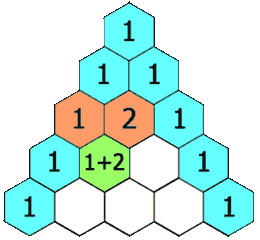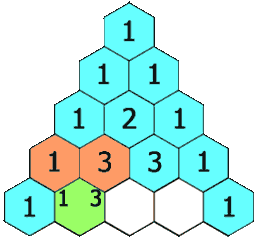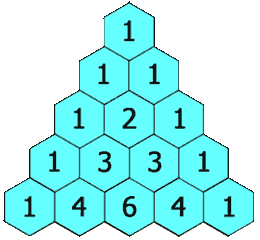
Le triangle de Pascal se construit de la manière suivante : placer 1 au sommet de la pyramide, puis 1 et 1 en dessous, de part et d'autre. Les extrémités des lignes sont toujours des 1, et les autres nombres sont la somme des deux nombres directement au-dessus.

Combinatoire

En écrivant la formule de Pascal,

pour tous entiers i et j tels que 0 < j < i,

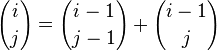
nous remarquons que le coefficient de la ligne i et colonne j s'obtient en ajoutant les coefficients de la ligne i - 1 et colonne j - 1 et de la ligne i - 1 et colonne j. De plus nous savons que

.

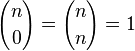
Nous en déduisons une méthode de construction du triangle de Pascal :

• nous plaçons dans la colonne 0 des 1 à chaque ligne, et des 1 à chaque entrée de la diagonale,
• en partant du haut et en descendant, nous complétons le triangle en ajoutant deux coefficients adjacents d'une ligne, pour produire le coefficient de la ligne inférieure, en dessous du coefficient de droite.

Suivant le schéma suivant, il est simple de ne pas se tromper :

      A  +  B           ||         (A+B)      

Matricielle

Facile à construire à partir des factorielles, il est possible de représenter le triangle de Pascal à l'aide de l'exponentielle d'une matrice : le triangle est le résultat de l'exponentielle d'une matrice dont la sous-diagonale contient 1, 2, 3, 4…, zéro ailleurs.

Informatique

Un algorithme, en langage formel, de construction du triangle de Pascal peut se présenter comme suit, en utilisant la relation de récurrence entre coefficients binomiaux :

      Variables:      Tableau de 1 à X de tableau de 1 à X d'entiers c (tableau bidimensionnel)      Entiers i, j, n, x      

      n ← 10    (* n est inférieur ou égal à la taille X utilisée dans le tableau c *)      c[0][0] ← 1            pour i de 1 à n faire           c[i][0] ← 1           pour j de 1 à i-1 faire                c[i][j] ← c[i-1][j-1] + c[i-1][j]           finpour           c[i][i] ← 1      finpour      

Généralisations

La formule du binôme généralisé est une importante généralisation du triangle de Pascal, car elle permet de manipuler des nombres complexes dans la base, tout comme d'utiliser des exposants complexes.

Le triangle de Pascal se généralise aisément à des dimensions supérieures. La version tridimensionnelle s'appelle la pyramide de Pascal.