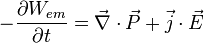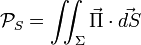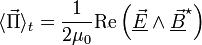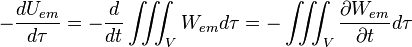Vecteur de Poynting - Définition

Introduction

Le vecteur de Poynting, noté Π, S, ou encore R est un vecteur dont la direction indique, dans un milieu isotrope, la direction de propagation d'une onde électromagnétique et dont l'intensité vaut la densité de puissance véhiculée par cette onde. Le module de ce vecteur est donc une puissance par unité de surface, c'est-à-dire un flux d'énergie.

Expression générale du vecteur de Poynting

Soient E et B le champ électrique et le champ magnétique. Alors, le vecteur de Poynting est défini par :

,

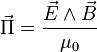
où μ est la perméabilité du vide. Dans un matériau de perméabilité magnétique μ quelconque, il convient de prendre en compte l'excitation magnétique H définie par la relation B = μ H. L'expression plus générale du vecteur de Poynting est donc :

.

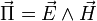
Puissance électromagnétique traversant une surface Σ

Une conséquence du théorème de Poynting est que la puissance électromagnétique traversant une surface Σ est donnée par le flux du vecteur de Poynting à travers cette surface.

Moyenne temporelle en notation complexe

Dans le cas d'une onde électromagnétique plane progressive harmonique, on a et  ; on peut donc associer des grandeurs complexes aux champs et en posant et , où i est le nombre complexe tel que i² = − 1.

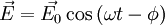
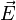
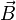
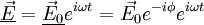
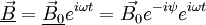
La moyenne temporelle du vecteur de Poynting vaut alors

,

où désigne le conjugué de .

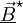
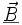
Équation de l'énergie d'un champ électromagnétique

Soit U_em l'énergie du champ électromagnétique :

avec W densité volumique d'énergie (quantité d'énergie par unité de volume)

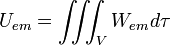
On définit la quantité d'énergie quittant un volume τ pendant un temps δt :

Soit , vecteur flux d'énergie du champ. D'après le théorème de Green-Ostrogradsky (Théorème de flux-divergence) on peut dire que le flux sortant du volume V est :

avec vecteur normal à la surface. Σ du volume, orienté vers l'extérieur

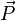
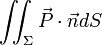
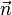
On peut expliciter la perte d'énergie du volume de la manière suivante :

• Pertes dues aux "frottements" des charges mobiles (voir Loi Ohm Locale, effet Joule).
• Pertes dues au rayonnement électromagnétique sortant du volume.

On peut donc dire que :

+ travail fourni par le champ à la matière

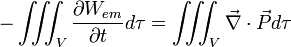
Calculons ce travail :

(on voit facilement que la force magnétique ne travaille pas.)

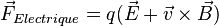
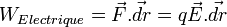
Passons à la puissance fournie par le champ :

pour une charge.

On est dans le cas de N charges :

or

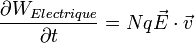
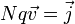
donc

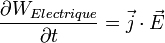
Cette perte de puissance est égale à la perte d'énergie du champ par unité de temps et de volume donc on écrit finalement :

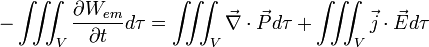
Donc finalement on a :

eq. de l'énergie du champ électromagnétique