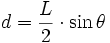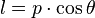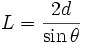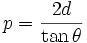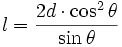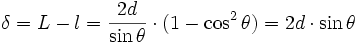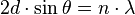Interférences par une lame d'air - Définition

L'interférence par une lame d'air est un phénomèe d'interférence obtenu avec un interféromètre de Michelson. Il s'agit d'une simplification du phénomène d'interférence par une couche mince d'indice de réfraction différent de 1.

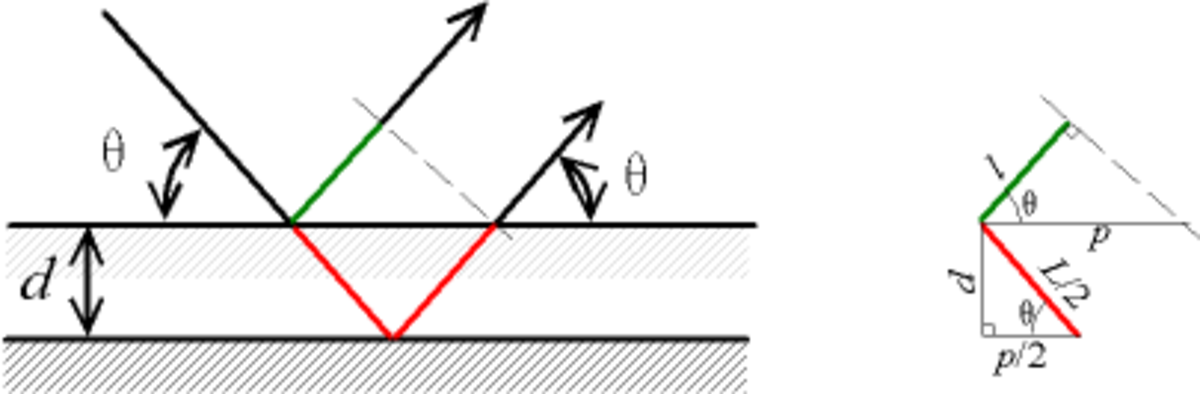
Si on laisse les deux miroirs perpendiculaires aux axes de l'appareil mais que l'on en écarte un d'une distance d, on provoque un phénomène similaire appelé " interférence par une lame d'air " : tout se passe comme si l'on avait un miroir semi-transparent devant un miroir, espacés de d.

Les rayons sont réfléchis de manière symétrique.

Conditions d'interférence constructive

Si l'on appelle :

• θ le complémentaire de l'angle d'incidence (c'est-à-dire l'angle entre le rayon et la surface)
• L le chemin parcouru par le rayon entre les deux miroirs ;
• l le chemin parcouru par le rayon réfléchi par le premier miroir entre la réflexion et le plan du front d'onde du rayon émergeant de l'entre-miroirs ;
• p la distance séparant le point d'entrée et le point de sortie du rayon parcourant l'inter-miroirs ;

alors on a deux triangles rectangles, qui permettent de déterminer par les relations trigonométriques que :

soit

La différence de chemin optique δ entre ces deux rayons est donc

Les rayons étant parallèles, ils se rencontrent " à l'infini " (c'est-à-dire après quelques mètres à l'échelle optique). Les interférences seront constructives si le déphasage entre les ondes est un multiple de 2π radians, c'est-à-dire si la différence de marche est un multiple de la longueur d'onde λ. On verra donc un maximum d'intensité dans les directions θ vérifiant :

où n est un nombre entier appelé " ordre d'interférence ".