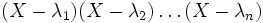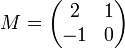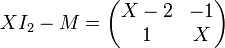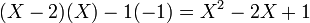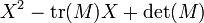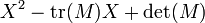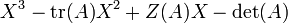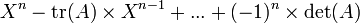Polynôme caractéristique - Définition
En algèbre linéaire, à toute matrice carrée ou à tout endomorphisme d'un espace vectoriel de dimension finie est associé un polynôme appelé polynôme caractéristique.
Il renferme d'importantes informations sur la matrice ou sur l'endomorphisme, comme ses valeurs propres, son déterminant et sa trace.
Motivation
Étant donné une matrice carrée M d'ordre n, nous voulons trouver un polynôme dont les racines sont précisément les valeurs propres de M.
Si M est une matrice diagonale ou plus généralement une matrice triangulaire, alors les valeurs propres de M, λ1, ..., λn sont les coefficients diagonaux de M et nous pouvons définir le polynôme caractéristique comme étant
Nous remarquons que ce polynôme est le déterminant det(XIn − M) où In est la matrice unité.
Pour une matrice quelconque M, nous pouvons voir que si λ est une valeur propre de M, alors il existe une colonne propre V non nulle tel que MV = λV, soit (λIn-M)V = 0 (où In est la matrice unité.) Puisque V est non nulle, cela implique que la matrice λIn-M est singulière, et donc a son déterminant nul. Nous venons de démontrer que les valeurs propres de M sont des zéros de la fonction λ ? det(λ·In − M) ou des racines du polynôme det(XIn − M).
Définition formelle
Soit M une matrice carrée d'ordre n à coefficients dans un anneau commutatif. Le polynôme caractéristique de M, noté pM(X), est le polynôme défini par
où In désigne la matrice unité d'ordre n. pM est bien un polynôme puisque le déterminant d'une matrice est défini comme une somme de produits.
- Remarque
- Certains auteurs définissent le polynôme caractéristique comme étant det(M − XIn), mais cela n'a aucune importance puisque les deux polynômes diffèrent seulement d'un signe. Nous avons choisi l'autre définition afin que le polynôme caractéristique soit unitaire.
Exemple
Supposons que nous voulions déterminer le polynôme caractéristique de la matrice
Nous devons calculer le déterminant de la matrice
et celui-ci est égal à
Ce dernier polynôme est le polynôme caractéristique de M.
On peut aussi utiliser la formule
pour le cas d'une matrice de dimension (2,2).
Propriétés
Le polynôme pM(t) est unitaire (son coefficient dominant est égal à 1) et son degré est égal à n. La propriété la plus importante des polynômes caractéristiques est que les valeurs propres de M sont exactement les racines du polynôme pX(X) (une implication a été démontrée dans le paragraphe Motivation.) Le coefficient constant pM(0) est égal à (-1)n fois le déterminant de M, et le coefficient de Xn-1 est égal à l'opposé de la trace de M.
Pour une matrice M d'ordre 2, le polynôme caractéristique s'exprime simplement comme
où tr(M) représente la trace de la matrice de M et det(M) le déterminant de M.
Pour une matrice A d'ordre 3, le polynôme caractéristique s'exprime simplement comme
où
-
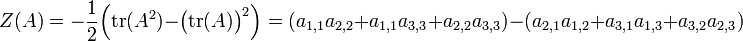
avec ai,j l'élèment en position (i, j) dans la matrice A.
De façon générale, à l'ordre n, seuls les termes d'ordre maximum sont intéressants, et on a:
Le théorème de Cayley-Hamilton affirme qu'en remplaçant X par M dans pM(X), on obtient la matrice nulle: pM(M) = 0. Ce qui signifie que le polynôme caractéristique est un polynôme annulateur de M. Par conséquent, il est possible de démontrer que le polynôme minimal divise le polynôme caractéristique de M.
Deux matrices semblables ont le même polynôme caractéristique. La réciproque n'est pas vraie en général : deux matrices ayant même polynôme caractéristique ne sont pas nécessairement semblables.
La matrice M et sa transposée ont le même polynôme caractéristique.
Une matrice M est semblable à une matrice triangulaire si et seulement si son polynôme caractéristique peut être complètement décomposé en produit de facteurs de degré un à coefficients dans

En fait, M est même semblable à une matrice de Jordan dans ce cas.
Matrice compagnon
Soit
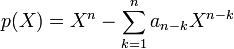

qui admet p(X) comme polynôme caractéristique (et polynôme minimal), est appelée matrice compagnon du polynôme (ou selon certains ouvrages, sa transposée). Une des méthodes utilisées en calcul numérique pour calculer des valeurs approchées des racines d'un polynôme est d'en construire la matrice compagnon puis de calculer des valeurs approchées des valeurs propres de cette matrice à l'aide d'une méthode itérative.