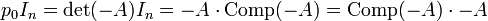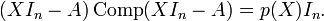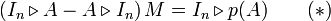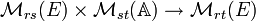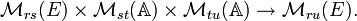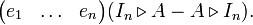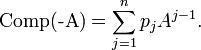Théorème de Cayley-Hamilton - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En algèbre linéaire, le théorème de Cayley-Hamilton (qui porte les noms des mathématiciens Arthur Cayley et William Hamilton) affirme que tout endomorphisme d'un espace vectoriel de dimension finie sur un corps quelconque annule son propre polynôme caractéristique.
En termes de matrice, cela signifie que :
si A est une matrice carrée d'ordre n et si
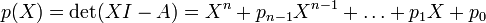
est son polynôme caractéristique (polynôme d'indéterminée X), alors en remplaçant formellement X par la matrice A dans le polynôme, le résultat est la matrice nulle :
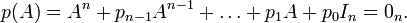
Le théorème de Cayley-Hamilton s'applique aussi à des matrices carrées à coefficients dans un anneau commutatif quelconque.
Un corollaire important du théorème de Cayley-Hamilton affirme que le polynôme minimal d'une matrice donnée est un diviseur de son polynôme caractéristique.
Motivation
Ce théorème possède deux familles d'utilisation :
- Il permet d'établir des résultats théoriques, par exemple pour calculer le polynôme caractéristique d'un endomorphisme nilpotent.
- Il autorise aussi des simplifications puissantes dans les calculs de matrices. L'approche par les polynômes minimaux est en général moins coûteuse que celle par les déterminants.
On trouve ce théorème utilisé dans les articles sur les polynômes d'endomorphisme, endomorphismes nilpotents, et plus généralement dans la théorie générale des matrices
Démonstration
Une preuve
Quelle que soit la matrice
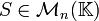
![\mathbb{K}[X]](https://static.techno-science.net/illustrationWebp/Definitions/autres/a/a54a58150f8fbfa21e4e47bea7551681_74473e1ff482d8b2fb4406e56cad5749.png)
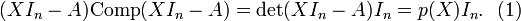
Partons de (1), en écrivant
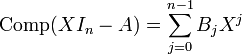
avec
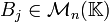
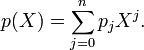
On peut développer le produit (XIn − A)Comp(XIn − A) :
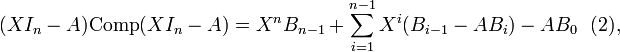
qui est identique à
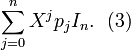
Les polynomes (2) et (3) sont égaux. Par conséquent,
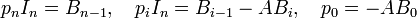
Il vient alors un télescopage :
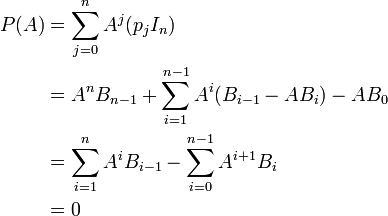
La preuve ne consiste pas en une substitution de X par A dans des égalités de polynômes, mais à une identification de leurs coefficients.
Une variante
On peut également aligner des idées abstraites.
Commençons par introduire un morphisme d'évaluation approprié à la résolution du problème. Tout d'abord,
![\mathbb{K}[A]](https://static.techno-science.net/illustrationWebp/Definitions/autres/d/dd8ed67f088d3d54e206442208df1704_2ea0306c91b50668a5e758d81a709a2d.png)
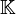
![\mathbb{K}[X] \to \mathbb{K}[A]](https://static.techno-science.net/illustrationWebp/Definitions/autres/c/cd1fd81afb8fe40a01176310d6a92d38_6db8f46123b66c1d064e14a87ad47174.png)
![\mathcal{M}_n(\mathbb{K}[X]) \to \mathcal{M}_n(\mathbb{K}[A])](https://static.techno-science.net/illustrationWebp/Definitions/autres/a/a8b6a24e6181b8e629c160788c40ae3a_e3d7a665449f4f2b898fd6868e93dab7.png)
Une notation auxiliaire nous sera utile : pour deux matrices carrées (n,n) notées C = (cij) et D = (dij), on notera
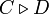
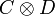
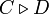
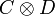
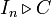
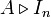
Cette notation posée, appliquons le morphisme d'évaluation à la relation :
On obtient une relation
dans laquelle M est une certaine matrice à coefficients dans
Ainsi on a écrit une formule juste, et on en pâtit : on n'a du coup pas fini, l'évaluation de XIn − A par une technique rigoureuse ne fournit pas 0 mais une bizarre matrice à coefficients matriciels.
Il faut une deuxième idée pour conclure. Elle consiste à remarquer que si
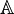
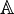
pour laquelle on a associativité si on veut calculer des produits à trois termes :
Appliquons cette notion à
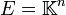
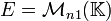
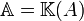
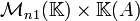
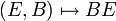
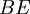
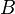
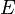
Multiplions à gauche la relation ( * ) par le vecteur ligne
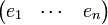
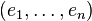
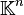
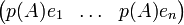
Si maintenant on utilise l'expression de gauche dans ( * ) et qu'on déplace les parenthèses par associativité de la multiplication matricielle un peu inhabituelle décrite ci avant, on est amené à calculer le produit :
Pour chaque indice j, on ne peut que constater que sa j-ème composante vaut :
-
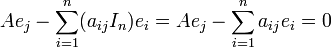
En multipliant ceci à droite par l'inoffensive matrice M et en comparant les deux expressions du produit, on conclut que pour tout indice j, p(A)ej = 0.
Et donc p(A) = 0.
Remarques additionnelles sur la démonstration
La preuve qui a été donnée évite la substitution de X par une matrice dans un contexte non commutatif, mais les manipulations effectuées sont quand même proches de cette idée : on a bien décomposé l'équation en composantes suivant les puissances de X, on a multiplié à gauche par Aj la composante qui était en facteur de Xj, et on a additionné tout ensemble. En fait, on a utilisé l'opération EvA définie en (5), sans supposer qu'il s'agisse d'un homomorphisme d'anneaux, de
![\mathcal{M}_n(\mathbb{K})[X]](https://static.techno-science.net/illustrationWebp/Definitions/autres/1/1c75e1dfa516ba1ba75c9d6c4a2dd3e3_771460fbfffb013aeb1be5c029edeb29.png)
Une autre observation est importante : la forme exacte du polynôme Comp(XIn − A) n'a aucune importance. Il y a donc quelque chose à exploiter ici, ce que n'ont pas manqué de faire les mathématiciens.
Soit M un anneau non commutatif ; on peut définir une division euclidienne d'un polynôme
![P\in M[X]](https://static.techno-science.net/illustrationWebp/Definitions/autres/2/2f475431ef51dd5b6c7f4932a34d5f60_035186efd08eaa430e175b045f16b623.png)
![Q, R\in M[X]](https://static.techno-science.net/illustrationWebp/Definitions/autres/c/ca177aeefd0bdb387d55f236c6d9782e_8c0db0af6dc32e3c9c05cd4517682952.png)
- P = BQ + R.
La démonstration est entièrement analogue à celle du cas scalaire. Si B = XIn − A, alors le reste R est de degré 0, et donc identique à une constante appartenant à M. Mais dans ce cas, en raisonnant exactement comme dans la démonstration du théorème de Cayley-Hamilton, on arrive à la conclusion
- EvA(P) = R.
Il s'ensuit que EvA(P) est nul si et seulement si P est divisible à gauche par XIn − A.
La démonstration du théorème de Cayley-Hamilton donne aussi une autre information : le polynôme Comp(XIn − A) est le quotient à gauche de p(X)In par tIn − A. Comme p(X)In et XIn − A appartiennent tous deux au sous-anneau commutatif K[A][X], la division à gauche se passe entièrement dans ce sous-anneau, c'est donc une division ordinaire. En particulier, les coefficients matriciels de Comp(XIn − A) sont des combinaisons linéaires de puissances de A. En d'autres termes, la matrice complémentaire d'une matrice A est un polynôme en A, ce qu'il n'est pas facile de déduire directement de la définition d'une matrice complémentaire. Mieux, on peut calculer explicitement ses coefficients à partir de ceux du polynôme caractéristique p(X), puisqu'il s'agit de faire une division euclidienne ordinaire, et on trouve
On aurait pu également obtenir cette relation directement à partir du théorème de Cayley-Hamilton, en vertu de l'identité
-
